数据结构：二叉平衡树

在学数据结构与算法的时候，二叉平衡树也就是AVL树是一个很重要的数据结构。下面我将由浅入深的讲解它。

什么是二叉平衡树

二叉平衡树又叫做AVL树为啥会有这么奇怪的名字呢？原因是为了纪念前苏联的两个科学家Adelse-Velskil和Landis，取其首字母 AVL 因此叫做AVL树。
它的全名是平衡二叉查找树，这里有二叉查找树，这是不是就说明它是和BST有关的呢
实际上平衡二叉查找树，就是树如其名 二叉，代表是二叉树，查找树，说明它是拥有和BST一样的性质，左<root<右。平衡代表任意一个节点的左右子树的高度差<=1
又被称为|平衡因子|<=1。
平衡因子：某节点的左⼦树与右⼦树的⾼度(深度)差即为该节点的平衡因子。（BF,Balance Factor）
这样我们就对二叉平衡树有了大致的了解，可以把它理解为一棵二叉查找树+平衡的性质。
AVL树一定是BST树，但BST树不一定是AVL树。

为什么会有二叉平衡树

AVL 树其实就是为了防止普通二叉搜索树（BST）变成“歪脖子树”而发明的。
普通 BST 的有着致命的缺陷，
普通 BST 在理想情况下查找、插入、删除都是O(logn)
因为树的高度接近 log n。
但是会有一种比较糟糕的插入顺序，插成一棵斜树了。

1\2\3\4\5

这已经不是树了，是链表，高度 = N，查找变成O(n)
那么这和线性搜索就没什么区别了
为了弥补这一缺陷，有了AVL树
AVL 树的好处在于AVL 树在每次插入、删除时都会主动检测平衡因子并通过旋转修复。它保证：任意节点的左右子树高度差≤1，所以树的高度最多是O(logn)
无论你插入数据的顺序多糟糕，都不会退化成链表。
那么使用AVL树进行查找，不管怎么插入，最终的最坏时间复杂度都是O（logn）
这大大的加快了速度。AVL树进行插入或者删除虽然有额外的开销，但仍是常数级，仍然是O（logn）

操作	普通 BST 最坏	AVL 树最坏
查找	O(n)	O(log n)
插入	O(n)	O(log n)
删除	O(n)	O(log n)

适用场景

因为插入或者删除有额外的开销，AVL树适用于查找操作频繁、更新操作较少时（查找性能更稳定）。

如何构造一棵二叉平衡树

建 AVL 树的核心思路就是：
按 BST 规则插入新值（先不管平衡）
插入后，从当前结点向上回溯，检查高度差
如果失衡（|左高 - 右高| > 1），根据插入位置类型，旋转修复。

插入节点

插入流程
假设我们从空树开始，依次插入数字：
第一步：正常 BST 插入
如果当前结点为空 → 直接创建新结点
如果 val < root->data → 插左子树
如果 val > root->data → 插右子树
第二步：更新高度
每次插入结束后，需要更新当前结点的高度
第三步：检查平衡因子避免失衡。
如果失衡，那么就根据情况进行旋转。
有以下四种选转情况：

类型	平衡因子方向	插入方向	旋转操作
LL	左高	插在左孩子的左边	右旋
RR	右高	插在右孩子的右边	左旋
LR	左高	插在左孩子的右边	左旋左孩子 + 右旋自己
RL	右高	插在右孩子的左边	右旋右孩子 + 左旋自己

AVLNode* insert(AVLNode*root,int k)//插入 建立一个平衡二叉树 
{if(root==NULL)//如果根指针为空，说明还没有创建第一个结点 {AVLNode*s=(AVLNode*)malloc(sizeof(AVLNode));//创建结点 s->data=k;//赋值 s->l=s->r=NULL;//左右孩子为空 s->h=0;root=s; //根指针指向 }//说明把一个数据放在了这个结点里面了 else if(k<root->data)//如果插入的k小于根节点中的数//就让它往左孩子中插入 {root->l=insert(root->l,k);///递归写法if(geth(root->l)-geth(root->r)>1)//root失衡 ，如果让左子树插入结点后出现失衡 {if(k<root->l->data)//说明放在了左侧 ，要右旋 {//root=LLrotation(root); } else{root=LRrotation(root);//lr}} }else if(k>root->data){root->r=insert(root->r,k);if(geth(root->r)-geth(root->l)>1)//root失衡 {if(k>root->r->data){//RRroot=RRrotation(root);} else{root=RLrotation(root);//LR}} }//因为在以上插入过程中root可能进行了调整，需要重新算一下高度root->h=maxx(geth(root->l),geth(root->r))+1;return root;
}

在这个过程中建一棵二叉排序树是容易的，难点在于旋转。
首先我们应该先判断平衡因子是否》1，然后再说是否要旋转。
举往左子树插入节点的例子,如果左子树的高度-右子树的高度大于1
那么就需要旋转，根据插入的情况，又分为左旋和右旋
如果插入的是左子树的左侧，那么就需要右旋
如果插入的是左子树的右侧，那么就需要左旋左孩子 + 右旋自己
跟上面的图中所写的是一致的。

if(geth(root->l)-geth(root->r)>1)//root失衡 ，如果让左子树插入结点后出现失衡 
{if(k<root->l->data)//说明放在了左侧 ，要右旋 {//root=LLrotation(root); } else{root=LRrotation(root);//lr}
} 

经过旋转调整后，AVL树不再失衡，也就是成为了真正意义上的AVL树。
需要注意的是AVL树的插入，是递归生成的，那么我们就需要要在插入一个节点后，不断的回溯判断，找到第一次失衡需要调整的节点，也就是插入一个节点x之后，x的可能有若干个长辈失衡，先去调整以离x最近的长辈为根的失衡子树—>最小失衡子树。
当明白大体的情况后，我们就来详细的讲一讲具体如何调整/或者说存在的四种失衡类型。
LL，RR,LR,RL
LL：失衡节点z的左孩子的左子树中插入了一个节点导致了z失衡
如图所示：

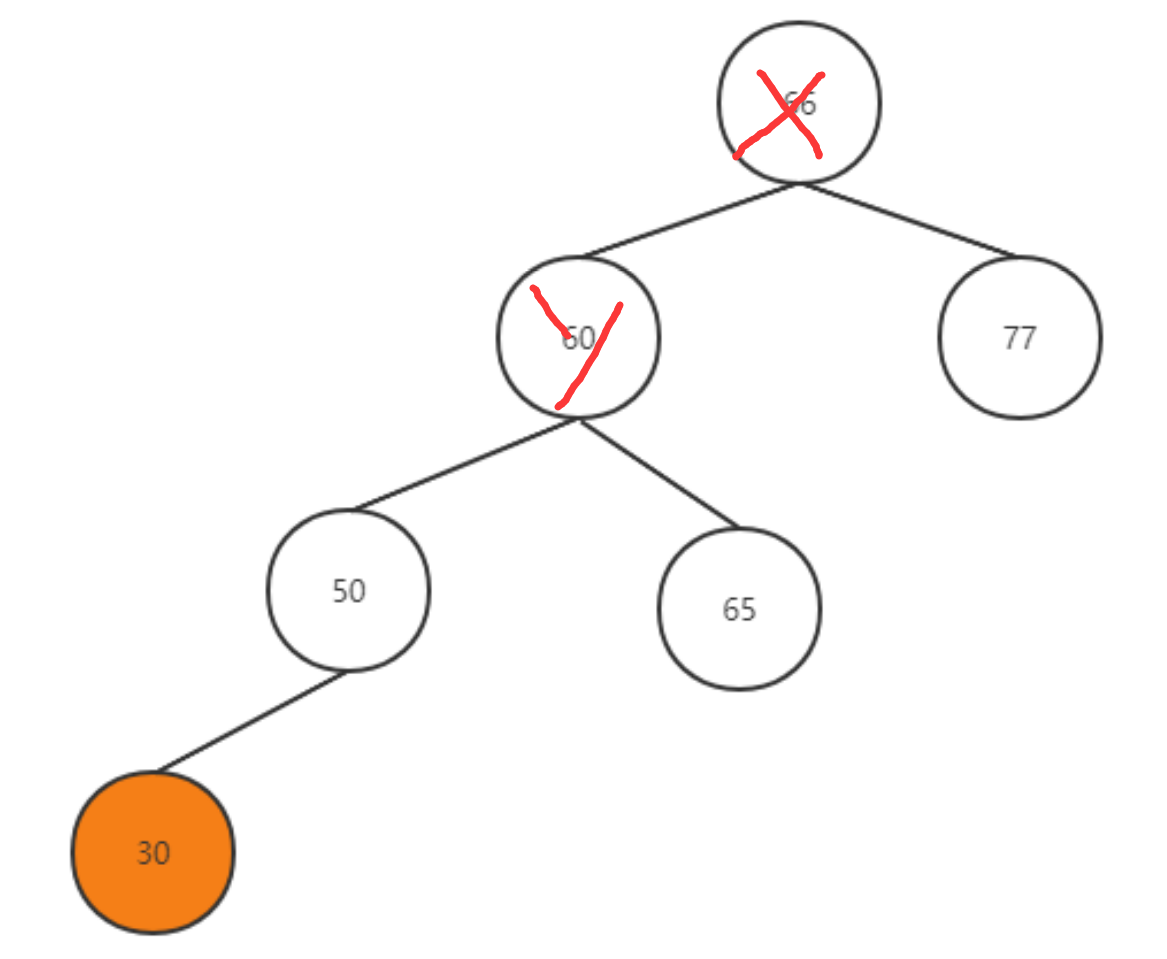
因为左边多了，那么我们肯定要想办法让它往右移动，也就是右旋

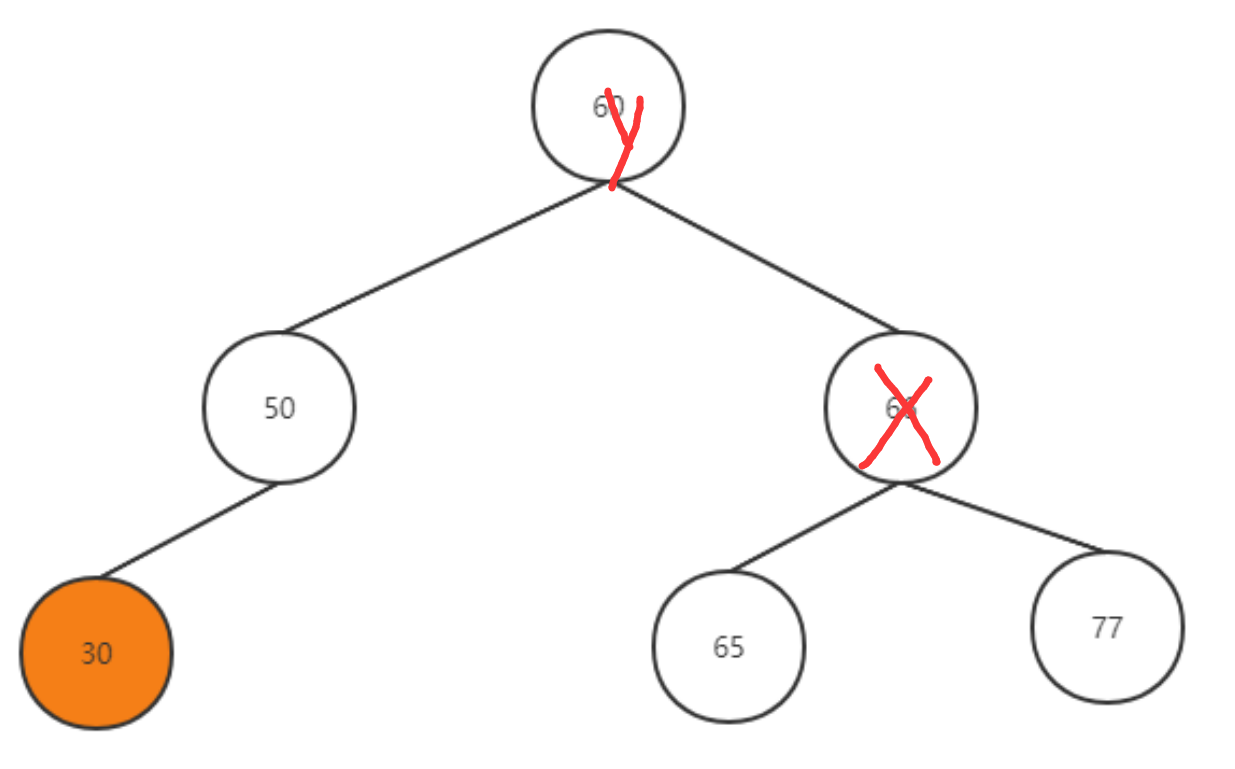
在旋转的过程中X变成了Y的右孩子，那么如果原来y有右孩子，需要把Y的右孩子放到旋转后X的左孩子的位置。
要注意在旋转的过程中指针的改变，这在写代码的时候十分重要。

AVLNode* LLrotation(AVLNode* x)
{AVLNode* y=x->l;x->l=y->r;//2y->r=x;//3x->h=maxx(geth(x->l),geth(x->r))+1;// 先求x的再求y的高度  y->h=maxx(geth(y->l),geth(y->r))+1;// return y;//1} 

RR ：失衡节点x的右孩子的右子树中插入了一个节点导致了x失衡

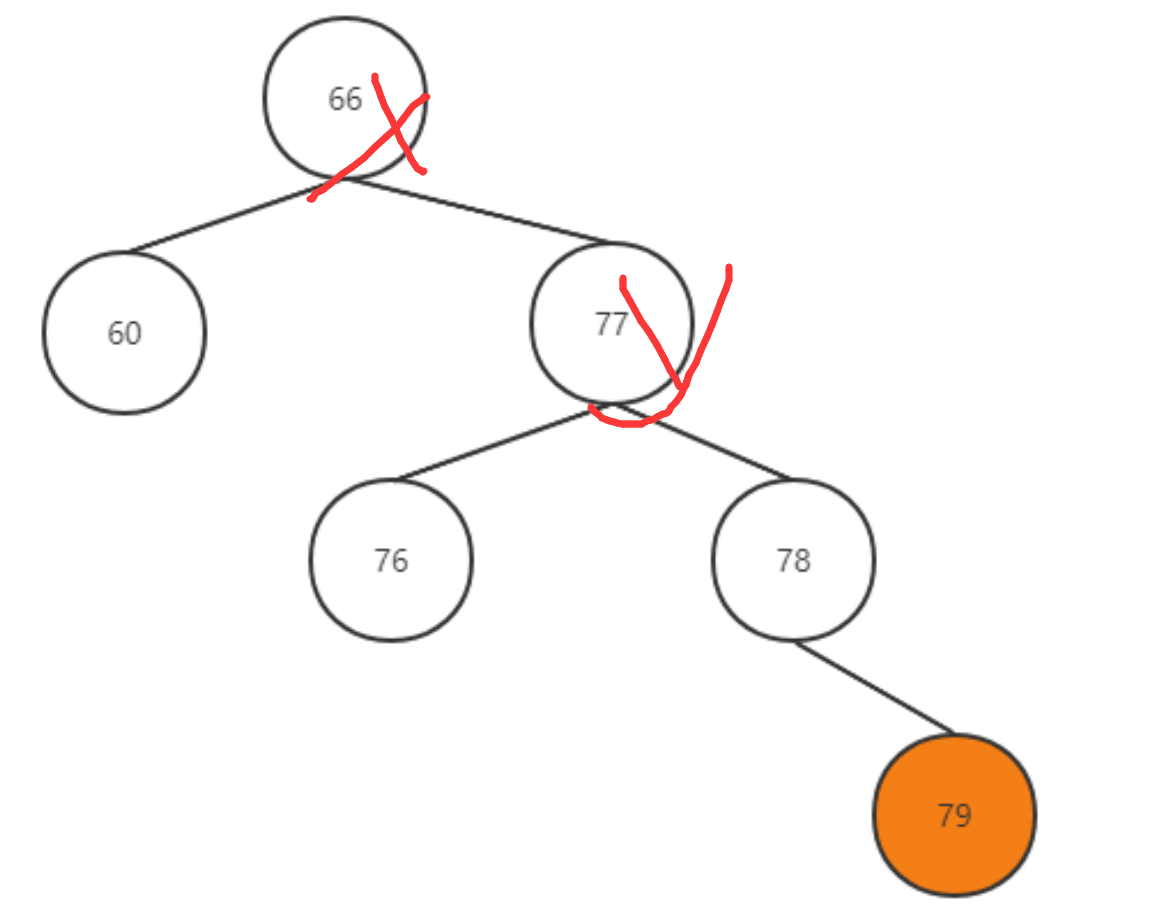
和LL类似无非是进行的是左旋因为右边多
经过右旋调整：

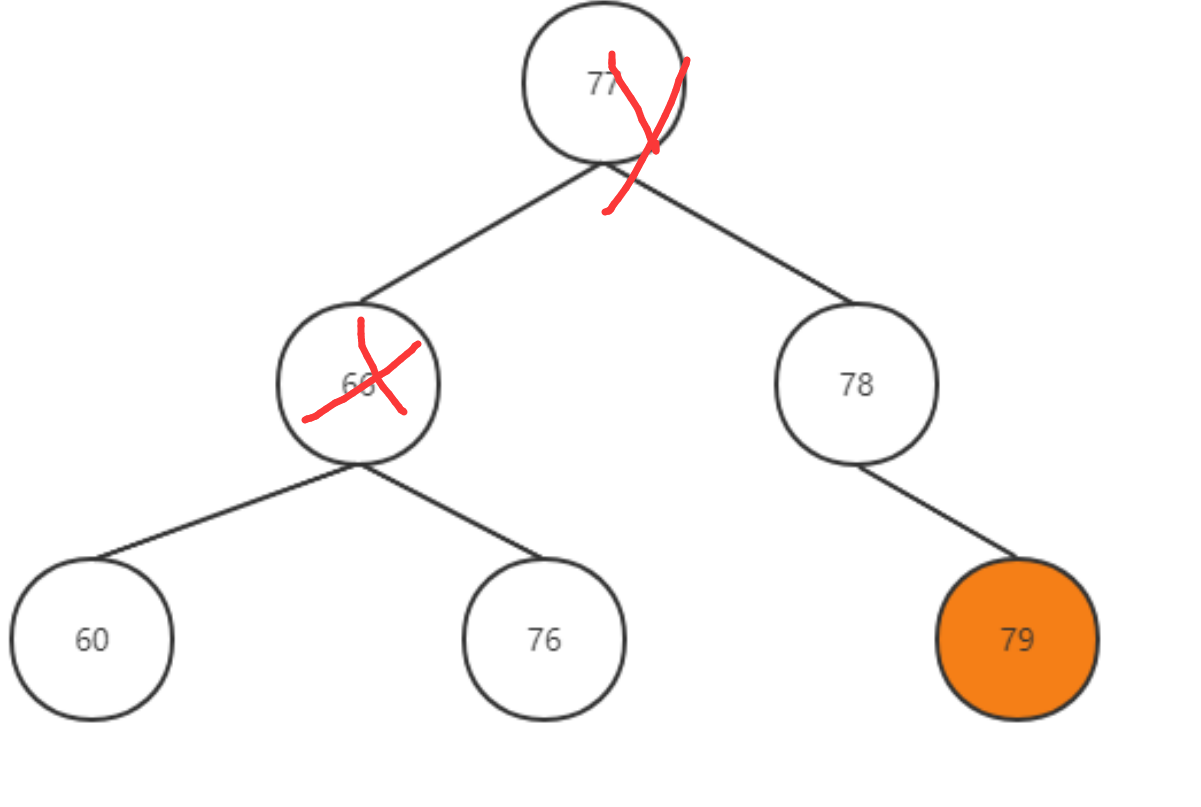
AVLNode* RRrotation(AVLNode* x)
{AVLNode* y=x->r;x->r=y->l;//2 y->l=x;//3x->h=maxx(geth(x->l),geth(x->r))+1;y->h=maxx(geth(y->l),geth(y->r))+1;return y;//1} 

LR 失衡节点x的左孩子的右子树中插入了一个节点导致了x失衡

经过旋转调整：

LR实际上，可以看成先对最小失衡子树的左孩子进行一个左旋

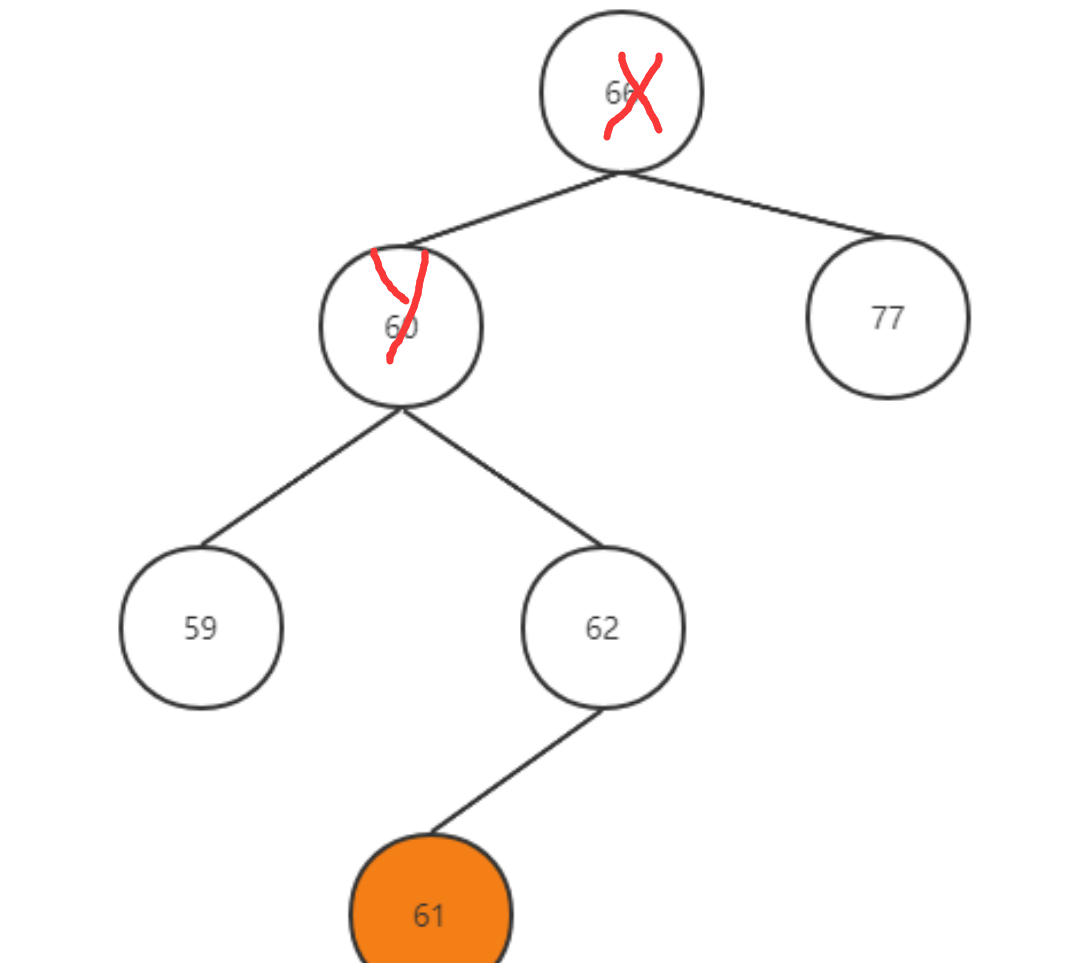
即需要先对Y进行左旋：

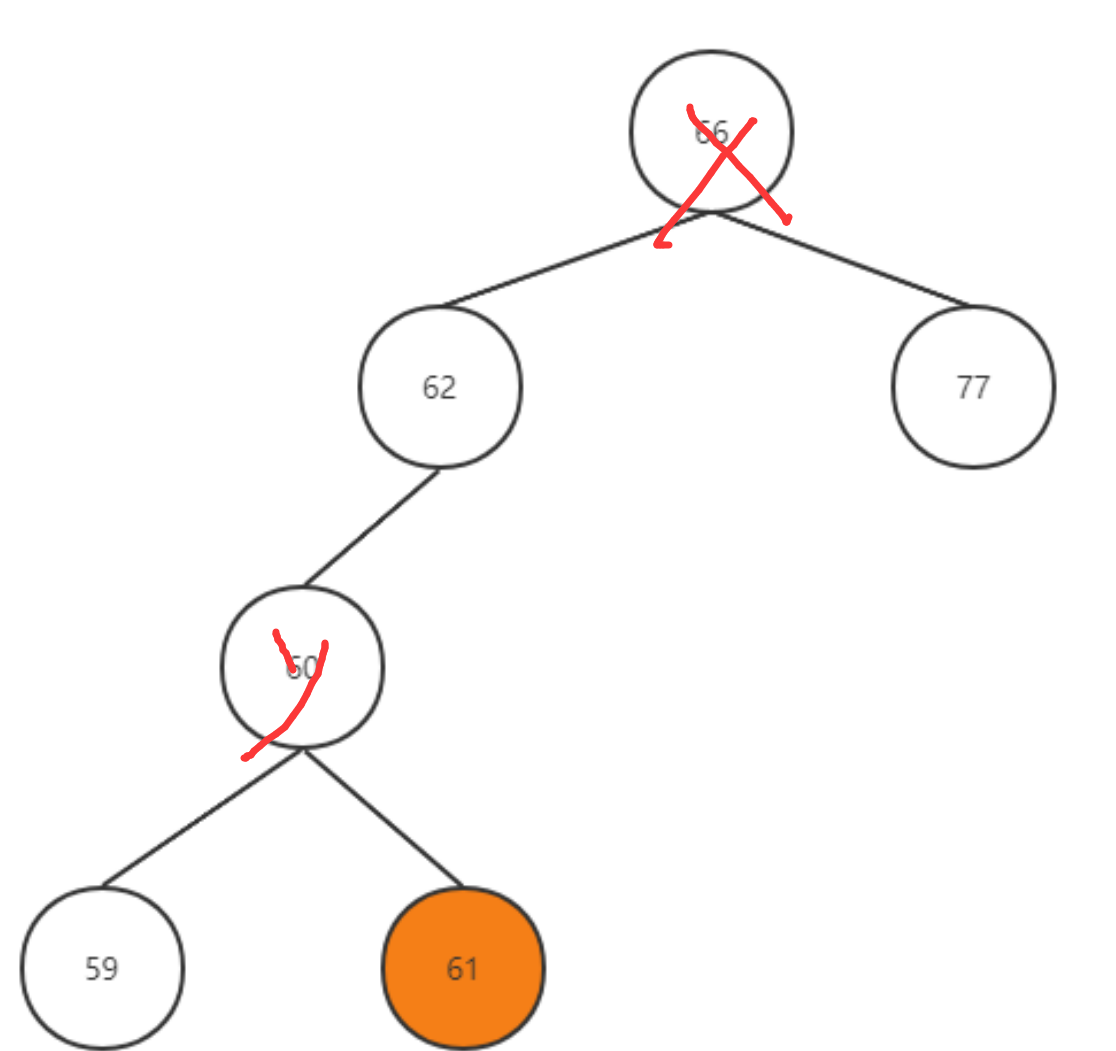
然后再对X进行右旋：

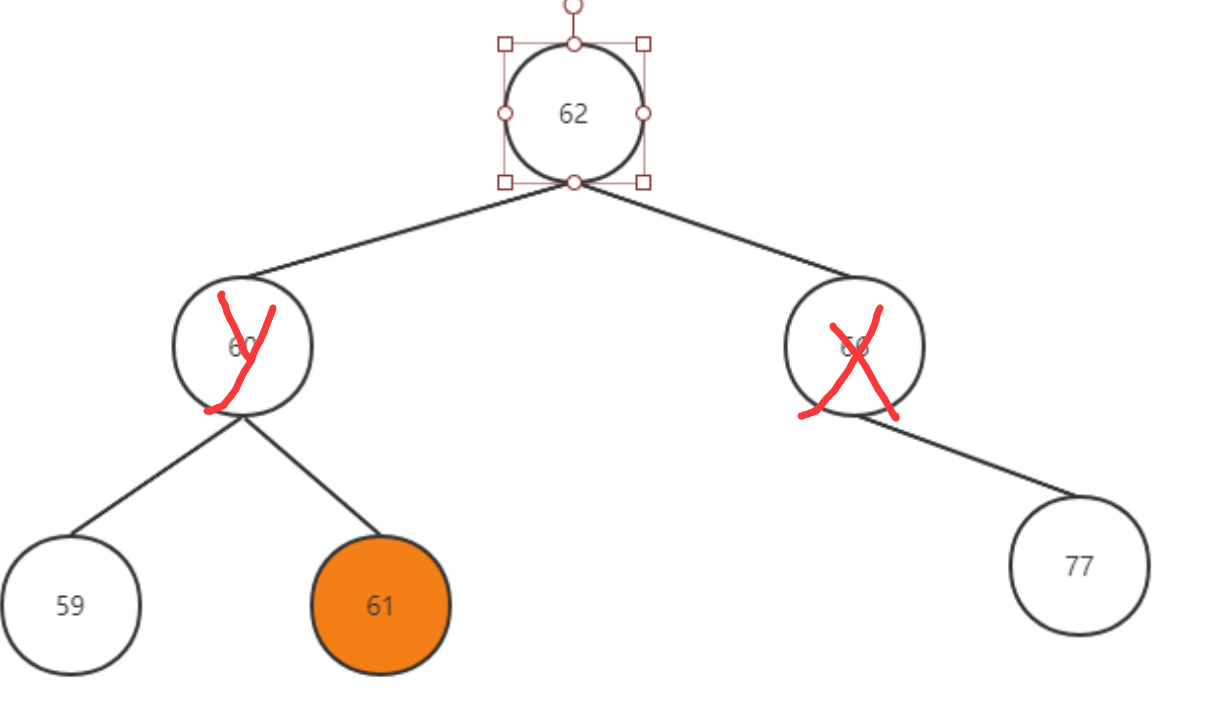
这样恰好使其平衡。
为啥需要这样子，为啥不能直接的左旋或右旋呢
这是因为BST 性质：中序遍历必须是递增的，平衡条件：任意节点左右子树高度差 ≤ 1，当插入新节点破坏了“平衡”，我们要通过旋转修复。但修复的时候，不能破坏 BST 的中序顺序。
拿这个场景举例：插入点在“左孩子 y 的右子树 z”

  x/
y\z

中序遍历：y < z < x
如果我们直接对 x 右旋：

y\x/
z

结果：中序顺序变成 y < x < z （z 被放错位置）
因此不能想当然的无脑进行左旋和右旋，而是要根据插入节点的位置灵活变通。
具体代码如下：

AVLNode*LRrotation(AVLNode* x)
{x->l=RRrotation(x->l);x=LLrotation(x);return x;
}

RL 失衡节点x的右孩子的左子树中插入了一个节点导致了x失衡

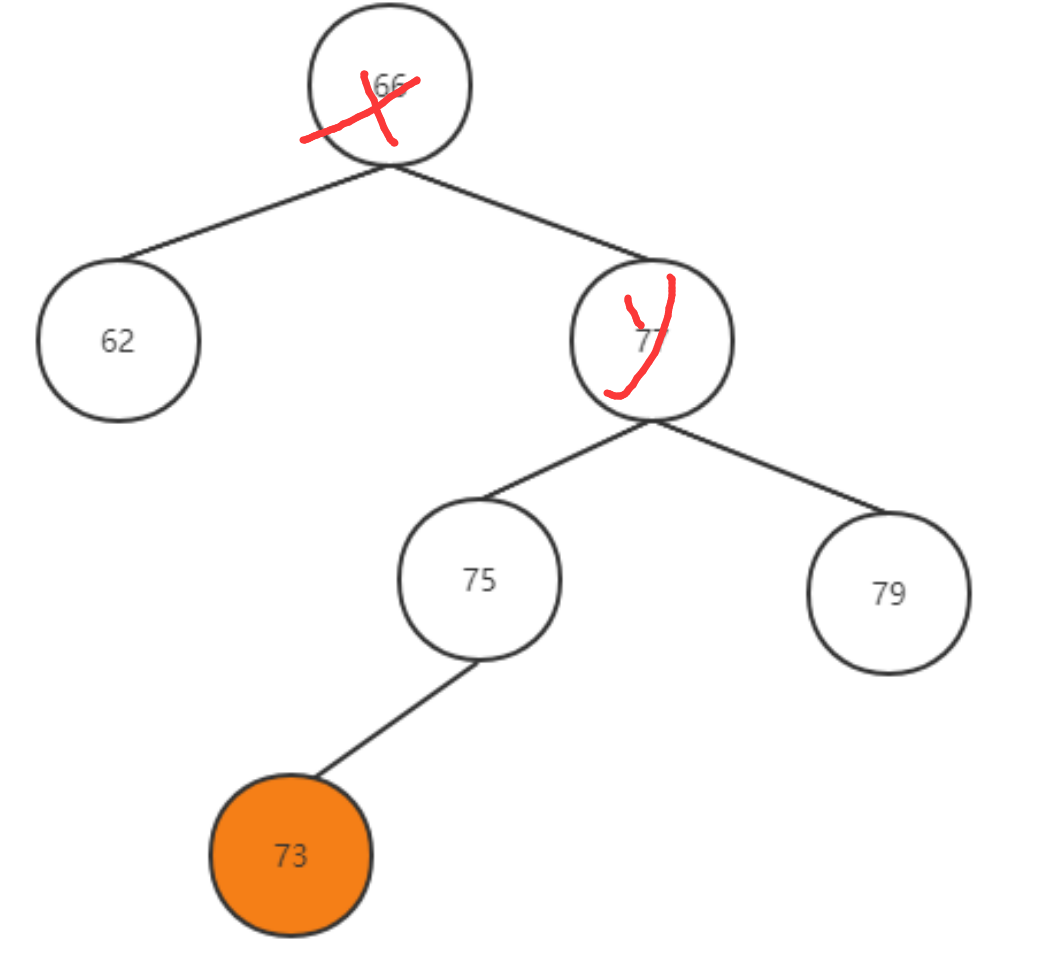
经过类似LR的处理得到：

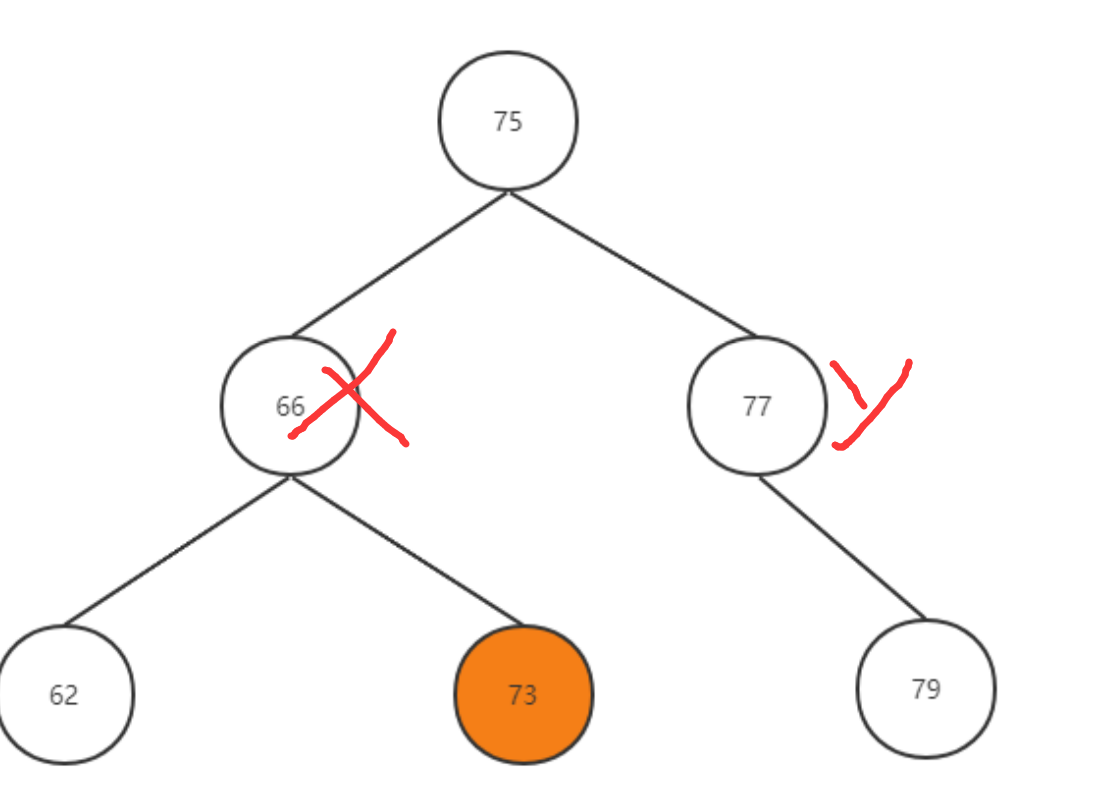
完整代码如下：

 AVLNode*RLrotation(AVLNode* x)
{x->r=LLrotation(x->r);x=RRrotation(x);return x;
}

这样我们就通过不断的插入，旋转平衡得出了一棵AVL树。
这里在插入的时候也要不断的统计高度，这样才能计算是否高度差>1，是否会导致失衡。
我们对节点高度的维护是通过它的左右孩子的高度来确定，
即，一个节点的高度是等于，它的左右节点的高度中的最大高度，然后+1.
每一个节点的初始高度为0

int geth(AVLNode*x)
{if(x==NULL){return 0;}else{return x->h;}
}
int maxx(int u,int v)
{if(u>v){return u;}else{return v;}
}
AVLNode* insert(AVLNode*root,int k)//插入 建立一个平衡二叉树 
{if(root==NULL)//如果根指针为空，说明还没有创建第一个结点 {AVLNode*s=(AVLNode*)malloc(sizeof(AVLNode));//创建结点 s->data=k;//赋值 s->l=s->r=NULL;//左右孩子为空 s->h=0;root=s; //根指针指向 }//说明把一个数据放在了这个结点里面了 else if(k<root->data)//如果插入的k小于根节点中的数//就让它往左孩子中插入 {root->l=insert(root->l,k);///递归写法if(geth(root->l)-geth(root->r)>1)//root失衡 ，如果让左子树插入结点后出现失衡 {if(k<root->l->data)//说明放在了左侧 ，要右旋 {//root=LLrotation(root); } else{root=LRrotation(root);//lr}} }else if(k>root->data){root->r=insert(root->r,k);if(geth(root->r)-geth(root->l)>1)//root失衡 {if(k>root->r->data){//RRroot=RRrotation(root);} else{root=RLrotation(root);//LR}} }//因为在以上插入过程中root可能进行了调整，需要重新算一下高度root->h=maxx(geth(root->l),geth(root->r))+1;return root;
}

总结AVL树的插入操作代码如下：

#include <stdio.h>
#include<stdlib.h>
typedef struct AVLNode{int data;struct AVLNode*l;struct AVLNode*r;int h;//结点的高度和深度（为了维护避免插入失衡） 
}AVLNode;//一个结点 int a[9]={1,2,3,4,5,6,7,8,9};//要插入的数据int geth(AVLNode*x)
{if(x==NULL){return 0;}else{return x->h;}
}
int maxx(int u,int v)
{if(u>v){return u;}else{return v;}
}
//调整函数：
//ll
//lr
AVLNode* LLrotation(AVLNode* x)
{AVLNode* y=x->l;x->l=y->r;//2y->r=x;//3x->h=maxx(geth(x->l),geth(x->r))+1;// 先求x的再求y的高度  y->h=maxx(geth(y->l),geth(y->r))+1;// return y;//1} 
AVLNode* RRrotation(AVLNode* x)
{AVLNode* y=x->r;x->r=y->l;//2 y->l=x;//3x->h=maxx(geth(x->l),geth(x->r))+1;y->h=maxx(geth(y->l),geth(y->r))+1;return y;//1} 
AVLNode*LRrotation(AVLNode* x)
{x->l=RRrotation(x->l);x=LLrotation(x);return x;
}AVLNode*RLrotation(AVLNode* x)
{x->r=LLrotation(x->r);x=RRrotation(x);return x;
}AVLNode* insert(AVLNode*root,int k)//插入 建立一个平衡二叉树 
{if(root==NULL)//如果根指针为空，说明还没有创建第一个结点 {AVLNode*s=(AVLNode*)malloc(sizeof(AVLNode));//创建结点 s->data=k;//赋值 s->l=s->r=NULL;//左右孩子为空 s->h=0;root=s; //根指针指向 }//说明把一个数据放在了这个结点里面了 else if(k<root->data)//如果插入的k小于根节点中的数//就让它往左孩子中插入 {root->l=insert(root->l,k);///递归写法if(geth(root->l)-geth(root->r)>1)//root失衡 ，如果让左子树插入结点后出现失衡 {if(k<root->l->data)//说明放在了左侧 ，要右旋 {//root=LLrotation(root); } else{root=LRrotation(root);//lr}} }else if(k>root->data){root->r=insert(root->r,k);if(geth(root->r)-geth(root->l)>1)//root失衡 {if(k>root->r->data){//RRroot=RRrotation(root);} else{root=RLrotation(root);//LR}} }//因为在以上插入过程中root可能进行了调整，需要重新算一下高度root->h=maxx(geth(root->l),geth(root->r))+1;return root;
}
void inorder(AVLNode*root)//遍历树 
{if(root!=NULL)//如果不为空， {inorder(root->l);//遍历左孩子因为它要保证升序序列 printf("%d ",root->data);//输出 inorder(root->r);}} 
int main()
{int i; AVLNode*root=NULL;for(i=0;i<9;i++){root=insert(root,a[i]);}inorder(root);printf("\n");printf("%d ",root->h);return 0; 
}

删除节点

AVL树的删除操作实际上是类似二叉排序树的删除操作的，无非是多了一个判断是否失衡。这里先不详细讲，有时间继续写