链式二叉树的基本操作——遍历
本文笔者将带领读者一起学习链式二叉树的一些基本语法,至于更难一些的插入删除等,笔者将在后续C++更新后再次详细带领大家学习。
首先,在进行二叉树之前,我们需要一颗二叉树,而二叉树的初始化现阶段实现不太现实,故笔者在此处手动建一个二叉树:由于现在不是堆了,所以用数组显然是不行,这时候我们直接用链表存储即可,也就是链式二叉树:
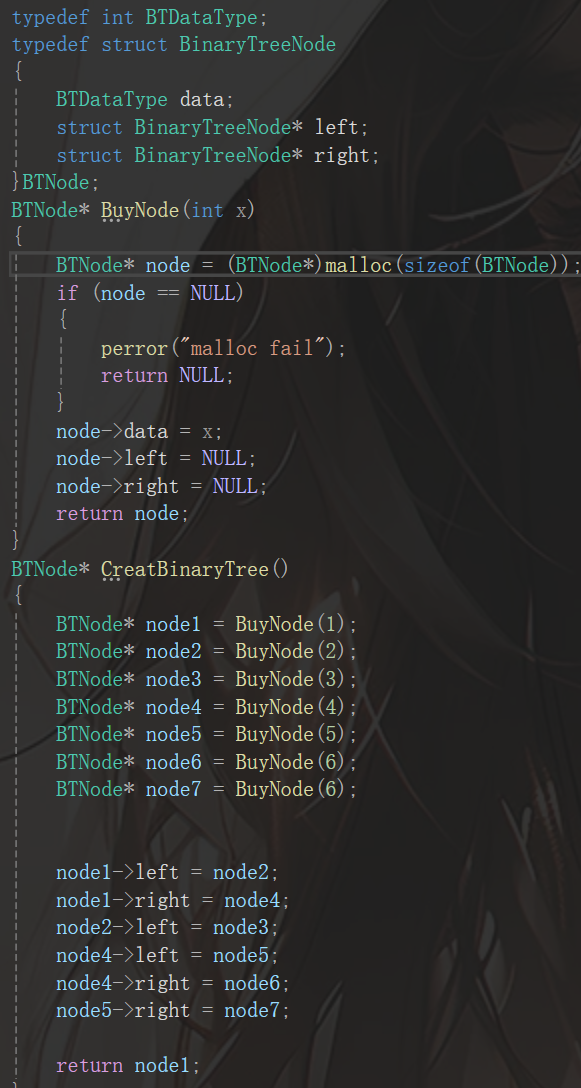
如上图,首先初始化了一个节点,然后两个指针分别指向左子树和右子树,然后手动赋值即可,最终的二叉树长这样:
1
/ \
2 4
/ / \
3 5 6
\
7
下面我们只对这个二叉树进行讨论,首先进行遍历,二叉树的遍历有三次,分别是:前序遍历,中序遍历,后序遍历。
前序遍历:根节点,左子树,右子树。由于三种遍历方式本质一样,笔者在此着重讲一下第一种遍历方式。首先,根据这棵树,我们可以借用递归的思想,不过这里有一个易错点,那就是左(右)子树是空节点时仍然存在这种情况,这里笔者记作N,一定不能忽略这种情况,比如笔者创建的这棵树,如果按照前序遍历,那就是1 (2 (3 N N) N)( 4 (5 N (7 N N))( 6 N N))不难理解,这其实是一种递归的思想,不断推进,直到遇到了N(空结点),剩下情况一直保证先根在左最后右,这是逻辑角度,下面从代码的角度来分析:

这就是一个前序遍历的代码实现,其实不难理解,这就是用了递归思想,函数栈帧的知识,因为本质上就是栈帧的调用,在具体进行时,首先需要让左子树处理完,在这之后才能进行右子树,每个二叉树都是如此进行,具体可以看下图:
 左图有些问题,不过无伤大雅,思路就是如此,最后再main函数调用一下即可:
左图有些问题,不过无伤大雅,思路就是如此,最后再main函数调用一下即可:
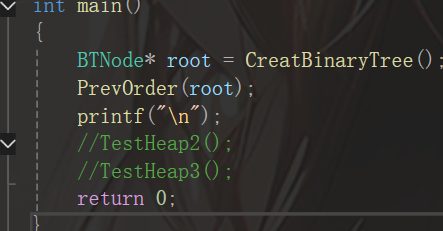
中序遍历:左子树,根节点,右子树
1
/ \
2 4
/ / \
3 5 6
\
7
中序遍历和前序遍历的情况基本一致,并无不同,中序遍历结果:((N 3 N) 2 N )1 ((N 5 (N 7 N )))4 (N 6 N))
代码自然也是类似的:
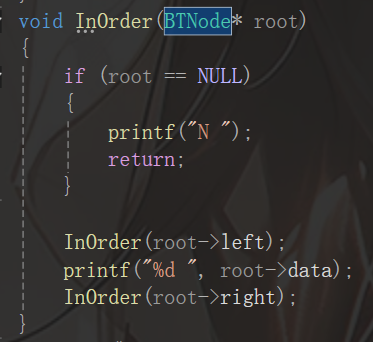
这里不作过多解释,相信读者都能理解。
后序遍历:左子树,右子树,根节点
N N 3 N 2 N N 7 N 5 N N 6 4 1
下面直接看代码:
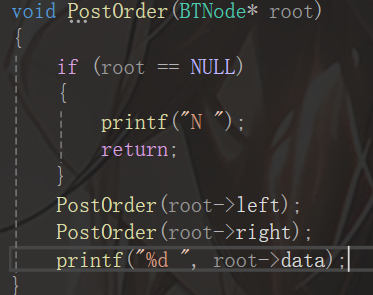
到这里,三种遍历方式其实已经结束,最后,笔者给大家看一下打印的结果:
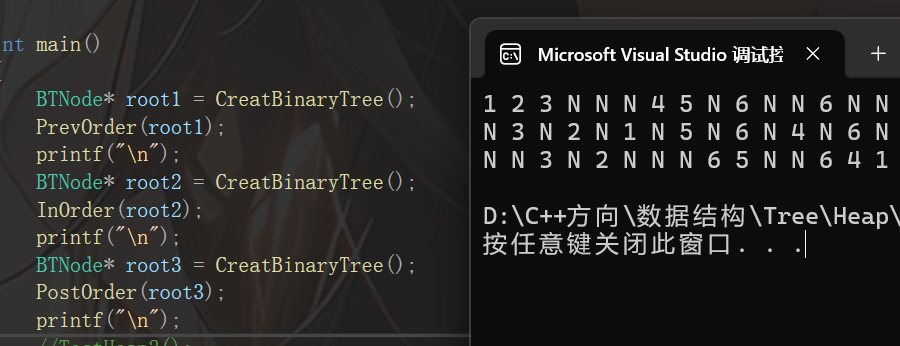
ok,到这里笔者就结束了,笔者把源码放在GitHub上了,希望大家给一个星星:
https://github.com/z-yi-han/Fundamentals-of-Data-Struct/tree/main/Tree
笔者还会持续更新,希望大家支持,非常感谢各位读者
