【CF】Day128——杂题 (图论 + 贪心 | 集合 + 贪心 + 图论 | 二分答案 + 贪心)

C. Doremy's City Construction

题目：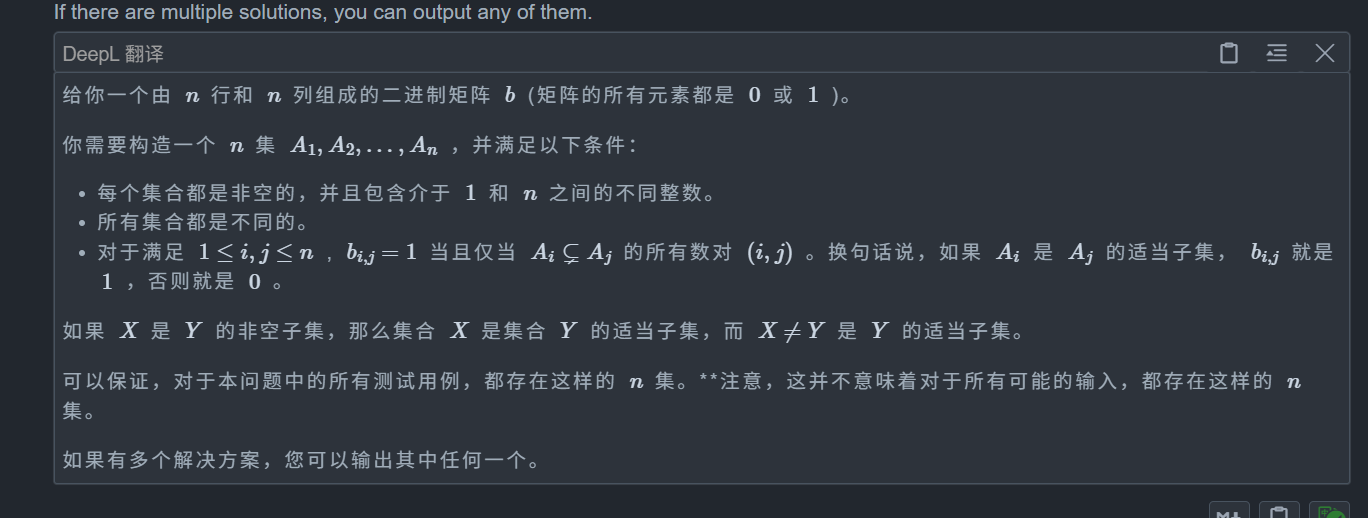

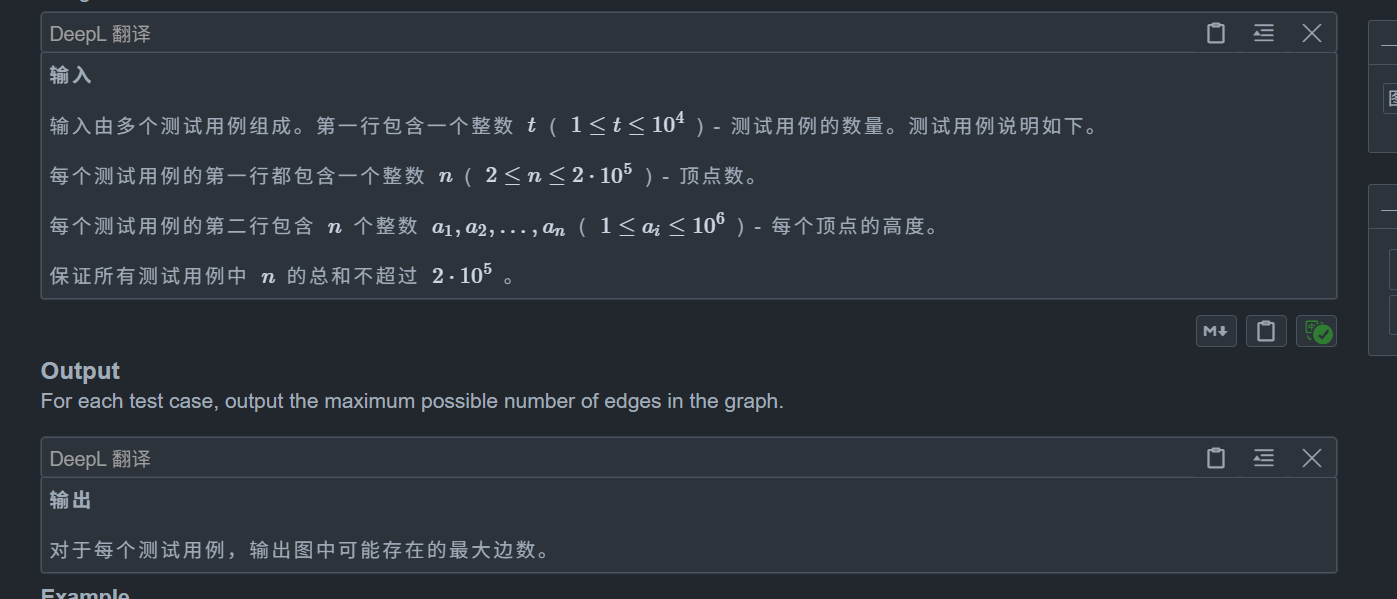思路：

trick

题目中意思缩减一下就是：如果对于一个点 i，如果我们连了比 a[i] 大的点，那么就不能连比 a[i] 小的点，同理如果连了大的就不能连小的

注意到数组顺序不影响我们连边，所以考虑先排序

对于一个数 a[i] 如果我们链接了比其大的数，那么就只能连大的数，不妨考虑将数组分成两部分，考虑前者全连后者，所以我们可以尝试暴力枚举 a[i]，然后二分出第一个大于 a[i] 的位置 pos，那么此时的奉献根据乘法原理可得 ans = pos * (n - pos)，全程枚举存储最大值即可

特别注意我们有一个特殊情况，我们如果只有 a[i]，那么就只能两两连一条边，即 n / 2

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n;cin >> n;vector<int> a(n);int allsame = 1;for (int i = 0; i < n; i++){cin >> a[i];if(a[i] != a[0]) allsame = 0;}if(allsame){cout << n/2 << endl;return;}sort(a.begin(),a.end());int ans = 0;for (int i = 0; i < n; i++){auto pos = upper_bound(a.begin(),a.end(),a[i]) - a.begin();ans = max(ans,pos * (n - pos));}cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

C. Set Construction

题目：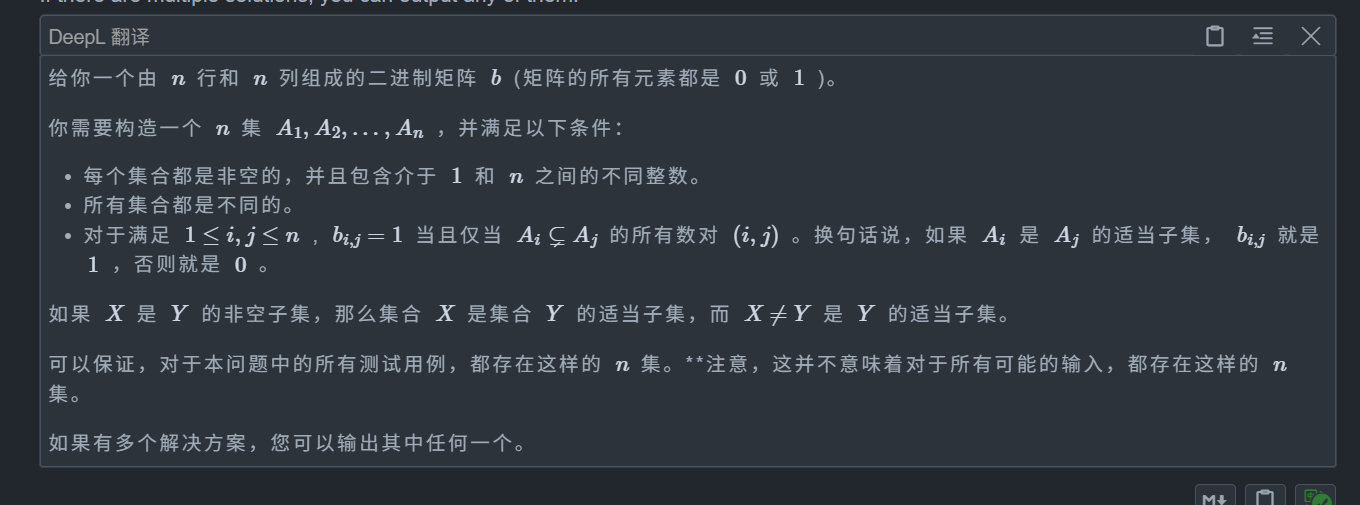

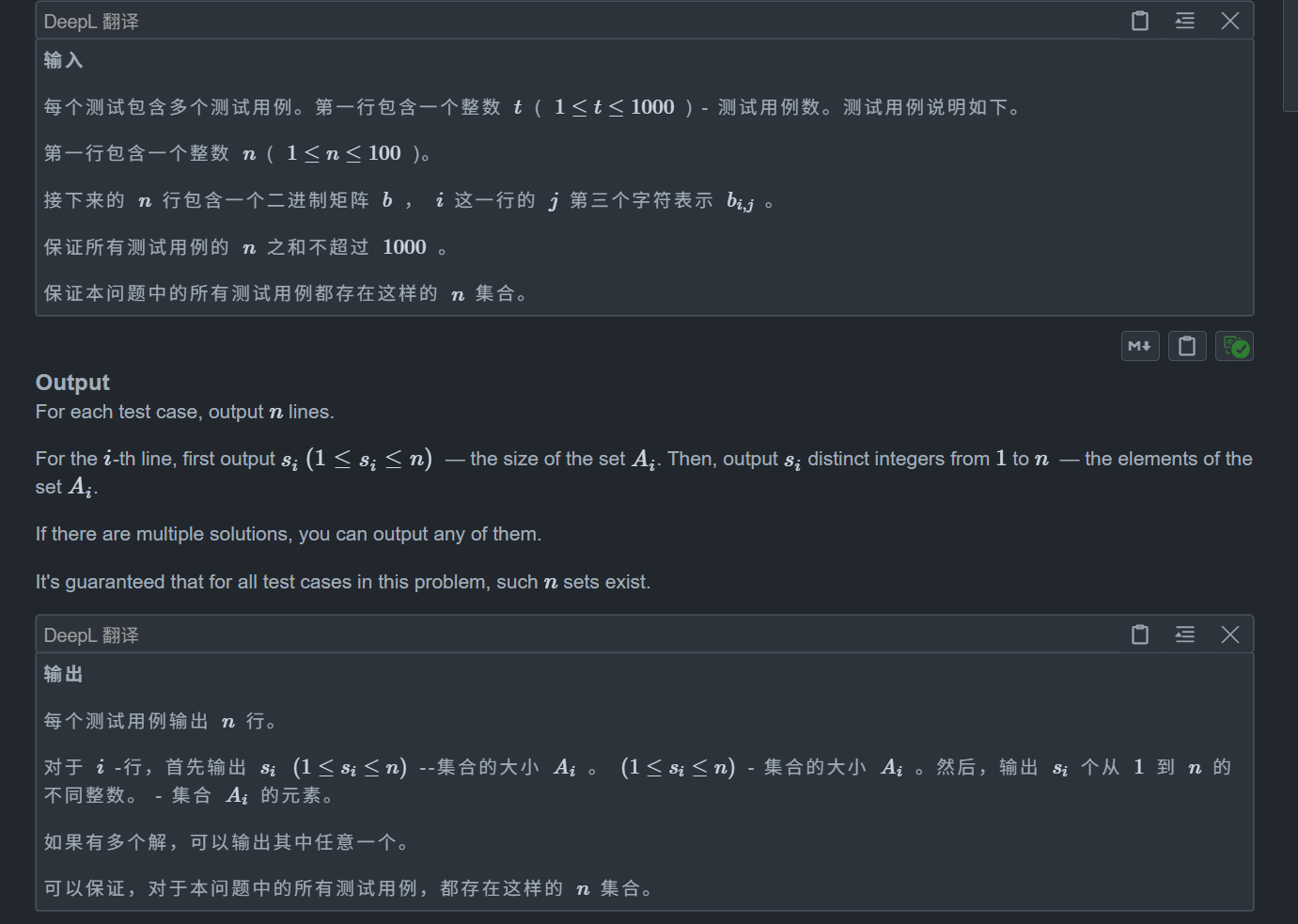思路：

很巧妙的一题

这题可以看作图来写，但是一开始没想到如何分配初始值比较好

我们不妨将关系图看成一个图，那么对于 (i,j) 如果是 1，那么说明 i->j 有一条有向边，那么进一步思考就是 i 的所有值都属于 j，且 j 的值比 i 还多

那我们不妨考虑分配1~n的值给每一个点，这样每个集合肯定不会重复，然后根据其关系图我们传递值即可，具体的我们只传递初始值，这样就能保证子集的同时不会重复了

为什么只用传递初始值呢？显然如果 i 是 j 的子集，而 j 又是 z 的子集，那么关系图上肯定会显示 i->z的边，题目保证一定有解，所以这是可行的

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n;cin >> n;vector<string> mp(n);vector<vector<int>> ans(n);for (int i = 0; i < n; i++){ans[i].push_back(i + 1);}for (int i = 0; i < n; i++){cin >> mp[i];for (int j = 0; j < mp[i].size(); j++){if (mp[i][j] == '1'){ans[j].push_back(ans[i].front());}}}for (int i = 0; i < n; i++){cout << ans[i].size() << " ";for (auto &x : ans[i]){cout << x << " ";}cout << endl;}
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

F. Quests

题目：

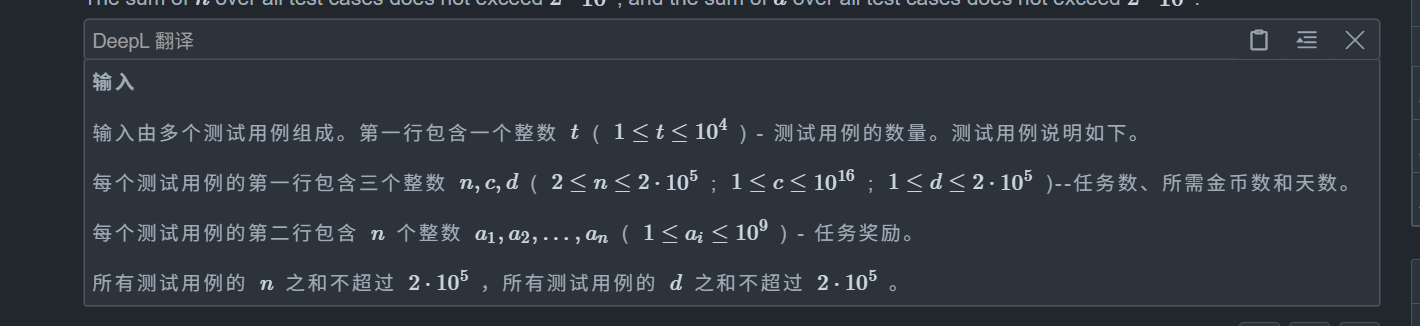
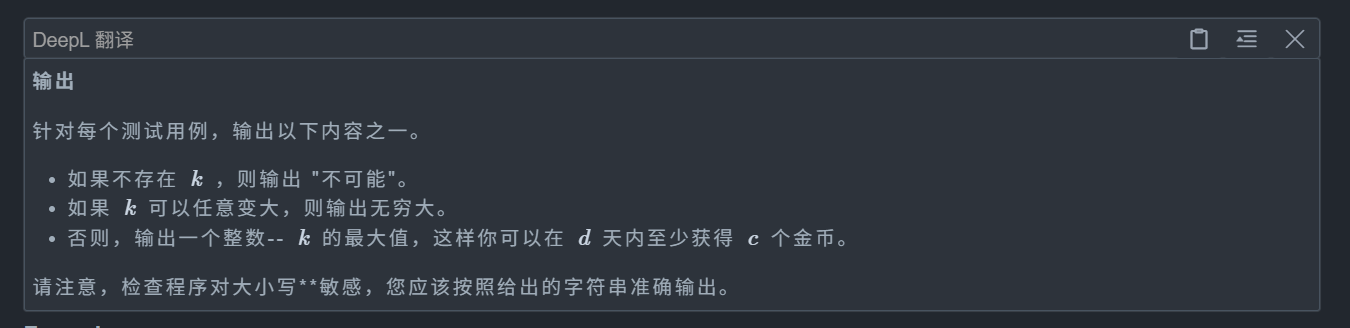思路：

有点细节的二分

不难看出本题具有二分性，如果 x 可以，那么 0 ~ x-1 肯定也可以，所以我们考虑二分答案

我们发现我们可以任意安排任务的执行顺序，那么显然我们肯定是贪心的选取，即先选大的再选小的，所以考虑将数组降序排列，同时为了快速得知一段区间的和，我们还得初始化一下前缀和，方便后续 check

随后我们尝试 check，我们注意到如果我们选的天数是 k，那么其实是以 k + 1 为一个周期的，观察样例也可以发现，所以我们计算时需要注意了

对于 check 部分，我们先看看能进行多少个周期，即先选  sum[min(n, k + 1)] * (d / (k + 1))，为什么是 min(n, k + 1) 呢？因为我们是以 k + 1 为一个周期，同时如果 k + 1 >= n，那么我们多出的地方也选不了了，即空的，所以最大只能是 n，否则我们肯定是将空处也选上

然后由于我们可能无法整除，所以最后还要看看余数还能选多少，具体看代码即可

特别的，对于无限的情况，此时 k >= d，否则如果都不行则无解

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n, c, d;cin >> n >> c >> d;vector<int> task(n + 1);for (int i = 1; i <= n; i++){cin >> task[i];}sort(task.begin() + 1, task.end(), greater<>());vector<int> sum(n + 2, 0);for (int i = 1; i <= n; i++){sum[i] = sum[i - 1] + task[i];}sum[n + 1] = sum[n];auto check = [&](int k) -> int{//周期是 k+1，那么看看有多少个周期可以取int tot = sum[min(n, k + 1)] * (d / (k + 1));//然后看看剩下天数能取多少tot += sum[min(n, d % (k + 1))];return tot >= c;// int len = min(k, n) + 1;// int T = c / sum[len];// if(c % sum[len] == 0)// {//     T--;// }// int costday = T * k + T;// int last = c - T * sum[len];// for (int i = 0; i <= n; i++)// {//     if (sum[i] >= last)//     {//         costday += i;//         break;//     }// }// return costday <= d;};int l = 0, r = 1e12;while (l + 1 < r){int mid = l + r >> 1;if (check(mid)){l = mid;}else{r = mid;}}if (check(r)){if (r >= d){cout << "Infinity\n";}else{cout << r << endl;}}else if (check(l)){if (l >= d){cout << "Infinity\n";}else{cout << l << endl;}}else{cout << "Impossible\n";}
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}