机器学习项目从零到一：加州房价预测模型（PART 3）

一、食用指南

本系列文章将实现一个端到端的机器学习项目案例。假设你是一个A公司最近新雇用的数据科学家，以下是你将会经历的主要步骤：

1. 观察大局。
2. 获得数据。
3. 从数据探索和可视化中获得洞见。
4. 机器学习算法的数据准备。
5. 选择并训练模型。
6. 微调模型。
7. 展示解决方案。
8. 启动、监控和维护系统。

项目案例纯属虚构，目的仅仅是为了说明机器学习项目的主要步骤。

二、选择和训练模型

书接上文：

机器学习项目从零到一：加州房价预测模型（PART 1）

机器学习项目从零到一：加州房价预测模型（PART 2）

我们提出了问题，获得了数据，也进行了数据探索，然后对训练集和测试集进行了抽样并编写了转换流水线，从而可以自动清理和准备机器学习算法的数据！现在是时候选择机器学习模型并展开训练了。

1、线性回归模型

使用 LinearRegression 训练一个线性回归模型是一个相对简单的过程，它需要两组数据：

• ​特征（X）​：通常是自变量，形状为 (样本数, 特征数)，比如 (100, 3) 表示 100 个样本，每个样本有 3 个特征。
• ​目标（y）​：通常是因变量（要预测的值），形状为 (样本数,) 或 (样本数, 1)。

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.metrics import mean_squared_error, r2_score# 1. 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 3. 创建并训练模型
model = LinearRegression()
model.fit(X_train, y_train)# 4. 查看模型参数
print("截距 (Intercept):", model.intercept_)
print("系数 (Coefficients):", model.coef_)# 5. 进行预测
y_pred = model.predict(X_test)# 6. 评估模型
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_pred)print("均方误差 (MSE):", mse)
print("均方根误差 (RMSE):", rmse)
print("R² 分数:", r2)

截距 (Intercept): [4.14291332]
系数 (Coefficients): [[2.79932366]]
均方误差 (MSE): 0.6536995137170021
均方根误差 (RMSE): 0.8085168605026132
R² 分数: 0.8072059636181392

2、训练与评估模型

线性回归模型

使用训练集训练一个线性回归模型：

from sklearn.linear_model import LinearRegressionlin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)

现在我们有一个可以工作的线性回归模型了，可以用几个训练集的实例试试效果：

# let's try the full preprocessing pipeline on a few training instances
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)print("Predictions:", lin_reg.predict(some_data_prepared))

Predictions: [378700.86021795 413552.59083358 222954.90136548  90023.58156553167575.50734299]

虽然预测还不是很准确，但至少能跑通了。我们可以使用 Scikit-Learn 的 mean_squared_error函数来测量整个训练集上回归模型的RMSE：

from sklearn.metrics import mean_squared_errorhousing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse

68367.49588146957

大多数区域的 median_housing_values 分布在 120000～265000 美元之间，所以典型的预测误差达到 68628 美元属于是糟糕的结果，这就是一个典型的模型对训练数据欠拟合的案例。这种情况发生时，通常意味着这些特征可能无法提供足够的信息来做出更好的预测，或者是模型本身不够强大。想要修正欠拟合，可以通过选择更强大的模型，或为算法训练提供更好的特征，又或者减少对模型的限制等方法。

决策树模型

我们尝试训练一个 DecisionTreeRegressor，这是一个非常强大的模型，它能够从数据中找到复杂的非线性关系：

from sklearn.tree import DecisionTreeRegressortree_reg = DecisionTreeRegressor(random_state=42)
tree_reg.fit(housing_prepared, housing_labels)

测试模型效果：

housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse

等等，什么！完全没有错误？这个模型真的可以做到绝对完美吗？当然，更有可能的是这个模型对数据严重过拟合了。为了验证模型效果，我们需要拿训练集中的一部分用于训练，另一部分用于模型验证。

评估决策树模型的一种方法是使用 train_test_split 函数将训练集分为较小的训练集和验证集，然后根据这些较小的训练集来训练模型，并对其进行评估。这虽然有一些工作量，但是不会太难，并且非常有效。

另一个不错的选择是使用 Scikit-Learn 的 K-折交叉验证功能。以下是执行K-折交叉验证的代码：

from sklearn.model_selection import cross_val_scorescores = cross_val_score(tree_reg, housing_prepared, housing_labels,scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-scores)

它将训练集随机分割成10个不同的子集，每个子集称为一个折叠，然后对决策树模型进行10次训练和评估（每次挑选1个折叠进行评估，使用另外的9个折叠进行训练），产生的结果是一个包含10次评估分数的数组。让我们看看结果：

def display_scores(scores):print("Scores:", scores)print("Mean:", scores.mean())print("Standard deviation:", scores.std())display_scores(tree_rmse_scores)

Scores: [67161.394198   68253.43012633 67403.31669457 66901.9241351170769.59498776 73849.23673435 66203.93613635 72253.2803447368055.5001325  69559.81918889]
Mean: 69041.14326785851
Standard deviation: 2390.1062127163027

这次的决策树模型好像不如之前表现得好。事实上，它看起来简直比线性回归模型还要糟糕！保险起见，让我们也计算一下线性回归模型的评分：

lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)

Scores: [67016.77486879 69544.1051662  66608.55215828 67913.8055206471005.71791236 69406.29286953 67770.84270401 68180.8695876571088.90442213 68411.97282271]
Mean: 68694.78380322951
Standard deviation: 1458.6151818900632

没错，决策树模型确实是严重过拟合了，以至于表现得比线性回归模型还要糟糕。

\	第一组数据 tree_rmse_scores	第二组数据 lin_rmse_scores
均值 Mean	69041.143	68694.784
标准差 Standard deviation	2390.106	1458.615
解释	模型预测误差较大，且不同折之间的性能波动显著（标准差高），表明模型可能过拟合或数据存在高方差问题。	均值更低（预测误差更小），标准差显著更小，说明模型性能更稳定，泛化能力更强。

随机森林模型

我们再来试试最后一个模型：RandomForestRegressor 。

# 训练
from sklearn.ensemble import RandomForestRegressorforest_reg = RandomForestRegressor(n_estimators=100, random_state=12)
forest_reg.fit(housing_prepared, housing_labels)

# 预测
housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse

18463.129393231982

# 验证
from sklearn.model_selection import cross_val_scoreforest_scores = cross_val_score(forest_reg, housing_prepared, housing_labels,scoring="neg_mean_squared_error", cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)

Scores: [47888.30145319 50444.26833518 48200.99204427 50307.8719123951231.73955638 50175.0145104  47758.21352096 50029.3617982249812.10474945 49655.52519804]
Mean: 49550.33930784934
Standard deviation: 1126.6836790131595

哇，这个就好多了，随机森林模型看起来很有戏。

\	第一组数据 tree_rmse_scores	第二组数据 lin_rmse_scores	第三组数据 lin_rmse_scores
均值 Mean	69041.143	68694.784	49550.339
标准差 Standard deviation	2390.106	1458.615	1126.683
解释	模型预测误差较大，且不同折之间的性能波动显著（标准差高），表明模型可能过拟合或数据存在高方差问题。	均值更低（预测误差更小），标准差显著更小，说明模型性能更稳定，泛化能力更强。	均值显著更低（预测误差更小），标准差更小，说明模型性能更稳定，泛化能力更强。

但是注意到训练集上的分数为 18463.129，与 49550.339 相比要低得多，训练效果与验证效果相差太大，这意味着模型仍然存在相当多的过拟合。

其他模型

我们需要尝试一遍各种机器学习算法的其他模型（几种具有不同内核的支持向量机，比如神经网络模型等），但是记住，别花太多时间去调整超参数，我们的目的是筛选出几个（2～5个）有效的模型。

3、保存模型

每一个尝试过的模型都应该妥善保存，以便将来可以轻松回到我们想要的模型当中。记得还要同时保存超参数和训练过的参数，以及交叉验证的评分和实际预测的结果，这样就可以轻松地对比不同模型类型的评分，以及不同模型造成的错误类型。通过Python的pickle模块或joblib库，我们可以轻松保存Scikit-Learn模型，这样可以更有效地将大型NumPy数组序列化。

import joblib
joblib.dump(forest_reg, "my_model.pkl")
# and later...
my_model_loaded = joblib.load("my_model.pkl")

三、微调模型

我们来看几个可行的模型微调方法。

1、网格搜索

一种微调的方法是手动调整超参数，直到找到一组很好的超参数值组合，这个过程非常麻烦且耗时。因此，我们可以用Scikit-Learn的GridSearchCV来进行探索，要做的只是告诉它要进行实验的超参数是什么，以及需要尝试的值，它将会使用交叉验证来评估超参数值的所有可能组合。

from sklearn.model_selection import GridSearchCVparam_grid = [# try 12 (3×4) combinations of hyperparameters{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},# then try 6 (2×3) combinations with bootstrap set as False{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},]forest_reg = RandomForestRegressor(random_state=42)
# train across 5 folds, that's a total of (12+6)*5=90 rounds of training 
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,scoring='neg_mean_squared_error',return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)

例如，上面这段代码搜索 RandomForestRegressor 的超参数值的最佳组合。

！当你不知道超参数应该赋什么值时，一个简单的方法是尝试10的连续幂次方（如果你想要得到更细粒度的搜索，可以使用更小的数，参考这个示例中所示的n_estimators超参数）

这个param_grid告诉Scikit-Learn，首先评估第一个dict中的n_estimator和max_features的所有3×4=12种超参数值组合；接着，尝试第二个dict中超参数值的所有2×3=6种组合，但这次超参数bootstrap需要设置为False而不是True（True是该超参数的默认值）。

总而言之，网格搜索将探索RandomForestRegressor超参数值的12+6=18种组合，并对每个模型进行5次训练（因为我们使用的是5-折交叉验证），所以总共会完成18×5=90次训练！这可能需要相当长的时间，但是完成后我们就可以获得最佳的参数组合：

grid_search.best_params_

{'max_features': 8, 'n_estimators': 30}

因为被评估的n_estimator最大值是8和30，所以我们还可以调整代码中的上限值，评分可能还会继续改善。

我们可以直接得到最好的估算器：

grid_search.best_estimator_

如果GridSearchCV被初始化为refit=True（默认值），那么一旦通过交叉验证找到了最佳估算器，它将在整个训练集上重新训练。这通常是个好方法，因为提供更多的数据很可能提升其性能。

当然还有评估分数：

cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):print(np.sqrt(-mean_score), params)

64522.72482201707 {'max_features': 2, 'n_estimators': 3}
55529.27068244215 {'max_features': 2, 'n_estimators': 10}
52890.199903489076 {'max_features': 2, 'n_estimators': 30}
59734.585551784265 {'max_features': 4, 'n_estimators': 3}
52228.36219034505 {'max_features': 4, 'n_estimators': 10}
50157.81868504187 {'max_features': 4, 'n_estimators': 30}
57242.93415896869 {'max_features': 6, 'n_estimators': 3}
51217.96054126871 {'max_features': 6, 'n_estimators': 10}
49759.66910226915 {'max_features': 6, 'n_estimators': 30}
57698.90619569072 {'max_features': 8, 'n_estimators': 3}
51744.17895082832 {'max_features': 8, 'n_estimators': 10}
49612.20736359233 {'max_features': 8, 'n_estimators': 30}
61711.17181120399 {'bootstrap': False, 'max_features': 2, 'n_estimators': 3}
54197.150065271104 {'bootstrap': False, 'max_features': 2, 'n_estimators': 10}
59411.46437964344 {'bootstrap': False, 'max_features': 3, 'n_estimators': 3}
52550.51890890605 {'bootstrap': False, 'max_features': 3, 'n_estimators': 10}
58784.12365316802 {'bootstrap': False, 'max_features': 4, 'n_estimators': 3}
51157.546078470084 {'bootstrap': False, 'max_features': 4, 'n_estimators': 10}

在本例中，我们得到的最佳解决方案是将超参数max_features设置为8，将超参数n_estimators设置为30，这个组合的RMSE分数为49612.207，与之前使用默认超参数值的分数 49550.339 非常接近。

至此，我们已经将模型调整到了最佳模式！

2、随机搜索

如果探索的组合数量较少（例如上一个示例），那么网格搜索是一种不错的方法。但是当超参数的搜索范围较大时，通常会优先选择使用RandomizedSearchCV，这个类用起来与GridSearchCV类大致相同，但它不会尝试所有可能的组合，而是在每次迭代中为每个超参数选择一个随机值，然后对一定数量的随机组合进行评估。

这种方法有两个显著好处：

• 如果运行随机搜索1000个迭代，那么将会探索每个超参数的1000个不同的值（而不是像网格搜索方法那样每个超参数仅探索少量几个值）。
• 通过简单地设置迭代次数，可以更好地控制要分配给超参数搜索的计算预算。

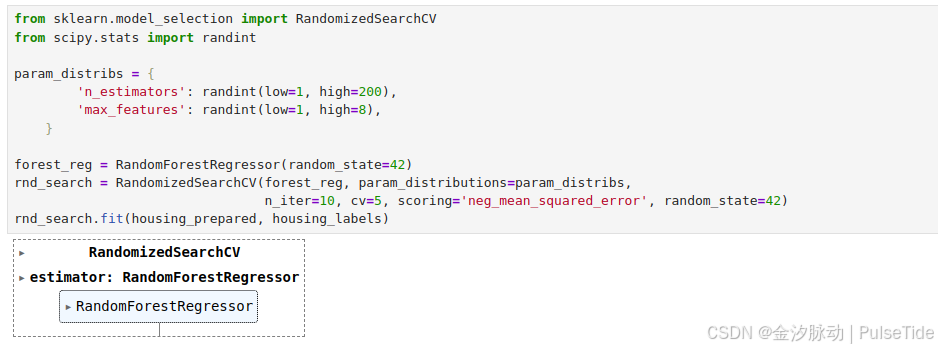
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randintparam_distribs = {'n_estimators': randint(low=1, high=200),'max_features': randint(low=1, high=8),}forest_reg = RandomForestRegressor(random_state=42)
rnd_search = RandomizedSearchCV(forest_reg, param_distributions=param_distribs,n_iter=10, cv=5, scoring='neg_mean_squared_error', random_state=42)
rnd_search.fit(housing_prepared, housing_labels)

cvres = rnd_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):print(np.sqrt(-mean_score), params)

48776.603209827066 {'max_features': 7, 'n_estimators': 180}
51343.085415311805 {'max_features': 5, 'n_estimators': 15}
50324.49362757991 {'max_features': 3, 'n_estimators': 72}
50584.00330264014 {'max_features': 5, 'n_estimators': 21}
48958.45084980925 {'max_features': 7, 'n_estimators': 122}
50313.49592247687 {'max_features': 3, 'n_estimators': 75}
50175.25896891767 {'max_features': 3, 'n_estimators': 88}
49262.164103040916 {'max_features': 5, 'n_estimators': 100}
50041.68738628071 {'max_features': 3, 'n_estimators': 150}
65158.58452404853 {'max_features': 5, 'n_estimators': 2}

3、集成方法

还有一种微调系统的方法是将表现最优的模型组合起来。组合（或“集成”）方法通常比最佳的单一模型更好（就像随机森林比其所依赖的任何单个决策树模型更好一样），特别是当单一模型会产生不同类型误差时更是如此。

4、分析最佳模型及其误差

通过检查最佳模型，我们总是可以得到一些好的洞见。例如在进行准确预测时，RandomForestRegressor可以指出每个属性的相对重要程度：

feature_importances = grid_search.best_estimator_.feature_importances_
feature_importances

array([7.17141522e-02, 6.36243614e-02, 4.08336725e-02, 1.43179499e-02,1.43814607e-02, 1.46824354e-02, 1.32477467e-02, 3.83137424e-01,5.67390749e-02, 1.06525449e-01, 4.98279635e-02, 7.53878528e-03,1.58097793e-01, 1.88530133e-04, 1.87980426e-03, 3.26339789e-03])

将这些重要性分数显示在对应的属性名称旁边：

extra_attribs = ["rooms_per_hhold", "pop_per_hhold", "bedrooms_per_room"]
#cat_encoder = cat_pipeline.named_steps["cat_encoder"] # old solution
cat_encoder = full_pipeline.named_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)

[(0.3831374235182108, 'median_income'),(0.15809779292028256, 'INLAND'),(0.10652544884603964, 'pop_per_hhold'),(0.07171415216776203, 'longitude'),(0.06362436135294293, 'latitude'),(0.05673907494418143, 'rooms_per_hhold'),(0.04982796351625397, 'bedrooms_per_room'),(0.0408336724678324, 'housing_median_age'),(0.014682435358600684, 'population'),(0.014381460708722428, 'total_bedrooms'),(0.014317949944562761, 'total_rooms'),(0.013247746685900261, 'households'),(0.0075387852831522925, '<1H OCEAN'),(0.0032633978895144217, 'NEAR OCEAN'),(0.0018798042630391323, 'NEAR BAY'),(0.00018853013300234098, 'ISLAND')]

有了这些信息，我们可以尝试删除一些不太有用的特征（这里不做展开，只作为切入点）。

5、通过测试集评估模型

现在是用测试集评估最终模型的时候了，这个过程没有什么特别的，只需要从测试集中获取预测器和标签，运行full_pipeline来转换数据（调用transform而不是fit_transform），然后在测试集上评估最终模型：

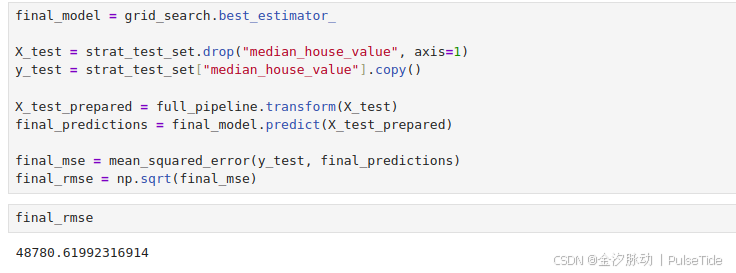
final_model = grid_search.best_estimator_X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)

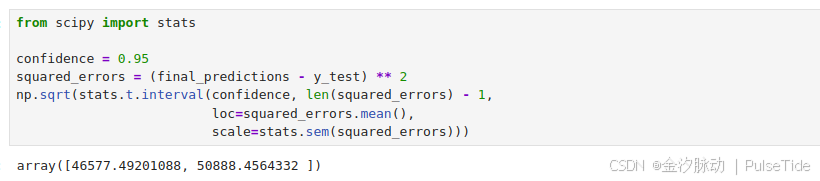
在某些情况下，泛化误差的这种点估计的说服力不强：假如它仅比当前生产环境中的模型好0.1%？我们需要知道这个估计的精确度，为此，我们可以使用scipy.stats.t.interval计算泛化误差的95%置信区间：

from scipy import statsconfidence = 0.95
squared_errors = (final_predictions - y_test) ** 2
np.sqrt(stats.t.interval(confidence, len(squared_errors) - 1,loc=squared_errors.mean(),scale=stats.sem(squared_errors)))

如果之前进行过大量的超参数调整，这时的评估结果通常会略逊于我们之前使用交叉验证时的表现结果（因为通过不断调整，系统在验证数据上终于表现良好，在未知数据集上可能达不到这么好的效果）。在本例中，结果虽然并非如此，但是当这种情况发生时，我们一定不要继续调整超参数，不要试图再努力让测试集的结果变得好看一些，因为这些改进在泛化到新的数据集时又会变成无用功。

四、展示解决方案

现在进入项目预启动阶段：我们将要展示解决方案（强调学习了什么，什么有用，什么没有用，基于什么假设，以及系统的限制有哪些），记录所有事情，通过清晰的可视化和易于记忆的陈述方式制作漂亮的演示文稿（例如，“收入中位数是预测房价的首要指标”）。在这个加州住房的示例里，系统的最终性能并不比专家估算的效果好，通常会下降20%左右，但这仍然是一个不错的选择，因为这为专家腾出了一些时间以便他们可以投入更有趣和更有生产力的任务上。

五、启动、监控和维护系统

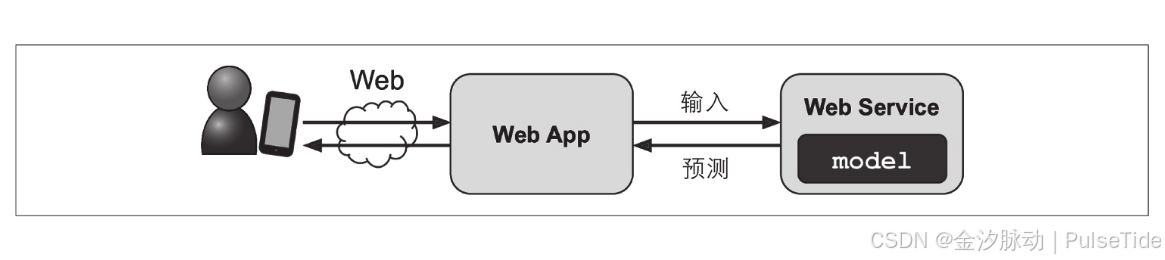
很好，我们已获准启动生产环境！现在，我们需要准备好解决方案以进行上线（例如，完善代码、编写文档和测试等），然后将模型部署到生产环境中。

一种方法是保存训练好的Scikit-Learn模型（使用joblib），包括完整的预处理和预测流水线，然后在生产环境中加载经过训练的模型并通过调用prepare方法来进行预测。例如，也许该模型在网站内使用：用户将输入有关新地区的一些数据，然后单击估算价格按钮,这将发送一个查询，其中包含数据发送到Web服务器，然后将其转发到Web应用程序，最后，我们的代码调用模型的predict方法（在服务器启动时加载模型，而不是每次使用模型时都加载模型）。

或者，我们可以将模型包装在Web应用程序中，使用专用的Web服务，通过REST API来进行查询。这样可以轻松地将模型升级到新版本，而不会中断主应用程序。这样也简化了扩展，因为可以根据需要来启动任意数量的Web服务，并且平衡那些Web服务上Web应用程序的请求负载，而且，它允许你的Web应用程序使用任何语言，而不仅仅是Python。

但是部署并不是故事的结束。我们还需要编写监控代码以定期检查系统的实时性能，并在系统性能降低时触发警报。由于基础架构中的组件损坏，性能下降可能会很大，但也有可能是轻微的下降，长时间内很容易被忽视，这很常见，因为模型会随着时间的流逝而失效：的确，世界在变化，因此，如果使用去年的数据对模型进行训练，则可能不会适应今天的数据。

因此，我们需要监控模型的实时性能。但是怎么做呢？在某些情况下，可以从下游推断模型的性能指标。例如，如果我们的模型是推荐系统的一部分，并且推荐用户可能感兴趣的产品，那么很容易监控每天已出售的推荐产品的数量。如果该数字下降（与不推荐相比），那么主要的嫌疑就是模型，这可能是因为数据流水线断开，或者可能需要对新数据重新训练模型。

但是，有些情况我们需要人工分析才能知道模型的性能是否下降。例如，假设我们训练了一个图像分类模型来检测生产线上的产品缺陷。怎么才能在数以千计的次品发货给客户之前，得到模型的性能是否下降的警告？一种解决方案是将一些模型分类的图片（尤其是对模型来说不确定的图片）送给人工评估者。根据任务，评估者可能需要是专家或者非专家，例如众包平台上的工人。在某些应用中，他们甚至可能是用户自己。

无论哪种方式，我们都需要建立一个监控系统（是否有人来评估实时模型），以及所有的相关流程，以定义发生故障怎么做以及如何为故障做准备。是的，这可能需要做很多工作，实际上，工作量通常比构建和训练模型要多得多。