VMD例程(Matlab 2021b可直接使用)
VMD已是该领域大家熟知的算法了,各种教程与解析已经铺天盖地了,本文仅给出算法供大家调用验证,不进行解析。
function [u, u_hat, omega] = VMD(signal, fs, alpha, tau, K, DC, init, tol)
% Variational Mode Decomposition (Modified Version)
% Authors: Konstantin Dragomiretskiy and Dominique Zosso
% Modified by: [Your Name/Organization], [Date]
%
% Input Parameters:
% -----------------
% signal - 输入信号 (1D 时域信号)
% fs - 采样频率 (Hz) [添加实际采样频率]
% alpha - 数据保真度约束的平衡参数
% tau - 对偶上升的时间步长 (噪声容限,取0表示无松弛)
% K - 要恢复的模态数量
% DC - 是否将第一模态设为直流分量 (true/false)
% init - 中心频率初始化方式:
% 0 = 全部从0开始
% 1 = 均匀分布初始化
% 2 = 随机初始化
% tol - 收敛容差 (推荐 1e-6)
%
% Output:
% -------
% u - 分解后的模态集合 (K x 信号长度)
% u_hat - 模态的频谱 (信号长度 x K)
% omega - 估计的模态中心频率 (Hz) [输出实际频率]
%
% 参考文献:
% K. Dragomiretskiy, D. Zosso, Variational Mode Decomposition,
% IEEE Trans. on Signal Processing, 62(3):531-544, 2014
% DOI: 10.1109/TSP.2013.2288675% ---------- 准备工作 ----------
save_T = length(signal); % 原始信号长度
T = save_T; % 当前信号长度% 通过镜像延拓处理边界效应
f_mirror(1:T/2) = signal(T/2:-1:1);
f_mirror(T/2+1:3*T/2) = signal;
f_mirror(3*T/2+1:2*T) = signal(T:-1:T/2+1);
f = f_mirror;% 延拓后的时间域 (0 到 T)
T = length(f);
t = (1:T)/T;% 频谱域离散化 (归一化频率 -0.5 到 0.5)
freqs_norm = t - 0.5 - 1/T;% 最大迭代次数
N = 500;% 为每个模态设置alpha参数
Alpha = alpha * ones(1, K);% FFT计算及中心化处理
f_hat = fftshift(fft(f));
f_hat_plus = f_hat;
f_hat_plus(1:T/2) = 0; % 仅保留正频率部分% 预分配存储空间 (优化:只存储当前和上一次迭代)
u_hat_plus = zeros(2, length(freqs_norm), K); % 改为循环缓冲区
lambda_hat = zeros(2, length(freqs_norm)); % 对偶变量存储% 中心频率初始化
omega_plus = zeros(2, K); % [当前, 上一次]
switch initcase 1 % 均匀分布for i = 1:Komega_plus(1, i) = (0.5/K) * (i-1);endcase 2 % 随机初始化 (使用实际频率范围)omega_plus(1, :) = sort(rand(1, K) * (fs/2)); % 使用实际频率otherwise % 全零初始化omega_plus(1, :) = 0;
end% 如果要求DC模式,强制第一个中心频率为0
if DComega_plus(1, 1) = 0;
end% 迭代控制变量
uDiff = tol + eps; % 更新步长
n = 1; % 迭代计数器
sum_uk = 0; % 累加器% ---------- 主迭代循环 ----------
while (uDiff > tol && n < N)% 使用循环缓冲区索引 (1=当前, 2=上一次)curr = mod(n-1, 2) + 1;next = mod(n, 2) + 1;% 更新第一个模态k = 1;sum_uk = u_hat_plus(curr, :, K) + sum_uk - u_hat_plus(curr, :, 1);% 通过维纳滤波器更新模态频谱u_hat_plus(next, :, k) = (f_hat_plus - sum_uk - lambda_hat(curr, :)/2) ./ ...(1 + Alpha(k) * (freqs_norm - omega_plus(curr, k)).^2);% 更新中心频率 (非DC模式)if ~DCidx = (T/2+1):T; % 正频率索引spec = abs(u_hat_plus(next, idx, k)).^2;omega_plus(next, k) = sum(freqs_norm(idx) .* spec) / sum(spec);elseomega_plus(next, k) = omega_plus(curr, k);end% 更新其他模态for k = 2:Ksum_uk = u_hat_plus(next, :, k-1) + sum_uk - u_hat_plus(curr, :, k);% 模态频谱更新u_hat_plus(next, :, k) = (f_hat_plus - sum_uk - lambda_hat(curr, :)/2) ./ ...(1 + Alpha(k) * (freqs_norm - omega_plus(curr, k)).^2);% 中心频率更新idx = (T/2+1):T;spec = abs(u_hat_plus(next, idx, k)).^2;omega_plus(next, k) = sum(freqs_norm(idx) .* spec) / sum(spec);end% 对偶上升 (更新拉格朗日乘子)lambda_hat(next, :) = lambda_hat(curr, :) + ...tau * (sum(u_hat_plus(next, :, :), 3) - f_hat_plus);% 计算收敛条件uDiff = 0;for k = 1:Kdiff_spec = u_hat_plus(next, :, k) - u_hat_plus(curr, :, k);uDiff = uDiff + (1/T) * (diff_spec * diff_spec');enduDiff = abs(uDiff);% 迭代计数器更新n = n + 1;
end% ---------- 后处理 ----------
% 最终迭代索引
final_idx = mod(n-1, 2) + 1;% 信号重构
u_hat = zeros(T, K);
u_hat((T/2+1):T, :) = squeeze(u_hat_plus(final_idx, (T/2+1):T, :));
u_hat((T/2+1):-1:2, :) = conj(squeeze(u_hat_plus(final_idx, (T/2+1):T, :)));
u_hat(1, :) = conj(u_hat(end, :));% 时域模态重建
u = zeros(K, T);
for k = 1:Ku(k, :) = real(ifft(ifftshift(u_hat(:, k).')));
end% 移除镜像部分
u = u(:, T/4+1:3*T/4);% 重新计算实际长度信号的频谱
u_hat = zeros(save_T, K);
for k = 1:Ku_hat(:, k) = fftshift(fft(u(k, :))).';
end% 转换中心频率到实际频率 (Hz) [关键修复]
omega = omega_plus(final_idx, :) * fs;end测试:
% 生成测试信号
fs = 1000; % 采样频率 1000 Hz
t = 0:1/fs:1-1/fs; % 1秒时长
f1 = 50; % 50Hz分量
f2 = 120; % 120Hz分量
signal = sin(2*pi*f1*t) + 0.5*cos(2*pi*f2*t);% 设置VMD参数
alpha = 2000; % 平衡参数
tau = 0; % 无噪声松弛
K = 5; % 分解2个模态
DC = false; % 无直流分量
init = 1; % 均匀初始化
tol = 1e-6; % 收敛容差% 执行VMD分解
[u, u_hat, omega] = VMD(signal, fs, alpha, tau, K, DC, init, tol);% 显示结果
disp('估计的中心频率 (Hz):');
disp(omega);% 绘制结果
figure;
subplot(K+1, 1, 1);
plot(t, signal);
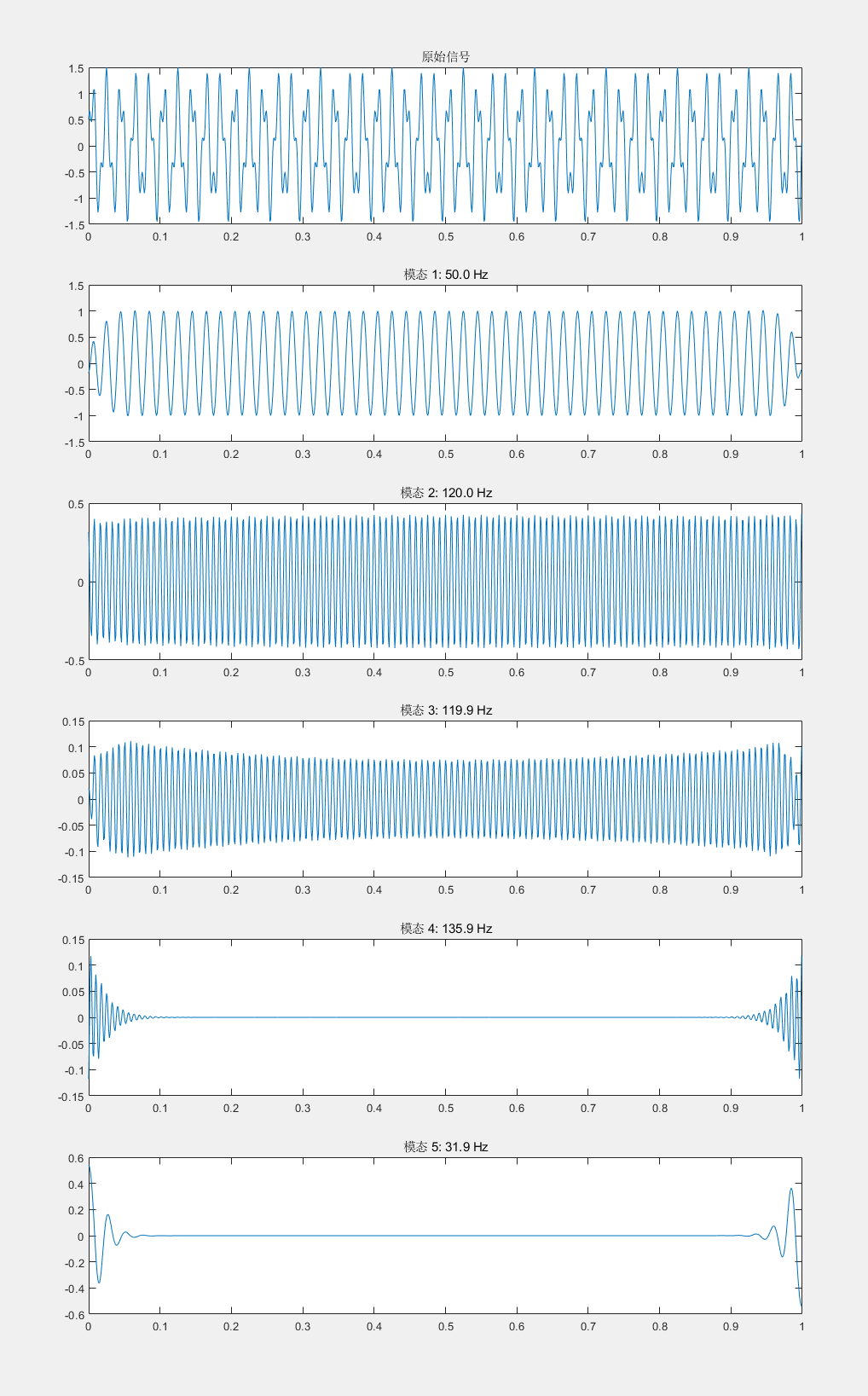
title('原始信号');for k = 1:Ksubplot(K+1, 1, k+1);plot(t, u(k, :));title(sprintf('模态 %d: %.1f Hz', k, omega(k)));
end可视化: