当前位置： 首页 > news >正文

机器学习 SVM支持向量机

news 2025/8/11 13:09:09

目录

一.什么是支持向量机

直观理解分类边界：从 “分割线” 到 “超平面”

二.什么是支持向量

三.逻辑回归与支持向量机的对比

四.支持向量机的核心思想

五.异常点的影响与解决方法

1.影响

2.什么是惩罚因子C

3.解决方案

六.常见的核函数类型

七.支持向量机的优缺点

1.优点

2.计算依赖

3.缺点

八.SVC分类模型关键参数与训练后的模型属性

1.关键参数

2.训练后的模型属性

九.SVM 实战：用 scikit-learn 实现分类任务  鸢尾花的分类

1.读取数据，csv文件并无列名，header设为None

2.划分数据集

3.创建模型

4.训练模型并预测

5.完整代码

十.总结

一.什么是支持向量机

支持向量机（SVM）是一种二分类模型，其核心思想是：在特征空间中找到一个最优分类边界，使得两类数据之间的间隔最大化。这个 “间隔” 指的是分类边界到最近的样本点的距离，而这些距离分类边界最近的样本点被称为 “支持向量”（Support Vectors）—— 它们是决定分类边界位置的关键数据点。

直观理解分类边界：从 “分割线” 到 “超平面”

  • 在二维空间中，分类边界是一条直线；
  • 在三维空间中，分类边界是一个平面；
  • 在更高维的特征空间中，分类边界被称为 “超平面”（Hyperplane）。

SVM 的目标就是找到这样一个分类边界，使得两类数据被完美分隔，且距离分类边界最近的样本点到分类边界的距离最大（即 “最大间隔分类边界”）。

二.什么是支持向量

支持向量是距离分类边界最近的数据点，这些点决定了分类边界的位置。

它们决定了分类边界的位置和方向。在模型训练完成后，其他样本点的位置对分类边界不再产生影响 —— 这意味着 SVM 对冗余数据不敏感，计算效率较高

三.逻辑回归与支持向量机的对比

  • 逻辑回归的目标是找到一条线将两类数据划分开，但可能存在局部极值点问题，且不保证找到最优划分线。
  • 支持向量机（SVM）的目标是找到一条最优线，使得距离最近的数据点（支持向量）尽可能远，从而提高分类准确性。

四.支持向量机的核心思想

  • 最大间隙：SVM 追求分类器与最近数据点之间的最大距离即使软间隔最大化。
  • 高维映射：通过核函数将低维数据映射到高维空间，使得原本线性不可分的数据在高维空间中线性可分。
  • 超平面：在高维空间中，分类器表现为超平面（如二维为线，三维为平面，更高维为超平面）。

关键术语解释：

  • 分类器：用于划分数据的线或超平面。
  • 核函数：将低维数据映射到高维空间的函数（如线性核、多项式核等）。
  • 支持向量：距离分类器最近的、影响分类决策的数据点。

五.异常点的影响与解决方法

1.影响

异常数据可能导致分割线偏移，使间隔（软间隔）变小，引发过拟合问题。即严格分类所有点（包括异常点）会导致间隔过小，泛化能力差

2.什么是惩罚因子C

惩罚因子是控制数据点进入的幅度，C越大分类越严格（不容有误），C越小则更宽松（允许错误点进入）。

3.解决方案

引入松弛因子（惩罚因子C），允许少数点进入间隔内，减少异常点干扰。即在原目标函数中加入松弛项，平衡分类准确性与间隔宽度。

六.常见的核函数类型

  • 线性核：直接低维计算，不提升维度。
    • 表达式：k(x, y) = x · y（向量点积）
    • 适用场景：线性可分数据，或特征维度较高的场景（如文本分类，特征维度通常为词袋维度）。
    • 优势：计算速度快，解释性强，不易过拟合。
  • 多项式核（如γ(xᵢxⱼ+c)ⁿ）
    • 表达式：k(x, y) = (γ · x · y + r)^d
    • 超参数：γ（核系数）、r（常数项）、d（多项式次数）。
    • 适用场景：数据具有明显多项式分布特征时（如二维空间中呈曲线分布的数据）。
    • 注意：d过大时易过拟合，需结合交叉验证调整。
  • 高斯核（或径向基函数核RBF，默认核函数）：
    • 表达式：k(x, y) = exp(-γ · ||x - y||²)
    • 超参数：γ控制核函数的 “宽度”——γ越大，核函数越 “窄”，模型对局部数据敏感（易过拟合）；γ越小，核函数越 “宽”，模型泛化能力越强。
    • 适用场景：非线性数据，且数据分布未知时的首选核函数。它能灵活拟合复杂的非线性关系，是实际应用中使用最广泛的核函数。
  • sigmoid核：较少单独使用，有时用于模拟神经网络，可用于构建非线性模型。

七.支持向量机的优缺点

1.优点

  • 泛化能力强：通过最大化间隔，SVM 在小样本数据集上表现优异，不易过拟合。
  • 对高维数据友好：即使特征维度远大于样本数量，SVM 仍能有效工作（如文本分类）。
  • 对噪声不敏感：支持向量仅关注关键样本，冗余数据不影响模型。
  • 核函数机制灵活：通过核函数轻松处理非线性问题，无需手动设计高维特征。

2.计算依赖

计算的复杂度由支持向量数量决定，而非数据维度。

3.缺点

  • 计算复杂度高：训练时间随样本数量增加而显著增长，不适合超大规模数据集（通常样本数超过 10 万时需谨慎使用）。
  • 调参复杂：核函数选择、C和γ等超参数对模型效果影响大，需大量交叉验证。对参数和核函数的选择敏感，若选择不当会影响结果
  • 多分类支持较弱：SVM 本质是二分类模型，多分类任务需通过 “一对多” 或 “一对一” 策略间接实现。
  • 对缺失值敏感：数据预处理需严格处理缺失值，否则会影响核函数计算。

八.SVC分类模型关键参数与训练后的模型属性

源码如下

1.关键参数

  • 惩罚因子 C(软间隔)：
    • 控制异常数据是否作为支持向量。
    • C值越大，分类越严格（不容有误）；C值越小，分类越宽松（允许异常点进入）。
    • 建议通过交叉验证选择（如0.01、0.1、1、100等）。
  • 核函数（kernel）：
    • 默认选择RBF（径向基/高斯核函数）。
    • 其他选项：线性核函数、多项式核函数、sigmoid核函数。
  • gamma：
    • 控制核函数中正态分布的“高矮胖瘦”，影响数据映射位置。
    • 默认值为特征数的倒数（如10个特征时gamma=0.1）。
  • degree：
    • 仅在使用多项式核函数时需设置，其他情况下忽略。

2.训练后的模型属性

可获取支持向量svm.support_vectors_

系数svm.coef_[0]

及截距项svm.intercept_[0]等结果

九.SVM 实战：用 scikit-learn 实现分类任务  鸢尾花的分类

iris.csv的部分内容如下：第一列为编号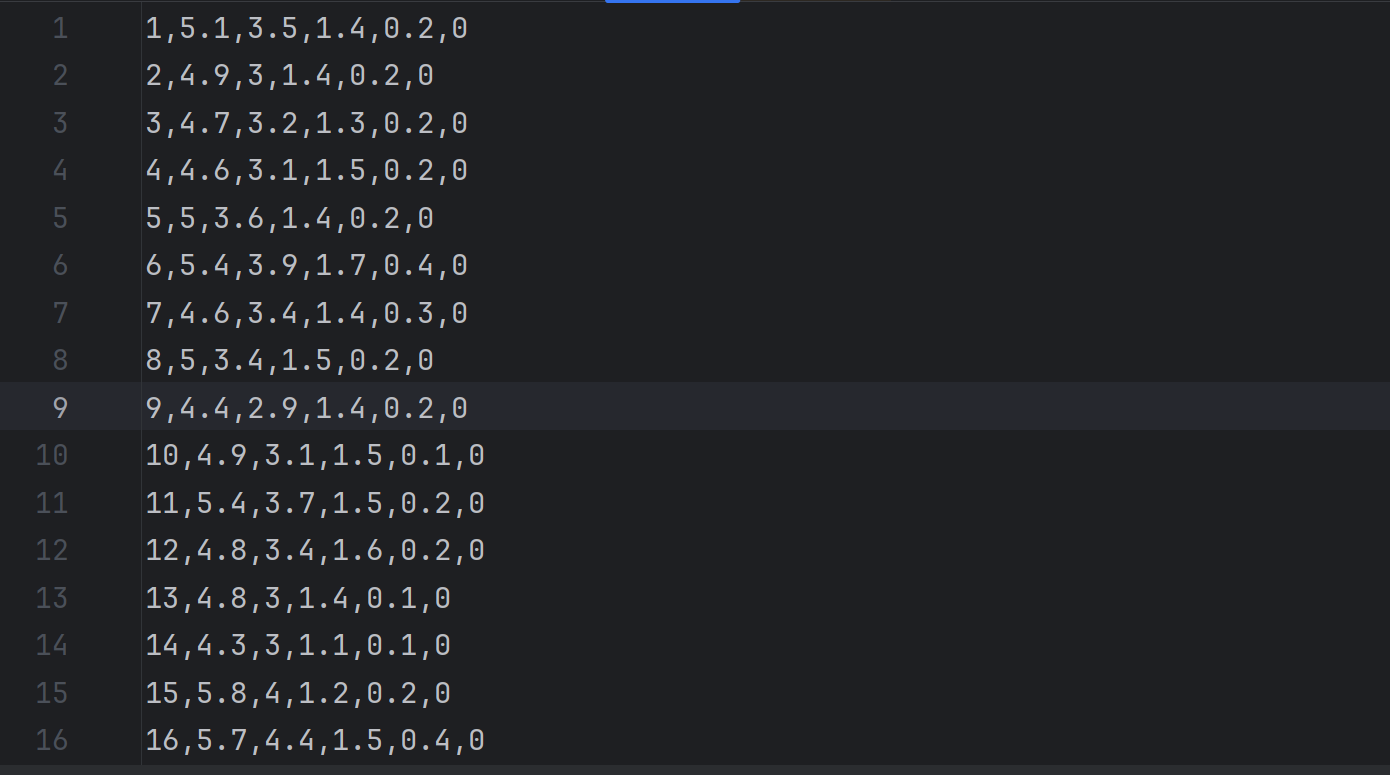

1.读取数据，csv文件并无列名，header设为None

from sklearn.svm import SVC
import pandas as pd
from  sklearn import metrics
from sklearn.model_selection import train_test_splitdata=pd.read_csv('iris.csv',header=None)

2.划分数据集

X=data.iloc[:,1:5]
y=data.iloc[:,-1]
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.2,random_state=100)

3.创建模型

使用线性核函数（kernel='linear'）和严格参数（C=float('inf')）进行SVM训练，确保无异常点进入软间隔。

svm=SVC(kernel='linear',C=float('inf'),random_state=0)

4.训练模型并预测

svm.fit(train_x,train_y)
predicted=svm.predict(test_x)
print(metrics.classification_report(test_y,predicted))precision    recall  f1-score   support0       1.00      1.00      1.00        111       1.00      1.00      1.00         9accuracy                           1.00        20macro avg       1.00      1.00      1.00        20
weighted avg       1.00      1.00      1.00        20

5.完整代码

import numpy as np
from sklearn.svm import SVC
import pandas as pd
from  sklearn import metrics
from sklearn.model_selection import train_test_splitdata=pd.read_csv('iris.csv',header=None)X=data.iloc[:,1:5]
y=data.iloc[:,-1]
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.2,random_state=100)
svm=SVC(kernel='linear',C=float('inf'),random_state=0)
svm.fit(train_x,train_y)
predicted=svm.predict(test_x)
print(metrics.classification_report(test_y,predicted))

十.总结

支持向量机（SVM）是一种基于统计学习理论的经典算法，其核心思想是通过最大化间隔找到最优超平面，结合核函数机制有效处理非线性问题。尽管在超大规模数据集上的训练效率不如深度学习模型，但 SVM 在小样本、高维特征的分类任务中仍具有不可替代的优势。

使用 SVM 时需注意：

  • 根据数据线性性选择合适的核函数（优先尝试线性核和 RBF 核）。
  • 通过交叉验证调整C（惩罚系数）和γ（核系数）等超参数。
  • 对数据进行标准化预处理（核函数对特征尺度敏感）。

掌握 SVM 不仅能帮助解决实际分类问题，更能深入理解机器学习中 “间隔最大化”“核技巧” 等核心思想，为后续学习更复杂的模型打下基础。

http://www.xdnf.cn/news/1262827.html

相关文章：

  • 【Git】企业级使用
  • 50系显卡ubuntu20.04安装显卡驱动，解决gazebo不调用显卡的问题
  • 【前端后端部署】将前后端项目部署到云服务器
  • 零成本建站：将 Windows 电脑变身为个人网站服务器
  • MetaBit基金会加码投资图灵协议，深化去中心化金融与元宇宙生态合作
  • windows 上编译PostgreSQL
  • 客户端攻击防御：详解现代浏览器安全措施
  • 【unitrix数间混合计算】2.4 二进制整数标准化处理(src/number/normalize/int_normalize.rs)
  • seo-使用nuxt定义页面标题和meta等信息
  • Nearest Smaller Values(sorting and searching)
  • 3-防火墙
  • 2025年最新Java后端场景题＋八股文合集（100w字面试题总结）
  • 华清远见25072班C语言学习day5
  • 基于Spring Boot的Minio图片定时清理实践总结
  • Ideogram：优秀的在线AI绘画平台
  • 【代码随想录day 15】 力扣 110.平衡二叉树
  • HTTP 请求返回状态码和具体含义？200、400、403、404、502、503、504等
  • 机械学习--SVM 算法
  • 用LaTeX优化FPGA开发：结合符号计算与Vivado工具链（二）
  • 华为网路设备学习-28（BGP协议 三）路由策略
  • Android Studio第一个kotlin项目“Hello Android”
  • kafak
  • windows自动获取wsl IP，并开启端口转发。
  • 【代码随想录day 14】 力扣 111.二叉树的最小深度
  • Axure基于中继器实现的组件库(导航菜单、动态表格)
  • Array Description(Dynamic programming)
  • 在发布应用程序内测时如何选择合适的分发上架方式？
  • Git 基础操作笔记（速查）
  • 视频遥测终端机是什么，其工作原理和应用领域
  • 高校合作 | 世冠科技联合普华、北邮项目入选教育部第二批工程案例