字符串匹配--KMP算法
KMP 算法主要是用于解决字符串匹配问题,也就是我们常说的查找子串问题。
KMP 代码实现相对较为简单,10 行代码足矣,但是算法原理比较复杂,需要大家下点功夫去学习,需要更多的练习。
KMP 是字符串处理的经典算法,在比赛中出场次数较高,所以我们要克服困难,面对算法,学会它。
知识点
KMP 算法知识点讲解
KMP 算法的应用
KMP 算法
KMP 算法是一个非常著名且高效的字符串匹配算法,大学中的很多教材对于 KMP 的算法讲解或是浅尝辄止,或者是讲的不是那么通透。像作者学习的时候,也被 Knuth、Morris、Pratt 三位创作者劝退。
对于 KMP 算法的学习,作者的学信心的是通过手推每一次算法的过程,熟悉算法的实现方式,像是网上说的十行代码搞定 KMP 算法,通过背模板的方式都是不可取的。
学习算法的过程首先是逻辑层面其次是代码层面。
接下来我们将先讲解 KMP 算法的逻辑原理,然后在讲解算法的实现。
术语解释
我们讲的官方一点,这样方便大家学习更深层次的算法。
主串(目标串): 简单来说就是被搜索的字符串,一般来说就是那个长的。
模式串:被匹配,是查找的目标。
算法目标:字符串中的模式定位问题,简单来说就是查找子串,在主串中查找匹配模式串。这一类的算法,又被我们称为模式匹配算法。
说到模式匹配算法,就绕不开暴力,暴力算法的也是有名字的,叫 BF 算法。
接下来我们从 BF 算法开始学习,抛砖引玉的研习 KMP 算法。
BF算法:
S=input()
T=input()
count=0
for i in range(len(S)):z=ifor j in range(len(T)):if S[z]==T[j]:z+=1else:breakif (z-i)==len(T)-1:count+=1
print(count)毫无疑问,这个代码无疑是完全正确的,但从时间复杂度方面考虑的话,他的时间复杂度无疑是O(n*m),那我们思考一下,有什么方法可以优化一下呢?
我们发现 BF 算法每次 t 匹配失败都往后移动一个位置,有没有一种可能,在一次匹配中我们能判断移动几次,或者说我们能不能知道向后移动几个是一定不能找到正确答案,然后进行剪枝。
沿着这个思路我们开始考虑一下 KMP 算法。
KMP 算法详解
写在代码最前面,KMP 算法中根据编译器版本不同,有的编译器可能开不出 next 数组,大家可以改成 Next 或者 nextt 等,换个名字。
对于 KMP 大家都知道要求 next 数组,所有教科书也都会告诉你 Next 数组怎么求,然后根据 next 数组怎么执行 KMP 算法。
本文将从 Next 数组转移的原理出发,力求让大家理解,当然 KMP 算法仍是一个模板算法,可以记住代码,不去理解,遇见题目能够写出模板即可。
如果按照正常 BF 算法做字符串匹配的话,我们能够写出如下代码
static String T="ABCDEFG";
static String P="FG";static int BF(String s,String p) {int i = 0; //主串中的位置int j = 0; // 模式串中的位置int sLen = s.length();int pLen = p.length();while (i < sLen && j < pLen) {if (s.charAt(i)==p.charAt(j)) { // 当两个字符相同,就比较下一个i++;j++;} else {i = i - j + 1;j = 0; //一旦不匹配,模式串位置j回退到0;}// System.out.println(i+":"+j);}if (j == pLen)return (i - j); //主串中存在该模式返回下标号elsereturn -1; //主串中不存在该模式
}public static void main(String[] args) {System.out.println(BF(T,P));
}
T = "老师上课讲的题目很简单"P = "简单"def BF(s, p):i = 0 # 主串中的位置j = 0 # 模式串中的位置sLen = len(s)pLen = len(p)while i < sLen and j < pLen:if s[i] == p[j]:i += 1j += 1else:i = i - j + 1j = 0if j == pLen:return i - jelse:return -1print(BF(T, P))我们看到 i 每次匹配不成功,就回到了初始位置,再向后移动一位。
对于正确性,上面的算法确实是毫无疑问,没有任何问题。但是对于效率上面的算法,确实非常低劣。
而我们将会使用 KMP 算法解决上面这种低效回退的问题。
KMP 算法的核心思想是,利用已经匹配过的这一部分有效的信息,保持主串位置 i 的值不变,去修改模式串的位置 j 的值。
即 KMP 算法就是告诉我们这个 j 该如何去改变。
在讲 Next 数组之前,我们先来讨论一下前后缀的概念。
字符串前后缀:
前缀:
符号串左部的任意子串(或者说是字符串的任意首部),在 KMP 算法中使用的是“真”前缀,即不包含自己前缀。
简单记忆方式: 前缀要找除了自己,且从头开始的所有子串。
后缀:
符号串右部的任意子串(或者说是字符串的任意尾部),在 KMP 算法中使用的是“真”后缀,即不包含自己后缀。
简单记忆方式: 前缀要找除了自己,且以最后一个字符结尾的所有子串。
举例:
| 字符串 | 真前缀 | 真后缀 |
|---|---|---|
| a | 无 | 无 |
| ab | a | b |
| aba | a,ab | a,ba |
| abaa | a,ab,aba | a,aa,baa |
| abaab | a,ab,aba,abaa | b,ab,aab,baab |
| abaabc | a, ab,aba,abaa,abaab | c,bc,abc,aabc,baabc |
| abaabca | a, ab,aba,abaa,abaaab,abaabc | c,bc,abc,aabc,baabc,baabca |
求 Next 数组前,我们还要去了解一下最长公共前后缀,他的长度对于 KMP 的 Next 数组的计算有着紧密的联系。
最长公共前后缀:
| 字符串 | 真前缀 | 真后缀 | 最长公共真前后缀 |
|---|---|---|---|
| a | 无 | 无 | 无 |
| ab | a | b | 无 |
| aba | a,ab | a,ba | a |
| abaa | a,ab,aba | a,aa,baa | a |
| abaab | a,ab,aba,abaa | b,ab,aab,baab | ab |
| abaabc | a, ab,aba,abaa,abaab | c,bc,abc,aabc,baabc | 无 |
| abaabca | a, ab,aba,abaa,abaaab,abaabc | c,bc,abc,aabc,baabc,baabca | a |
后面的文中将真省略,大家注意。
如果设模式串 P = "abaabca" ,那我们可以得到以某个位置结尾的子串的最长公共前后缀长度。
| 字符串 | 结尾 | 最长公共前后缀长度 | 最长公共前后缀 |
|---|---|---|---|
| a* | a | 0 | 无 |
| ab* | b | 0 | 无 |
| aba* | a | 1 | a |
| abaa* | a | 1 | a |
| abaab* | b | 2 | ab |
| abaabc* | c | 0 | 无 |
| abaabca | a | 1 | a |
我们可以得出以下表格:
| 结尾 | a | b | a | a | b | c | a |
|---|---|---|---|---|---|---|---|
| 最长公共前后缀长度 | 0 | 0 | 1 | 1 | 2 | 0 | 1 |
对于 Next 数组将整体向右移动一位后,在左侧补-1。
| 结尾 | a | b | a | a | b | c | a |
|---|---|---|---|---|---|---|---|
| Next | -1 | 0 | 0 | 1 | 1 | 2 | 0 |
Next 数组的含义:
对于模式串"abaabca"而言
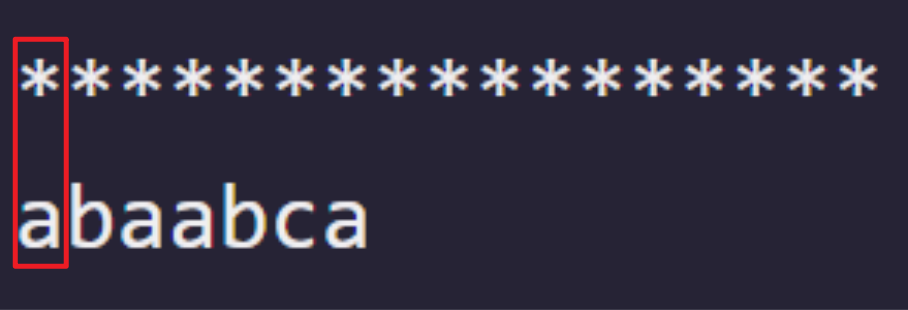
出现这种从第 1 位就匹配出错的情况,即使通过人工我们不能找到任何优化方式,于是只能将模式串右移。
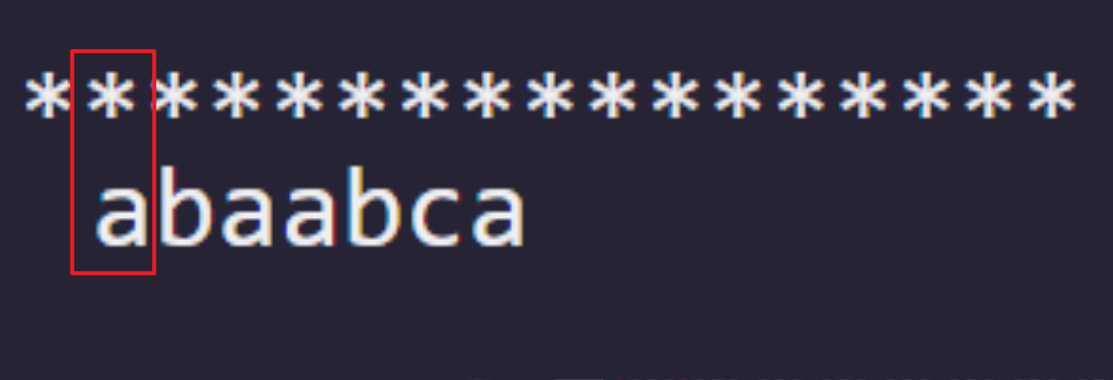
恰好模式串的 -1 的位置正好置于主串的 i 位置,这就是 next 的第一位补-1 的原因。
我们再看第二种情况,部分匹配成功的情况。
仍对于模式串"abaabca"而言:
设主串为"abaaefaged",那么会有:
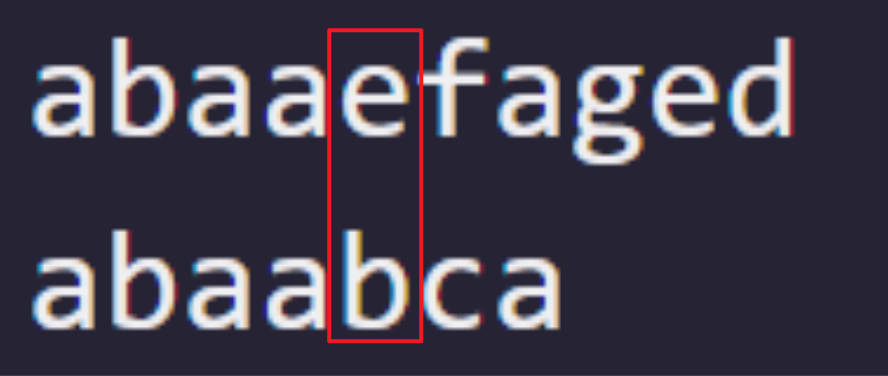
在主串的 i=4 位置,模式串 j=4 的位置发生了不匹配。
我们通过最优人工移动可以得到:
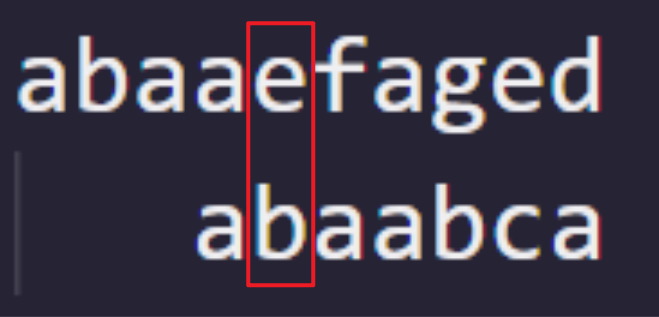
恰好与主串 i 位置对应的值是模式串的 1 号位置。
那么与我们计算出的 Next 的数组值相同。
重点来了,我们说一下为什么可以这么神奇!!!
原因:
由于我们通过 next 数组计算,而 next 数组来源于最长公共前后缀的长度,那么为什么最长公共前后缀就能计算出,转移目标呢?
假设某个字符串 s 的最长共前后缀为 X="abcd...",那么这个字符串一定是一下结构,开头是 X 结尾是 X 中间可能会有重叠,匹配到 s 的最后一个字符失败后,那我们知道 X 肯定是匹配成功了,因为 X 不包含最后一个字符。
既然我们知道 X 匹配成功,那么我们一定知道,在主串中一定是从 i 位置开始且一定有一个 X 与模式串中的 X 匹配成功。
如下,点为省略号:
i
T=........X.......
S= X.......j
而我们又已知,字符串 s 一定有一个后缀 X,那么我们直接用 s 的后缀 X 去匹配主串的 X,且 X 是最长公共前后缀,那么我们就完成了最优的转移。
当 s 是模式串的从头开始的子串时,就可以得到从某一个字符不匹配时的转移情况。
基本原理已经讲清楚了,我们开始说 KMP 算法。
KMP 算法框架和 BF 大致相似,根据上面的分析,对于字符串的比对我们分为三种。
T[i]==P[j] 的情况
此时,两字符相同应该继续比对所以:
i=i+1j=j+1T[i]!=P[j] 的情况
此时,两字符不相同,j 应该根据 next 数组进行转移,所以:
j=next[j]j=-1 的情况
因为,j=next[j],且 next 第一位为 -1 即出现了第一位就匹配失败的情况,那我们应该做的是,是的模式串的开头向后移动,即:
j=j+1那么 j 对应 i 的位置也变成了 i+1 所以:
i=i+1那么与情况 1 相同,我们一同考虑。
**!!!!!!**至此,KMP 算法整体思路完成。
我们可以得到一下 KMP 的模板:
int KMP(int sStart,String s,String p)
{/*tStart 从主串的哪个位置开始,从头开始为0s 主串p 模式串*/int i=sStart; //从主串的sStart位置开始int j=0;int sLen = s.length();int pLen = p.length();while (i < sLen && j < pLen){//①如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++if(j==-1||s.charAt(i)==p.charAt(j)){i++; //继续对下一个字符比较j++; //模式串向右滑动}else{j = next[j];//②如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]//next[j]即为j所对应的next值}}if (j == pLen)return (i-j); //主串中存在该模式返回下标号elsereturn -1; //主串中不存在该模式
}
def KMP(sStart, s, p):# tStart 从主串的哪个位置开始,从头开始为0# s 主串# p 模式串i = sStart # 主串中的位置j = 0 # 模式串中的位置sLen = len(s)pLen = len(p)while i < sLen and j < pLen:if j==-1 or s[i] == p[j]:# 如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++i += 1j += 1else:j = next[j]# 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = nextt[j]# next[j]即为j所对应的next值if j == pLen:return i - jelse:return -1KMP 算法讲解至此结束,但是我们漏下了一个东西,那就是 Next 数组的计算。
由于 Next 数组计算优化较多,且涉及部分编译原理的知识,我给大家一种求解 Next 数组的模板,大家理解即可:
def GetNext(p):pLen = len(p)next[0] = -1k = -1j = 0while j < pLen - 1:# p[k]表示前缀,p[j]表示后缀if k == -1 or p[j] == p[k]:j += 1k += 1next[j] = kelse:k = next[k]
static void Getnext(String p) {int pLen = p.length();next[0] = -1;int k = -1;int j = 0;while (j < pLen - 1) {//p[k]表示前缀,p[j]表示后缀if (k == -1 || p.charAt(j) == p.charAt(k)) {++k;++j;next[j] = k;} else {k = next[k];}}
}至此 KMP 算法神功大成,我们得以写出一下模板。
KMP 模板
public class Main {static String T = "ABCDEFG";static String P = "AB";static int[] next = new int[100005];static void Getnext(String p) {int pLen = p.length();next[0] = -1;int k = -1;int j = 0;while (j < pLen - 1) {//p[k]表示前缀,p[j]表示后缀if (k == -1 || p.charAt(j) == p.charAt(k)) {++k;++j;next[j] = k;} else {k = next[k];}}}static int KMP(int sStart, String s, String p) {/*tStart 从主串的哪个位置开始,从头开始为0s 主串p 模式串*/int i = sStart; //从主串的sStart位置开始int j = 0;int sLen = s.length();int pLen = p.length();while (i < sLen && j < pLen) {//①如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++if (j == -1 || s.charAt(i) == p.charAt(j)) {i++; //继续对下一个字符比较j++; //模式串向右滑动} else {j = next[j];//②如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = nextt[j]//nextt[j]即为j所对应的nextt值}}if (j == pLen)return (i - j); //主串中存在该模式返回下标号elsereturn -1; //主串中不存在该模式}public static void main(String[] args) {Getnext(P);System.out.println(KMP(0, T, P));}
}
T = "ABCDEFG"P = "FG"next = [0 for i in range(10005)]def GetNext(p):pLen = len(p)next[0] = -1k = -1j = 0while j < pLen - 1:# p[k]表示前缀,p[j]表示后缀if k == -1 or p[j] == p[k]:j += 1k += 1next[j] = kelse:k = next[k]def KMP(sStart, s, p):# tStart 从主串的哪个位置开始,从头开始为0# s 主串# p 模式串i = sStart # 主串中的位置j = 0 # 模式串中的位置sLen = len(s)pLen = len(p)while i < sLen and j < pLen:if j==-1 or s[i] == p[j]:# 如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++i += 1j += 1else:j = next[j]# 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = nextt[j]# next[j]即为j所对应的next值if j == pLen:return i - jelse:return -1if __name__ == '__main__':GetNext(P)print(KMP(0, T, P))