Day25-对称二叉树-
对称二叉树
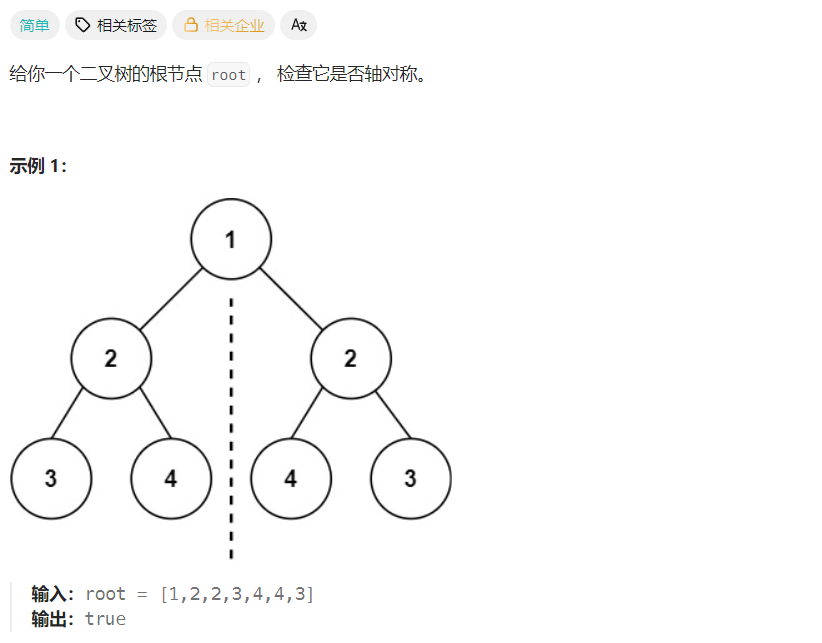
递归法:自己实现一个比较左右节点的函数,然后去递归实现就好了,不过需要注意的是在判断的时候要镜像的判断!
bool compare(struct TreeNode* left,struct TreeNode* right){if(left == NULL && right == NULL) return true;//如果左右都为空那么只有根节点,一定是对称的else if(left != NULL && right == NULL) return false;else if(right != NULL && left == NULL) return false;else if(right->val != left->val) return false;bool outside = compare(left->left,right->right);bool inside = compare(right->left,left->right);bool isSame = outside && inside;return isSame;}
bool isSymmetric(struct TreeNode* root) {if(root == NULL) return true;return compare(root->left,root->right);
}使用C语言实现的,C++也一样。
迭代法呢?就是层序遍历!左右节点入栈\队列,然后创建一个新的指针只想他们,如果不是空节点就continue,但凡有一个节点为空或者对应的值不一样直接返回false。
while (!que.empty()) { // 接下来就要判断这两个树是否相互翻转TreeNode* leftNode = que.front(); que.pop();TreeNode* rightNode = que.front(); que.pop();if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是对称的continue;}
// 左右⼀个节点不为空,或者都不为空但数值不相同,返回falseif ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {return false;}
……
}C++写的,C语言就不同了,C语言使用数组去模拟队列
bool isSymmetric(struct TreeNode* root) {if (root == NULL) return true;// 用数组模拟队列struct TreeNode* queue[1000];int left = 0, right = 0;// 初始放入左右子树queue[right++] = root->left;queue[right++] = root->right;while (left < right) {struct TreeNode* leftNode = queue[left++];struct TreeNode* rightNode = queue[left++];if (!leftNode && !rightNode) continue;if (!leftNode || !rightNode || leftNode->val != rightNode->val)return false;// 注意对称入队顺序queue[right++] = leftNode->left;queue[right++] = rightNode->right;queue[right++] = leftNode->right;queue[right++] = rightNode->left;}return true;
}二叉树的最大深度
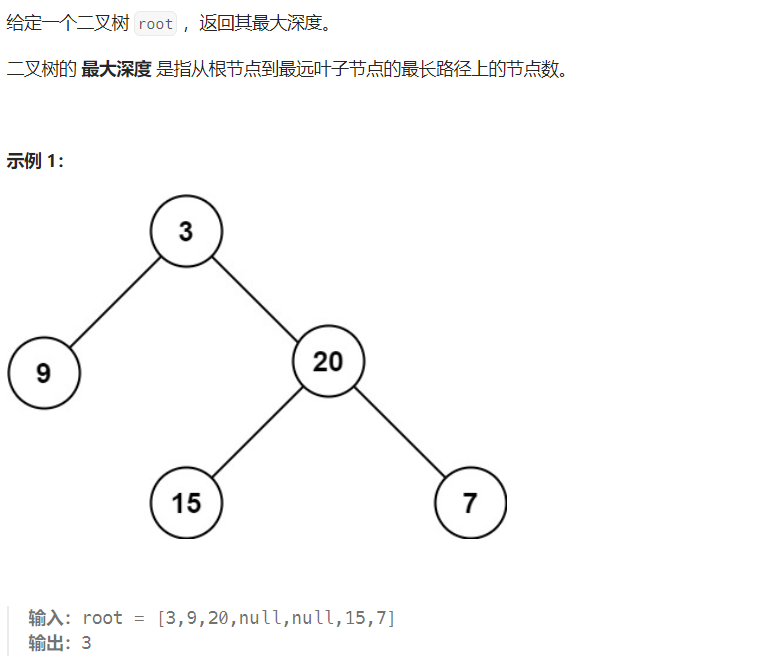
说到这,要学习一下什么是二叉树的最大深度和最大高度。
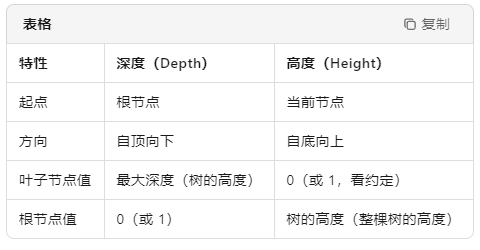
根节点的⾼度就是⼆叉树的最⼤深度
-
深度(Depth):从 根 往下数,节点所在的层数(根为第 0 或 1 层,看约定)。
-
高度(Height):从 节点 往下数,到最远叶子节点的路径长度(叶子节点高度为 0)

递归法:使用三部曲
① 递归终止条件
② 递归参数和返回值
③ 递归逻辑是什么?
把左右节点都递归一下求最大深度+1就好了
int maxDepth(struct TreeNode* root) { // 求树的高度/最大深度if (!root) return 0; // 空节点高度为 0int left_height = maxDepth(root->left);int right_height = maxDepth(root->right);return (left_height > right_height ? left_height : right_height) + 1;
}迭代法的话代码就长一点了,但是感觉会比较直观,
int maxDepth(struct TreeNode* root) { // 求树的高度/最大深度if(root == NULL) return 0;struct TreeNode *que[1000];int left = 0,right = 0,depth = 0;que[right++]=root;while(left<right){int size = right - left;depth++;for(int i = 0;i<size;i++){struct TreeNode *node = que[left++] ;//从队列头开始依次把所有节点的子节点加入队列if(node->left) que[right++] = node->left;if(node->right) que[right++] = node->right;}}return depth;
}C语言实现,其实C++也一样的了,不过使用层序遍历要注意一下,C语言需要使用数组去实现。
不过还是看一下代码随想录的题解,特别细。
