当前位置：首页 > news >正文

DoRA详解：从LoRA到权重分解的进化

news 2025/8/1 8:48:26

DoRA是一种用于大语言模型（LLM）微调的技术，全称为 "Weight-Decomposed Low-Rank Adaptation"（权重分解的低秩自适应）。它是对现有微调方法（如 LoRA）的改进，旨在更高效地调整模型参数，同时减少计算资源消耗。

论文链接：https://arxiv.org/pdf/2402.09353

1. 概括

2. 详解

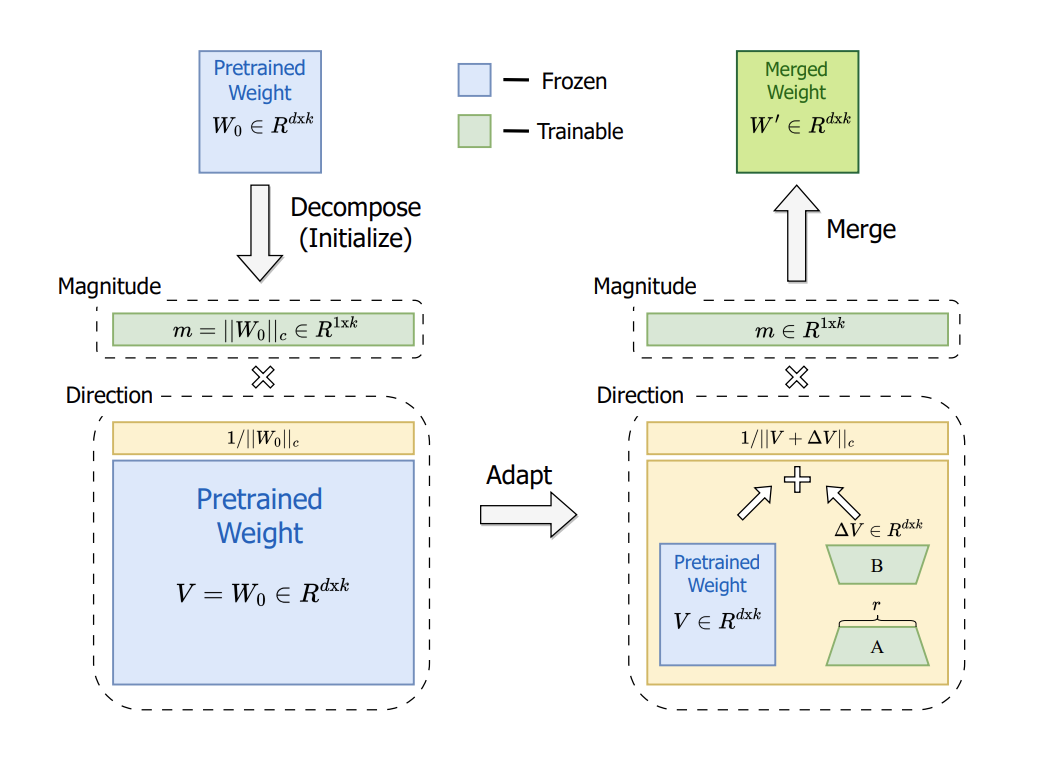
核心思想：DoRA 通过分解预训练模型的权重矩阵，将其拆分为幅度（magnitude）和方向（direction）两部分，分别进行低秩（low-rank）调整。这种分解方式能更精细地控制参数更新，提升微调效果。
与 LoRA 的关系：
- LoRA（Low-Rank Adaptation）：通过在原始权重旁添加低秩矩阵（而非直接修改权重）来微调模型，减少参数量。
- DoRA：在 LoRA 基础上引入权重分解，进一步优化参数更新的方向和幅度，提高训练稳定性。

1. 权重矩阵分解

输入与目标

输入：预训练权重矩阵 $W_0\in \mathbb{R}^{d\times d}$ （蓝色矩形）。
目标：将 $W_0$ 分解为幅度(Magnitude) $m$ 和方向(Direction) $V$ 。

✅分解操作

1.1 计算幅度 $m$

$m=\left \| W_0 \right \|_c\in \mathbb{R}^{d\times d}$

$\left \| \cdot \right \|_c$ 表示矩阵的 C范数（具体可能是列范数或Frobenius范数，需根据上下文确定）。
幅度 $m$ 是标量或对角矩阵（图中浅绿色矩形），表示权重的整体缩放因子。

1.2 计算方向 $V$

$V=\frac{W_0}{\left \| W_0 \right \|_c}\in \mathbb{R}^{d\times d}$

方向（浅黄色矩形）是归一化后的权重矩阵，保留原始权重的“方向”信息。

1.3 验证分解

重构公式：
说明：分解后可通过幅度和方向重新组合得到原始权重，确保数学等价性。
$V$ 的范数 $\left \| V \right \|_c=1$ （单位范数）。

2. 微调训练

2.1 方向矩阵 $V$ 的低秩适应（LoRA）

低秩分解
- 对方向矩阵应用标准 LoRA：
  - $\bigtriangleup V=BA\in \mathbb{R}^{d\times d}$
  - 其中 $A\in \mathbb{R}^{d \times r},B\in \mathbb{R}^{r\times d}, r\ll d$
- A和 B是可训练的低秩矩阵（绿色矩形），r为秩（超参数）。
更新方向矩阵
- 微调后的方向矩阵：
  - $V'=V+\bigtriangleup V=V+BA$

2.2 幅度 $m$ 的训练

幅度 $m$ 直接作为可训练参数（绿色矩形），通过梯度下降调整。
- $W'=m\cdot \frac{V}{\left \| V \right \|_c}=m\cdot \frac{V+BA}{\left \| V+BA \right \|_c}$
- 通过归一化确保方向矩阵的单位性。

可训练参数：

低秩矩阵 A、B（方向调整）。

幅度 m（全局缩放调整）。

冻结参数：

原始方向 V（仅用于初始化，不更新）。

3. 代码

伪代码如下

import torch
import torch.nn as nnclass DoRALayer(nn.Module):def __init__(self, d, r):super().__init__()# 初始化预训练权重 W0self.W0 = nn.Parameter(torch.randn(d, d))# 分解为幅度和方向self.m = nn.Parameter(torch.norm(self.W0, dim=0))  # 幅度（可训练）self.V = self.W0 / torch.norm(self.W0, dim=0)      # 方向（冻结）# LoRA 参数self.A = nn.Parameter(torch.randn(d, r))self.B = nn.Parameter(torch.zeros(r, d))def forward(self, x):V_prime = self.V + torch.matmul(self.B, self.A)  # V + BAV_prime_norm = torch.norm(V_prime, dim=0)W_prime = self.m * (V_prime / V_prime_norm)       # 合并权重return torch.matmul(x, W_prime.T)