数据结构 二叉树(3)---层序遍历二叉树
在上篇文章中我们主要讲了关于实现二叉树的内容,包括遍历二叉树,以及统计二叉树等内容。而
在这篇文章中我们将详细讲解一下利用队列的知识实现层序遍历二叉树。
那么层序遍历是什么?以及利用队列遍历二叉树又是怎么遍历的?下面让我们一起带着这些问题深
入研究:
1. 什么是层序遍历?
我们仍然以之前使用过的二叉树为例。
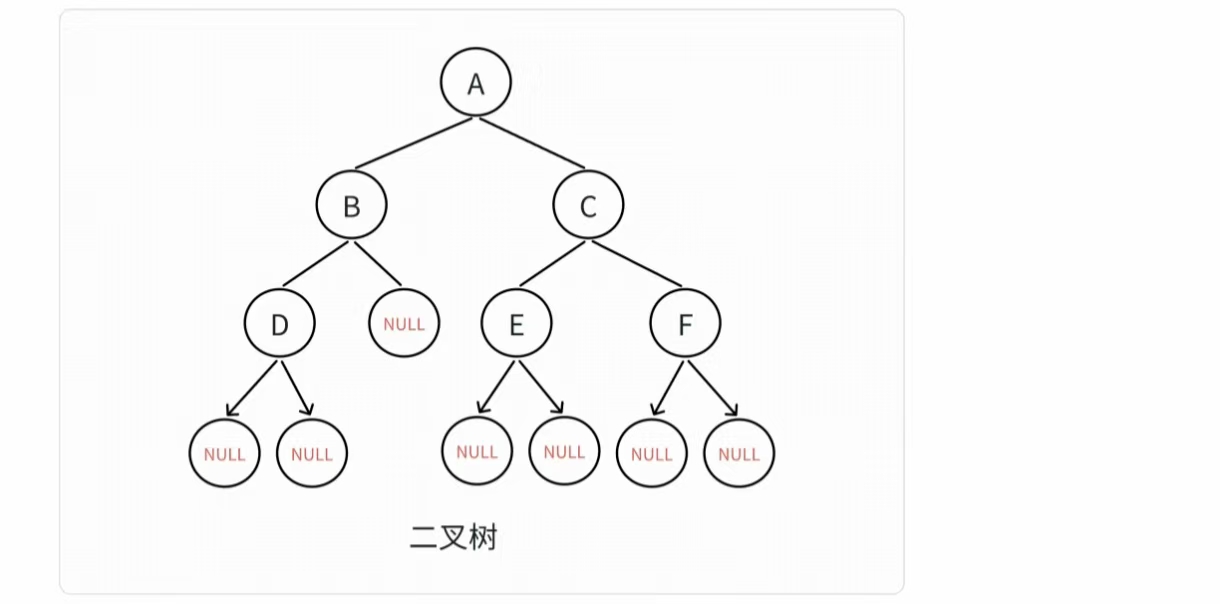
对于二叉树而言 : 层序遍历二叉树,简单说就是按“层次”访问节点:从根节点开始,先访问第1层
(根),再访问第2层(根的左右孩子),接着第3层……逐层从左到右访问每个节点,直到所有节
点都被访问。所以对于这棵二叉树而言,我们可以简单的推论出这棵二叉树的层序遍历就是 : A B
C D NULL E F NULL NULL NULL NULL NULL NULL
2. 为什么要使用队列实现层序遍历二叉树?
用队列实现这棵二叉树的层序遍历,核心就是利用了队列“先进先出”的特性,刚好匹配层序遍历
“一层一层、从左到右”的需求。
3.怎样使用队列实现层序遍历二叉树呢?
利用队列实现二叉树层序遍历,核心是用队列存储节点和借助队列 “先进先出” 的特性,让二叉树
节点按 “一层一层、从左到右” 的顺序被访问,具体逻辑可拆解为 3 步:
1. 核心原理:队列如何适配层序需求
二叉树层序遍历要 “按层访问”,但二叉树节点靠指针( left / right )关联,本身无 “层” 的显式顺
序。队列的 “先进先出” 特性,能把二叉树的 “层次顺序” 转化为队列的 “线性顺序”:
- 处理当前层节点时,把下一层节点(左右子节点)按顺序入队 → 保证下一层节点会 “排队等
待”,按入队顺序被处理(契合层序 “从左到右、一层一层” 的规则)。
2. 队列的 “先进先出” 完美匹配层序遍历需求:
- “先进”:处理当前层节点时,优先把下一层的左子节点入队(保证层序 “从左到右”)。
- “先出”:队列头部始终是 “当前层最早入队的节点”,处理完弹出 → 保证层序 “一层一层” 推进。
对比其他结构(如栈):若用栈(后进先出),节点处理顺序会混乱,无法实现 “按层访问”。因
此,队列是层序遍历的 “最佳搭档”,用其特性弥补了二叉树层次顺序的隐式问题。
简单说,队列是层序遍历的 “工具”:用它的 “排队逻辑”,把二叉树的层次关系转化为可顺序处理的
线性结构,让层序遍历从抽象需求落地成代码逻辑 。
4. 代码的实现
层序遍历函数( levelOrder ):
void levelOrder(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头,出对头BTNode* top = QueueFront(&q);QueuePop(&q);printf("%c ", top->data);//将对头非空左右孩子入队列if (top->left){QueuePush(&q, top->left);}if (top->right){QueuePush(&q, top->right);}}QueueDestroy(&q);
}以下从层序遍历逻辑和队列与二叉树的关系两方面详细讲解:
层序遍历核心是按“一层一层”的顺序访问二叉树节点,借助队列实现,步骤如下:
1. 初始化队列
Queue q;
QueueInit(&q);
QueuePush(&q, root); - 先创建队列 q 并初始化,再把二叉树根节点 root 入队。此时队列里只有根节点,是层序遍历的
起点。
2. 循环处理队列(核心逻辑)
while (!QueueEmpty(&q))
{BTNode* top = QueueFront(&q); // 取队头(当前层节点)QueuePop(&q); // 弹出队头(处理完当前节点,出队)printf("%c ", top->data); // 访问节点数据(打印,也可做其他操作)// 非空左右孩子入队(为下一层遍历做准备)if (top->left) QueuePush(&q, top->left); if (top->right) QueuePush(&q, top->right);
}
- 循环条件:队列非空时,持续处理节点(队列空说明所有层遍历完毕)。
- 取节点 & 出队: QueueFront 拿到当前层的节点(队头), QueuePop 把它移出队列(因为要
处理该节点的逻辑了)。
- 访问节点:通过 top->data 访问当前节点数据(比如打印)。
- 子节点入队:若当前节点的左、右孩子非空,依次入队——这是层序遍历的关键!保证下一层节
点按顺序排队,后续循环会按“先入先出”处理,自然实现“一层一层”遍历。
3. 队列与二叉树的关系
层序遍历中,队列是“桥梁”,用“先入先出”特性适配二叉树“一层一层访问”的需求,具体关系体现
在:
1. 队列的作用:“暂存 + 顺序控制”
- 暂存节点:遍历某一层时,把当前层节点的非空左右孩子入队,这些孩子属于“下一层节点”。
- 顺序控制:队列保证节点“先进先出”,契合层序遍历“从左到右、一层一层”的顺序。比如根节点先
入队,处理根节点时,左、右孩子入队;后续先处理左孩子(队头),再处理右孩子(队列里排队
的),完美匹配层序遍历逻辑。
2. 二叉树结构对队列的依赖
二叉树节点是“分散”的(通过指针关联左右孩子),无法直接按“层”遍历。队列通过“入队(记录
下一层节点)→ 出队(处理当前层节点)”的流程,把二叉树“分层”的逻辑,转化为队列的“线性顺
序”操作,让层序遍历可实现。
4. 总结:
层序遍历函数用队列实现“分层访问”,队列的“先入先出”特性,完美匹配二叉树“一层一层遍历”的需
求:
- 队列暂存“下一层节点”,保证遍历顺序;
- 二叉树的“分层逻辑”,通过队列转化为简单的“入队 → 出队 → 处理”流程
4. 函数中用到的队列相关函数及其作用
假设队列的底层实现为“链式队列”,以下是各函数的功能说明:
1. QueueInit(&q)
- 作用:初始化队列 q ,通常包括设置队头/队尾指针为 NULL 、初始化节点数量等,确保队列可
正常使用。
2. QueuePush(&q, root)
- 作用:将节点 root 插入队列尾部(入队操作),保持“先进先出”的顺序。
- 层序遍历中,用于将当前节点的左右子节点加入队列,作为下一层的待处理节点。
3. QueueEmpty(&q)
- 作用:判断队列是否为空(返回 true 或 false )。
- 作为循环终止条件:当队列为空时,说明所有节点已遍历完毕。
4. QueueFront(&q)
- 作用:获取队列的队头节点(不删除节点),返回节点指针。
- 层序遍历中,用于获取当前层的待访问节点。
5. QueuePop(&q)
- 作用:删除队列的队头节点(出队操作)。
- 层序遍历中,处理完队头节点后将其移除,避免重复访问。
6. QueueDestroy(&q)
- 作用:销毁队列,释放队列占用的所有内存(包括所有节点)。
- 必须在遍历结束后调用(原代码放在循环内是错误的,会导致第一次循环后队列被销毁,后续操
作失败)。
注意 : 上面关于队列的函数小编均在之前的文章中都有讲过。想深入了解的小伙伴可以去看一看。
并且上面的代码都是基于队列和二叉树的代码基础上实现。
5. 总结:
levelOrder 函数通过队列实现二叉树层序遍历,核心总结如下:
1. 初始化队列并将根节点入队,作为遍历起点;
2. 循环处理队列(队列非空时):
- 取出队头节点,访问其数据(打印);
- 将该节点的非空左右子节点依次入队(为下一层遍历做准备);
3. 遍历结束后销毁队列
简言之,队列的“先进先出”特性保证了节点按“一层一层、从左到右”的顺序被访问,是层序遍历的
关键工具。
以上便是关于队列实现层序遍历二叉树的全部内容。最后感谢大家的观看!
