当前位置：首页 > news >正文

【模型剪枝1】结构化剪枝论文学习笔记

news 2025/7/26 11:24:49

一、背景

工作当中用到的模型不少，也遇到过对实时性要求比较高的场景，尽管对模型量化之后部署到边缘设备上，借助 NPU 实现推理加速的方式基本满足需求，但 Rockchip 官方支持量化的模型相对还是较少，如果使用模型库之外的模型可能就需要自己写量化过程，实现起来比较困难，一定程度上限制了模型选择。模型剪枝作为一种模型加速的方法，使用范围也很广泛，而且能够跟微调过程结合进行多次迭代优化，优化过程更加可控友好。最近有时间来学习一下模型剪枝，本文主要记录一下学习的几篇剪枝论文。这里介绍的几种剪枝方法都属于结构化剪枝，根据不同的评价标准确定不重要的卷积层，对这些不重要的卷积层剪枝。

二、L1-Norm based Filter Pruner

Paper： Pruning Filters for Efficient ConvNets

1. 核心思想

对网络中耦合层之间的 filters 计算重要性分数，对分数前 $m$ 小的 filters 进行剪枝，这些 filters 对应输出的特征图也会被移除，同时，以该特征图作为输入的下一层中对应位置的 filters 也会被相应剪枝。反映到网络结构上就是每个卷积层的输入输出通道被剪枝。

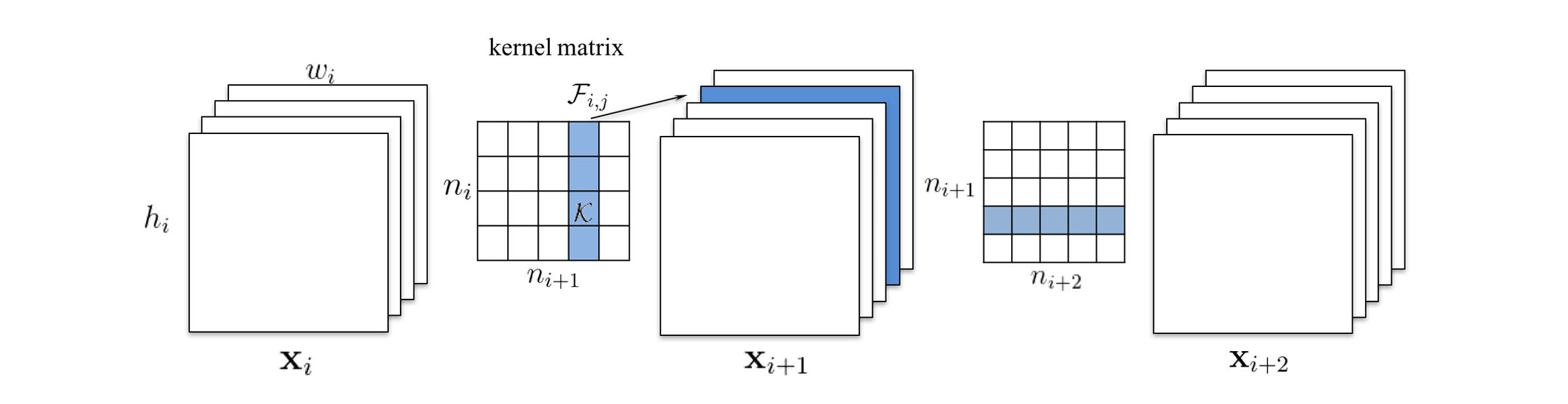
$\mathbf{x}_i\in \mathbb{R}^{n_i\times h_i\times w_i}$ ， $\mathbf{x}_{i+1}\in \mathbb{R}^{n_{i+1}\times h_{i+1}\times w_{i+1}}$ 分别表示第 $i$ 个卷积层的输入和输出特征图组， $\mathbf{x}_{i+1}$ 由 $n_{i+1}$ 个 3D filters $\mathcal{F}_{i,j}\in \mathbb{R}^{n_i\times k\times k}$ 与 $\mathbf{x}_i$ 卷积生成，而每一个 $\mathcal{F}_{i,j}$ 又是由 $n_i$ 个2D 卷积核 $\mathcal{K}\in \mathbb{R}^{k\times k}$ （这个就是通常所说的卷积核）组成的，所有 $n_i\times n_{i+1}$ 个 $\mathcal{K}$ 拼在一块，就是一个 4D 核矩阵（kernel matrix） $\mathcal{F}_i\in \mathbb{R}^{n_i\times n_{i+1}\times k\times k}$ 。 $\mathbf{x}_{i+1}$ 的第 $j$ 个特征图 $\mathbf{x}_{i+1,j}$ 由 $\mathcal{F}_i$ 中的第 $j$ 个 3D filter $\mathcal{F}_{i,j}$ 与 $\mathbf{x}_i$ 卷积生成。

2. 基本剪枝策略

首先剪枝的基本单位是 $\mathcal{F}_{i,j}$ ，重要性分数 $s_j$ 就是 $\mathcal{F}_{i,j}$ 的 L1 范数 $\left \| \mathcal{F}_{i,j}\right \|_1$ ， $s_j$ 的大小代表输出特征图的重要程度，我们剪掉的就是本层这些得分低的 $\mathcal{F}_{i,j}$ 及其对应生成的特征图，以及下一层对应的 filter（上图中第二个 kernel matrix 的蓝色部分）。

对每一个 filter，计算其权重绝对值 $s_j=\sum_{l=1}^{n_i}\sum_{}^{}\left | \mathcal{K}_l \right |$ ；
根据 $s_j$ 对 filters 排序；
剪掉前 $m$ 个 filters 及其对应的特征图，下一个卷积层中与剪掉的特征图对应的 filter 一并剪掉；
生成新的第 $i$ 层和 $i+1$ 层的 kernel matrix，把余下的权重复制到新模型中。

该剪枝方法与权重剪枝类似，权重剪枝属于非结构化剪枝，其剪枝的最小单位是卷积核中的每一个权重值，当权重低于某个阈值会被置 0，这样就会导致产生稀疏的卷积核，而稀疏矩阵的运算对大部分计算库来说是不友好的，也就很难被通用硬件加速。

3. 多层跨层剪枝策略

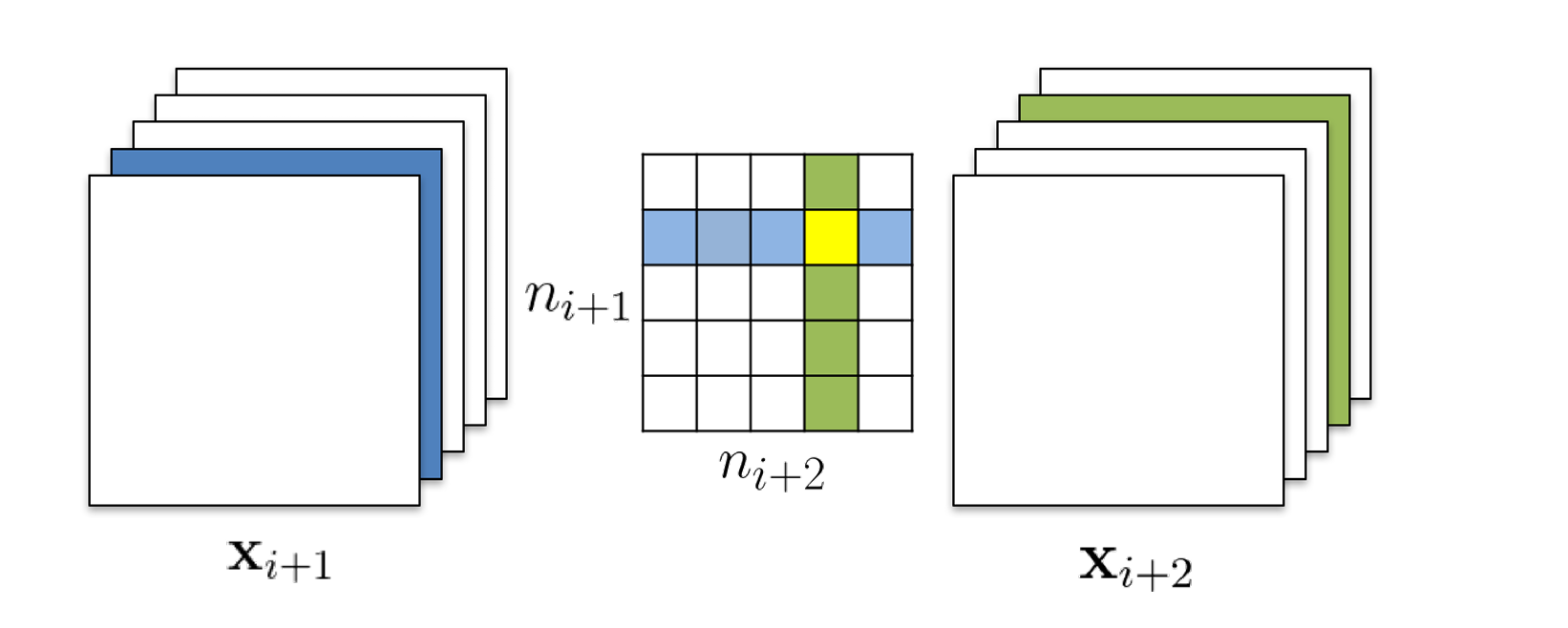
对于跨层和复杂层间连接的网络结构，考虑两种剪枝策略：

独立剪枝：重要性分数的计算只考虑当前层，与其他层无关。在上图中，剪枝 kernel matrix 的绿色区域的 filter 时， $s_j$ 的计算以绿色区域每个卷积核的原始权重的计算结果为准，所以黄色区域表示的卷积核仍为原始权重。
贪心剪枝：重要性分数的计算考虑之前层中被剪枝过的 filter。同样是剪枝绿色区域的filter，黄色区域的卷积核包含在上一层被剪掉的 filter 中，在计算 $s_j$ 时该卷积核就不再参与计算（全0）了。

两种策略生成的 kernel matrix 形状是相同的，不过是计算方式不同。作者指出虽然贪心剪枝策略不是全局最优，但剪枝后的模型往往精度更高。

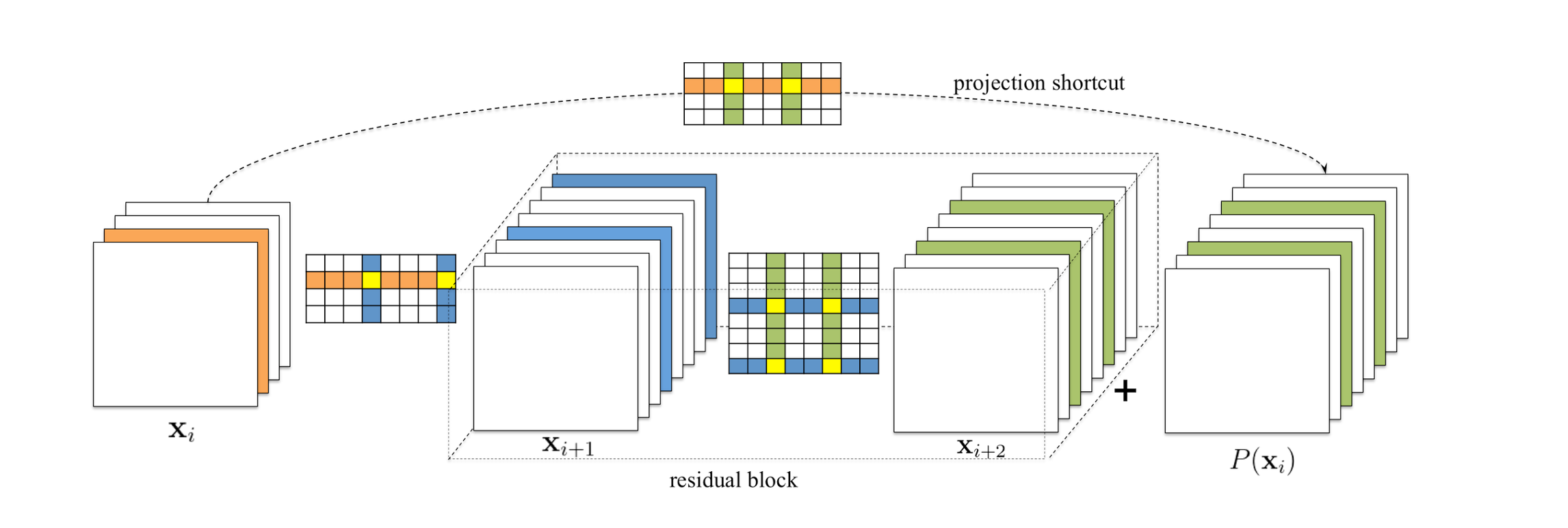
对于 ResNet 中的跨层直连结构，作者指出 identical 特征图 $P(\mathbf{x}_i)$ 比残差块的输出特征图 $\mathbf{x}_{i+2}$ 更重要，所以要先剪 $P(\mathbf{x}_i)$ ，再根据 $P(\mathbf{x}_i)$ 的结果定位 $\mathbf{x}_{i+2}$ 中相同位置的特征图，反推这些特征图对应的需要被剪枝的 filters。

4. 精度恢复

两种策略：

一次性剪枝并 retrain，直到精度恢复；
剪枝和 retrain 迭代，当前层剪完，retrain，再剪下一层，retrain，……，精度恢复。

作者指出，如果对敏感层中的 filters 进行剪枝，或者做大比例剪枝，精度恢复会很难，迭代剪枝的结果可能会更好，但是需要更多的 epochs。对于非敏感层使用一次性剪枝即可，精度恢复需要的时间也更短。

三、Network Slimming

Paper：Learning Efficient Convolutional Networks through Network Slimming

1. 核心思想

对 BN 层的缩放因子 $\gamma$ 施加 L1 正则约束，在训练过程中利用 L1 正则的稀疏性会产生很多近 0 的 $\gamma$ ，而每一个 $\gamma$ 又对应一个卷积通道，所以就可以用 $\gamma$ 的大小表示卷积通道的重要性，对不重要的卷积通道进行剪枝。

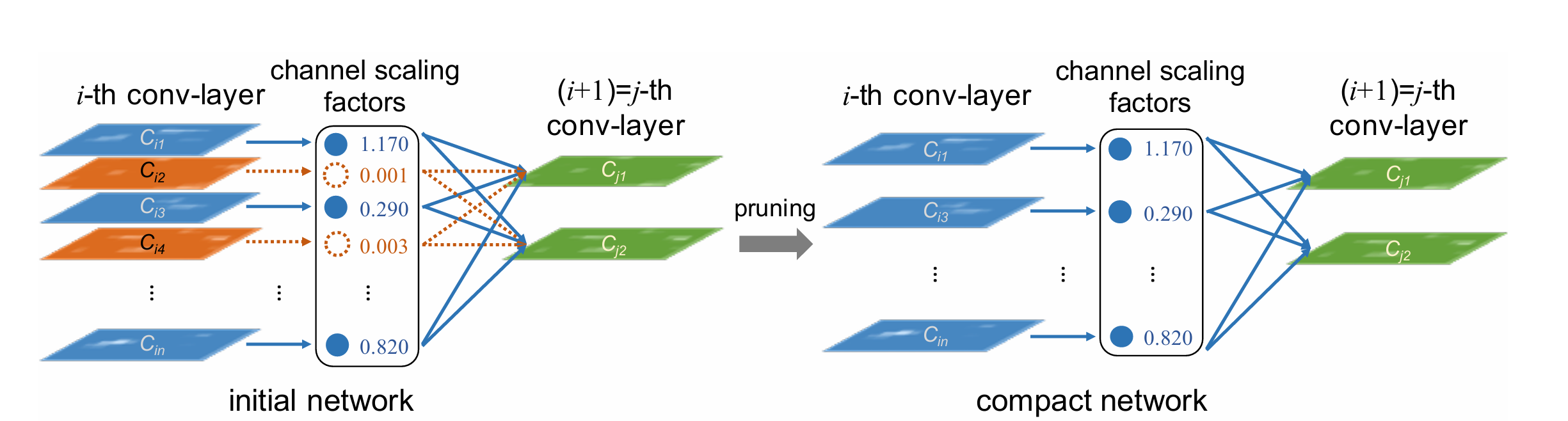
施加 L1 正则的训练过程称为稀疏化训练，稀疏化训练之后会标识各个卷积通道的重要性。

2. 通道剪枝的优势

权重剪枝属于细粒度剪枝，有高灵活性和高压缩比，但需要特定的硬件加速实现快速推理，层剪枝属于粗粒度剪枝，模型加速容易实现，但灵活性不够高，且只对深层网络（＞50层）加速效果明显；通道剪枝介于二者之间，够灵活而且易于实现，适用于任何类型的 CNN 或 FCN。

3. 稀疏化训练

整体目标函数：

$L=\sum_{(x,y)}^{}l((x,W),y)+\lambda \sum_{\gamma \in \Gamma }^{}g(\gamma )$

其中 $l(\cdot )$ 是 CNN 原本的损失函数， $g(\cdot )$ 是施加在缩放因子上的惩罚项，文中使用的是 L1 正则，即 $g(s)=\left | s \right |$ ， $\lambda$ 是平衡因子。而 $\gamma$ 选取的正是 BN 层中的 $\gamma$ ，没有加任何新参数，物尽其用。

$\hat{z}=\frac{z_{in}-\mu _{\mathcal{B}}}{\sqrt{\sigma _{\mathcal{B}}^{2}}+\epsilon }; z_{out}=\gamma \hat{z}+\beta$

作者说明了这样做的原因：

如果加入一个缩放层而不使用BN层，那么缩放层的值对于评估通道重要性没有意义，因为二者之间是单纯的线性关系；
BN层之前插入，缩放层的效果会被BN层的归一化过程替代；
BN层之后插入，对每个通道来说会有两个缩放因子，权重会连续经历两次缩放。

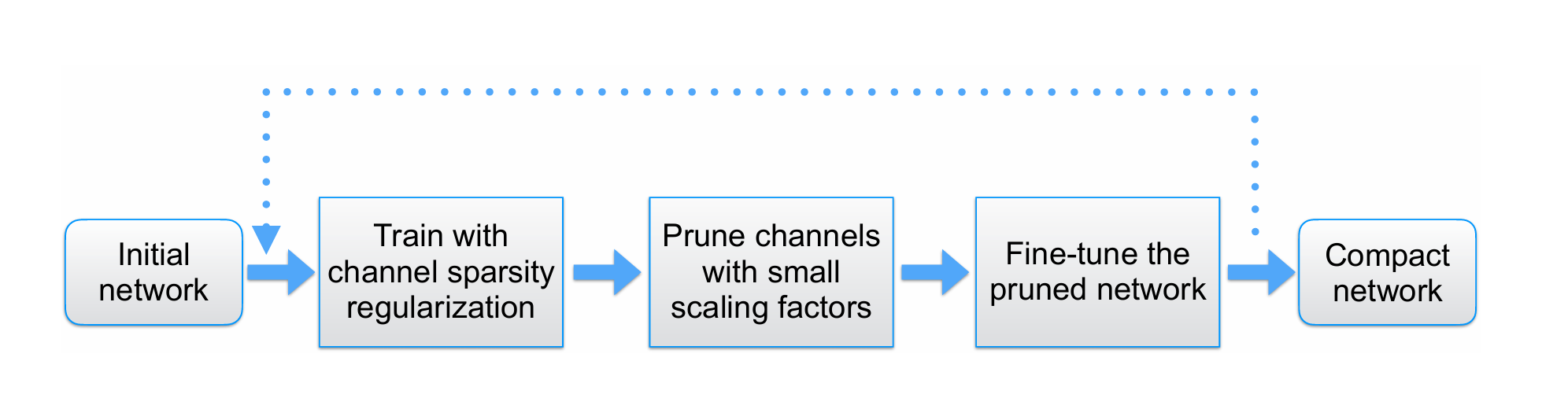
4. 剪枝微调

稀疏化训练完成后，就可以设置剪枝率 $r$ 和全局阈值来剪枝模型了。其中阈值的选取与 $r$ 有关，假设 $r=0.7$ ，我们首先对所有 BN 层的缩放因子的绝对值按升序排序，然后将 70% 位置处的 $\gamma$ 值作为全局阈值。剪枝之后若出现精度损失可以通过微调恢复。

除了上述这种单次剪枝，还可以进行多次循环剪枝，一次剪枝微调完成后再次剪枝，再次微调，反复进行，模型会越来越紧致，甚至精度还会有提升。

5. Channel Selection Layer

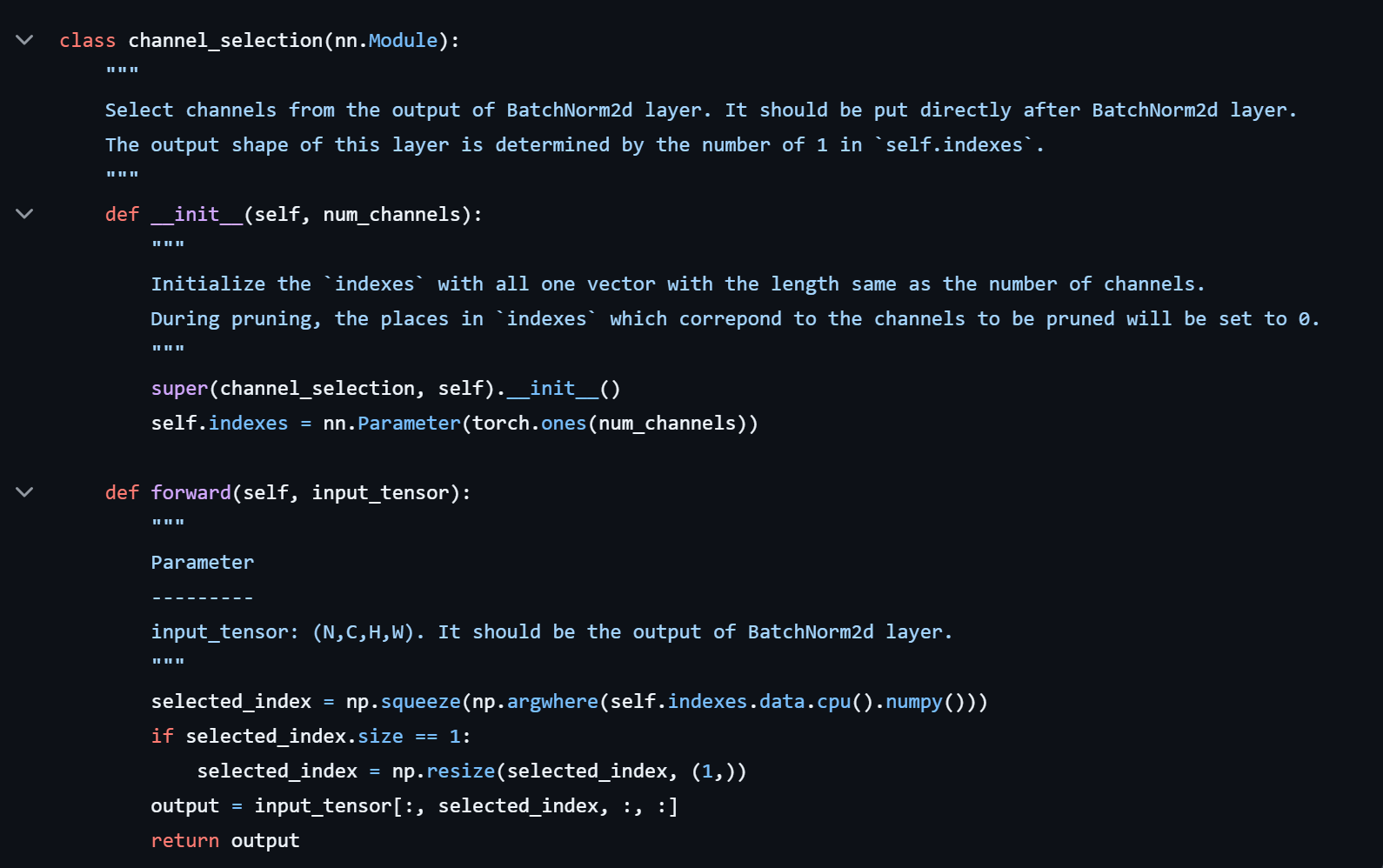
对于跨层连接和预激活单元（ResNet，DenseNet）这样的结构，当前层的输入会接收前面多个层的输出，且 BN 层在 Conv 层之前，这种情况下的稀疏操作在层的输入末端实现，实际输入通道数为其接收的所有通道的子集。具体实现上，是在BN层之后插入一个通道选择层 (channel selection layer)，该层有一个参数 indexes，用来存储通道索引，该参数在训练过程中不参与梯度更新，仅在剪枝时标识被剪枝通道的索引位置（置0），该层最终输出的就是没有被剪枝的通道，也即输入通道的一个子集。

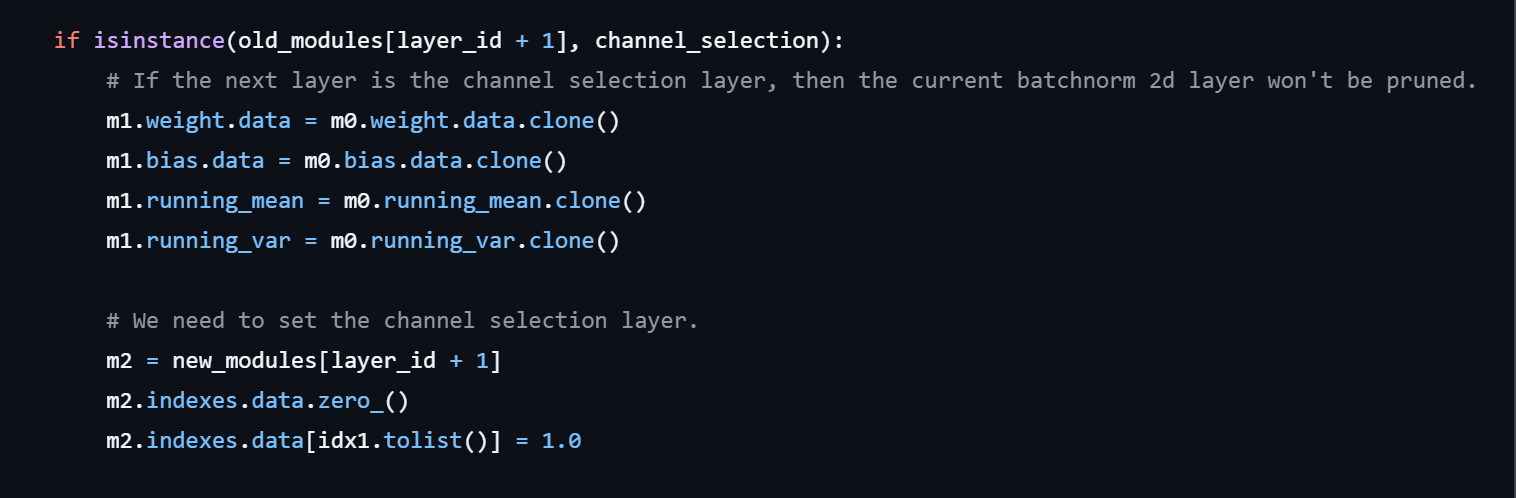
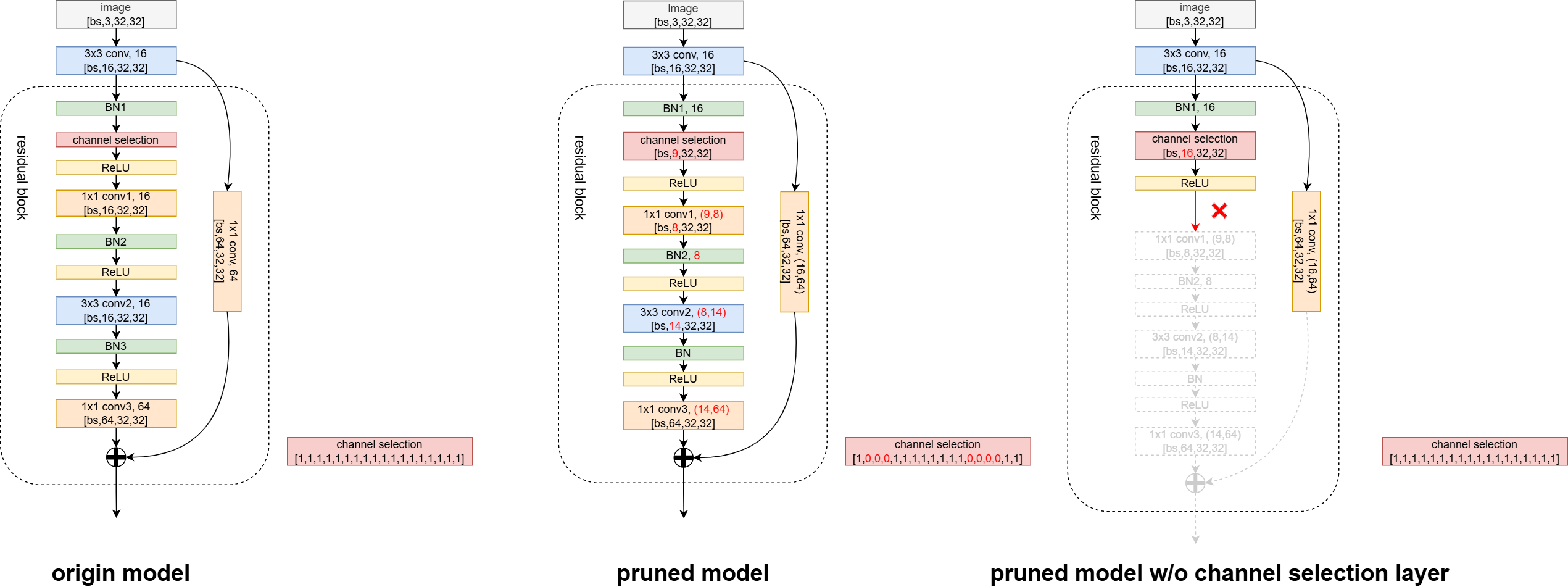
如果不使用 channel selection layer（相当于对 indexes 全部置 1），则 BN-Conv 这样的结构中的 BN 层不会被剪枝，BN 层输出的 channel 数不变，这样与后面剪枝的 Conv 层的输入通道数不匹配，无法计算。（仅个人理解）

四、Torch Pruning

Paper：[2301.12900] DepGraph: Towards Any Structural Pruning

1. 核心思想

设计了一种非深度图算法 DepGraph，能够自动分析模型内部各个层之间的耦合关系，剪枝时能够将具有依赖关系的参数一并剪掉。Torch Pruning 是基于该算法开发的一套剪枝框架，不仅其内部实现了很多剪枝器，用户还可以根据不同的剪枝算法自定义剪枝器。该方法最强大的地方在于，这是一种通用剪枝方法，支持的模型非常多，不仅是常见的各种视觉模型，还支持像Deepseek，Qwen，Llama 这样的大语言模型。

2. 依赖图

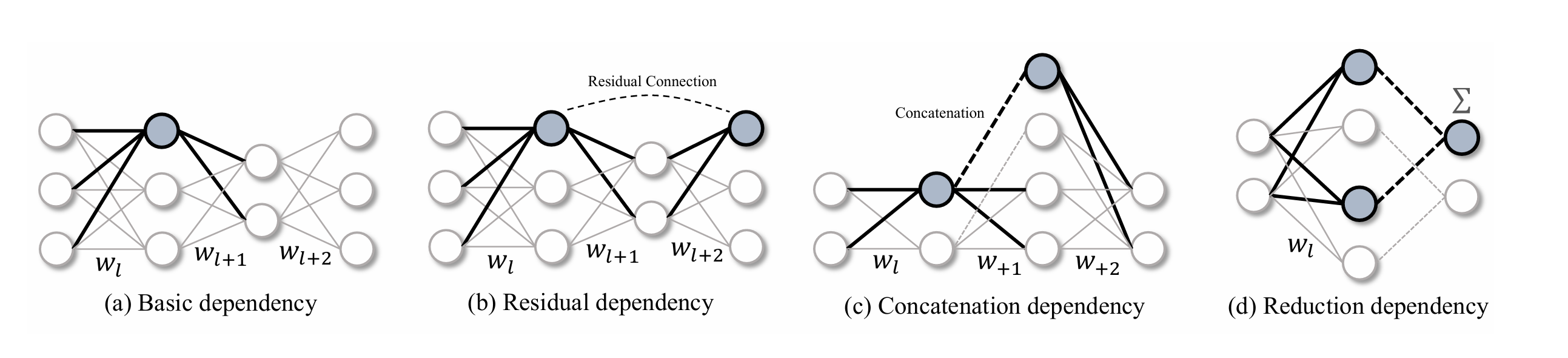
作者列举了网络中一些常见的依赖结构，对这些结构来说，某个神经元的移除必然会导致与该神经元有依赖关系的其它神经元的移除。但实际中不同模型中的依赖结构是千变万化的，我们不可能一一设计剪枝策略来应对这些结构。于是，一种通用且自动化的结构分析工具——依赖图（Dependency Graphy）被提了出来。

2.1 分组

首先定义一个分组矩阵 $G\in R^{L\times L}$ （ $L$ = 模型层数）， $G_{ij}=1$ 表示第 $i$ 层和第 $j$ 层之间存在依赖关系，当 $i=j$ 时 $G_{ij}=1$ ， $g(i)=\{j|G_{ij}=1\}$ 表示与第 $i$ 层存在依赖关系的其它层的集合。很明显 $G_{ij}$ 不仅与第 $i$ 层和第 $j$ 层相关，还与二者之间的中间层相关。我们的目标就是为每个模型找到一个 $G$ 。但实际上这个 $G$ 通常会非常庞大且复杂，很难直接估计。所以我们绕开 $G$ ，去估计一个 $G$ 的推导形式——依赖图 $D$ 。

2.2 依赖图

假设一个权重分组 $g=\{w_1,w_2,w_3\}$ ，其中三者之间存在如下依赖关系： $w_1\Leftrightarrow w_2$ ， $w_2\Leftrightarrow w_3$ ， $w_1\Leftrightarrow w_3$ ，很明显， $w_1$ 和 $w_3$ 之间的依赖关系可以由前两个依赖关系推出来， $w_1\Leftrightarrow w_3$ 就可视为冗余依赖。将上述过程推广到整个分组矩阵 $G$ ，则 $G$ 中必然存在大量冗余依赖，于是可以对 $G$ 尽心压缩，删除其中的冗余依赖，得到一个关于 $G$ 的更加紧致的表示。

定义一个依赖图 $D$ （可视作 $G$ 的 transitive reduction），只存储具有直接连接关系的层依赖。对于所有的 $G_{ij}=1$ ， $D$ 中都有一条对应的边 $e_{ij}$ 。

2.3 网络分解

然而在实际应用中会发现，同一个卷积层可能存在两种不同的剪枝方式，输入通道剪枝和输出通道剪枝，此外还有一些如跳跃连接的非参数化操作，这都不利于从层级别构建依赖图。于是作者进一步地对一个网络表示 $\mathcal{F}(x;w)$ 做了更细粒度的分解，作为层的集合表示为 $\mathcal{F}=\{f_1,f_2,...,f_L\}$ ，将每一层 $f_i$ 分解为输入 $f_i^{-}$ 和输出 $f^{+}_i$ ，转换为对层的输入和输出之间的依赖关系进行建模，所以网络的最终表示形式为 $\mathcal{F}=\left \{ f^{-}_1,f^{+}_1,f^{-}_2,f^{+}_2,...,f^{-}_L,f^{+}_L \right \}$ 。

2.4 依赖建模

基于上述分析，一个网络中包含两种主要的依赖关系：层间依赖和层内依赖。

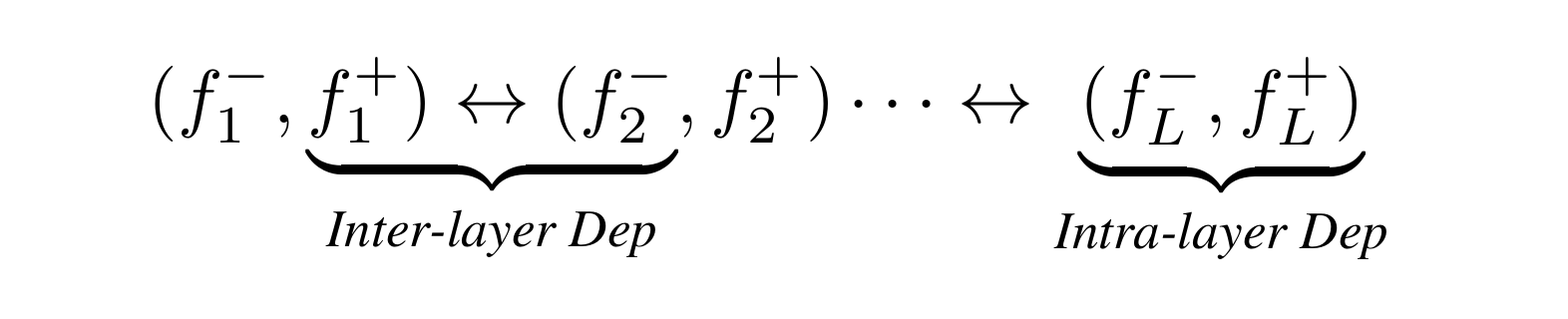
其中 $\leftrightarrow$ 表示两层相连。

层间依赖（inter-layer dependency）：如果前层输入与后层输出相连，则二者之间存在依赖关系，即 $f^{-}_i\leftrightarrow f^{+}_j\Rightarrow f^{-}_i\Leftrightarrow f^{+}_j$ ；
层内依赖（intra-layer dependency）：如果某层的输出和输出之间的剪枝策略相同（表示为 $sch(f^{-}_i)=sch(f^{+}_i)$ ），则二者之间存在依赖关系，即 $f^{-}_i\leftrightarrow f^{+}_i\Rightarrow f^{-}_i\Leftrightarrow f^{+}_i$ 。

层间依赖好理解，两个层相连会共享中间特征图，要剪肯定都剪，只剪一个特征图就断流了。对于层内依赖，如果满足 $sch(f^{-}_i)=sch(f^{+}_i)$ ，则输入和输出要同时剪，比如 BN 层；如果 $sch(f^{-}_i)\neq sch(f^{+}_i)$ ，则只剪其中一个，比如 Conv 层，因为 $w[:,k,:,:]\neq w[k, :, :, :]$ 。于是 $D$ 中的依赖关系可表示如下：

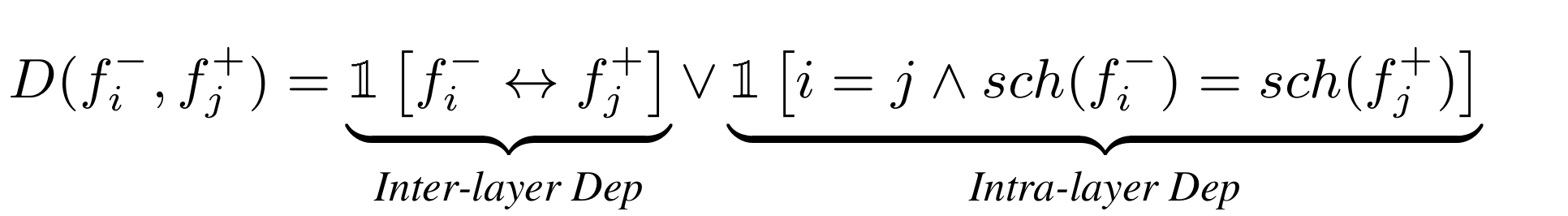
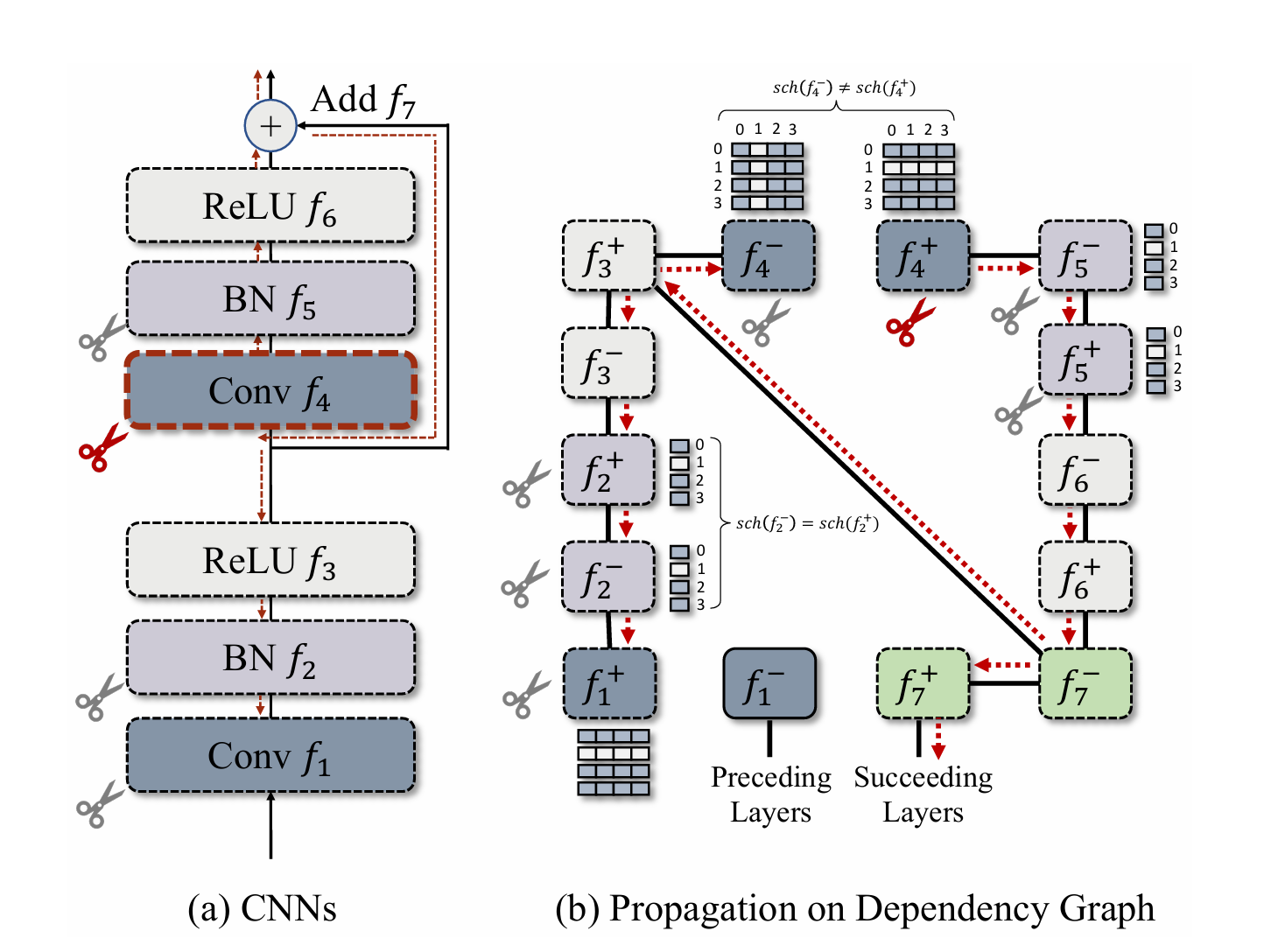
上图展示了一个依赖图的剪枝过程：首先从 $f_4$ 的输出通道 $f^{+}_4$ 开始剪枝，从 $f^{+}_4$ 开始寻找邻接点， $f^{-}_5$ 与其存在层间连接，需要被剪枝，同时 $f_5$ 是 BN 层，满足 $sch(f^{-}_5)=sch(f^{+}_5)$ ，所以 $f^{+}_5$ 也需要剪枝，由于跳跃连接的存在，虽然 $sch(f^{-}_4)\neq sch(f^{+}_4)$ ，但是为了保证 Add 操作的通道一致， $f^{-}_4$ 也要剪枝，也就是 $f^{-}_4$ 和 $f^{+}_4$ 属于一个权重分组。 $f^{+}_4$ 逻辑上连接 $f^{+}_3$ ，而 $f^{+}_3$ 又连接 $f^{+}_2$ ， $f^{+}_2$ 与 $f^{-}_4$ 存在层间连接，需要剪枝，而 $f_2$ 又是 BN 层，满足层内连接且共享剪枝策略，因此 $f^{-}_2$ 需要剪枝， $f^{-}_2$ 与 $f^{+}_1$ 满足层间连接， $f^{+}_1$ 需要剪枝， $f^{+}_1$ 与 $f^{-}_1$ 属于层间连接且不共享剪枝策略， $f^{-}_1$ 不需要剪枝。（ $f_3,f_6,f_7$ 没有权重参数不需要剪枝）

3. 组级别剪枝

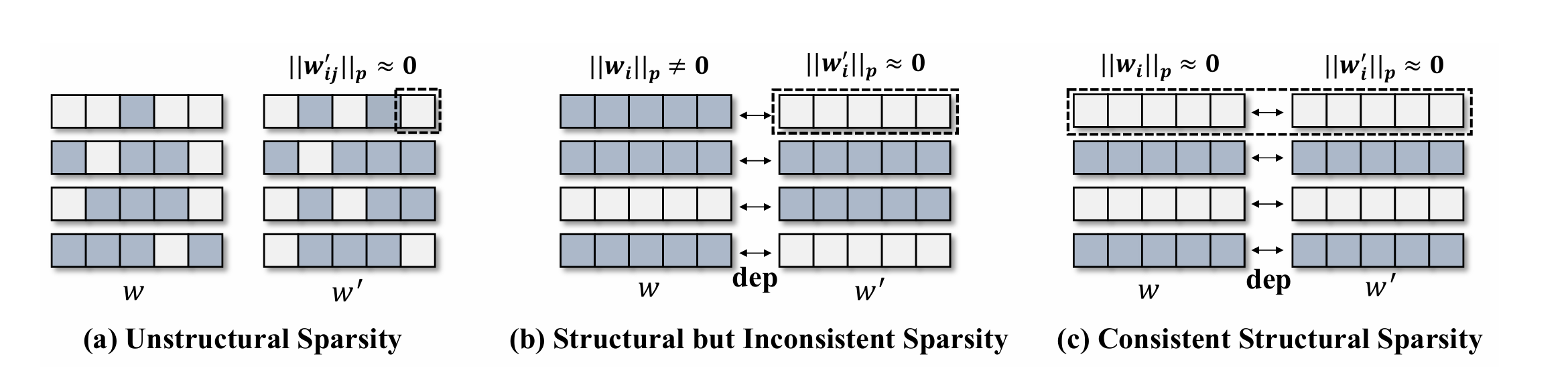
依赖图构建出来之后，就要根据依赖图进行剪枝了，那么剪枝标准该如何确定呢？作者首先考虑了基于 L2 范数的重要性分数（跟第一篇论文中的方法类似），给定一个参数分组 $g=\left \{ w_1,w_2,...,w_{\left | g \right |} \right \}$ ，计算每个 $w$ 的 L2 范数 $I(w)=\left \| w \right \|_2$ ，最终的分组重要性分数 $I(g)=\sum_{w\in g}^{}I(w)$ ，但是不同层的 $I(w)$ 无法求和。于是作者提出一种稀疏化训练方法，通过在参数分组 $g$ 上施加 L2 正则实现参数稀疏化。

$\mathcal{R}(g,k)=\sum_{k=1}^{K}\gamma _{k}\cdot I_{g,k}=\sum_{k=1}^{K}\sum_{w\in g}\gamma _k \left \| w[k] \right \|^{2}_2$

$\gamma _k=2^{\alpha \left ( I^{max}_g - I_{g,k} \right )/\left ( I^{max}_g - I^{min}_g \right )}$

其中 $I_{g,k}$ 表示参数 $w$ 第 $k$ 个通道的重要性分数， $\gamma _k$ 是强度因子。

稀疏化训练后可以得到一致性稀疏通道（如上图c），使用一个相对分数 $\hat{I}_{g,k}=\frac{N\cdot I_{g,k}}{\sum \left \{ TopN(I_g) \right \}}$ 进行剪枝。

五、总结

模型剪枝算是接触不久的一个方向，目前只是学了一点皮毛，读论文的过程中有些概念理解起来也比较有难度，结合代码反复读了好几遍才算理解个大概，如果有理解不对的地方也请大佬指正。本文介绍的几种剪枝方法属于相对好理解好上手的方法，后面随着工作需要可能会再学习其它方法。原本计划是论文学习笔记和代码实测放在一篇文章，等写完笔记发现内容挺多，那就分开记录吧，这样阅读起来目的性也更明确，下篇文章着重记录一下不同剪枝方法的实际使用。