当前位置：首页 > news >正文

深度图像滤波

news 2025/7/25 12:50:06

深度图像滤波是三维计算机视觉中的核心环节，旨在优化原始深度数据的质量，提升后续任务（如三维重建、物体识别、场景理解）的性能。本文讲解六种常见滤波：1.去噪滤波、2.边缘滤波、3.空域滤波、4.时域滤波、5.填洞滤波及6.各向异性滤波。

深度图像噪声特性与滤波需求

深度图像噪声来源

传感器物理噪声：
- TOF相机的飞行时间测量误差（通常为±10-50mm）
- 结构光系统的散斑噪声和相位解缠误差
- 双目视觉的匹配歧义与视差计算误差
环境干扰噪声：
- 强光环境下的背景光噪声（如户外阳光干扰）
- 反射表面（金属、玻璃）的多径效应
- 透明或半透明物体导致的错误深度值
几何噪声：
- 物体边缘的深度不连续性
- 遮挡区域导致的空洞边界噪声
- 低纹理区域的深度估计不确定性

深度滤波的核心目标

噪声抑制：降低随机噪声，提高深度测量的准确性
边缘保持：保留物体真实边界，避免过度平滑导致的几何失真
数据完整性：填充缺失区域，生成完整的深度图
时空一致性：在时间序列中保持深度值的稳定性，减少闪烁现象

在这里插入图片描述

一、去噪滤波：消除随机噪声

1.1 传统统计滤波器

均值滤波：
- 原理：用邻域像素的平均值替代当前像素值
- 公式： $Ifiltered(x,y)=1N∑(i,j)∈ΩI(i,j)I_{filtered}(x,y) = \frac{1}{N} \sum_{(i,j) \in \Omega} I(i,j)$
- 缺点：模糊边缘，不适用于深度图像
中值滤波：
- 原理：用邻域像素的中值替代当前像素值
- 优势：对椒盐噪声有效，能保留边缘
- 变种：自适应中值滤波（根据局部噪声水平调整窗口大小）
高斯滤波：
- 原理：基于高斯核的加权平均滤波
- 公式： $Ifiltered(x,y)=∑(i,j)∈ΩG(i,j)⋅I(i,j)I_{filtered}(x,y) = \sum_{(i,j) \in \Omega} G(i,j) \cdot I(i,j)$
- 特点：平滑效果随σ增大而增强，但会模糊边缘

1.2 基于模型的去噪方法

非局部均值滤波（Non-Local Means）：
- 原理：通过在整幅图像中寻找相似patch进行加权平均
- 公式： $Ifiltered(x)=∑y∈Ωw(x,y)⋅I(y)I_{filtered}(x) = \sum_{y \in \Omega} w(x,y) \cdot I(y)$
- 权重计算： $\frac{1}{Z(x)} \exp\left(-\frac{||N(x)-N(y)||^2}{h^2}\right)$
- 优势：能有效保留纹理细节，对高斯噪声效果显著
BM3D（Block-Matching 3D）：
- 原理：将相似patch分组为3D阵列，在变换域进行协同滤波
- 优势：当前最优的去噪算法之一，PSNR指标领先
- 局限性：计算复杂度高，实时性差

1.3 深度自适应去噪

深度域滤波：
- 原理：在深度值空间而非像素空间进行滤波
- 实现：将深度值映射到高维空间，在该空间进行聚类或平滑
- 优势：对深度跳跃区域有更好的适应性
基于法线的滤波：
- 原理：利用表面法线信息区分不同平面区域
- 步骤：
  1. 计算每个像素的表面法线
  2. 根据法线相似度构建邻域权重
  3. 基于权重进行加权平均
- 优势：能有效区分相邻平面，保留平面间的边缘

三、边缘滤波：保留几何边界

2.1 双边滤波（Bilateral Filter）

原理：同时考虑空间距离和像素值差异的加权滤波
$I_{\text{filtered}}(p) = \frac{\sum_{q \in \Omega} w(p,q) \cdot I(q)}{\sum_{q \in \Omega} w(p,q)}$

其中权重函数为：

$\exp\left(-\frac{||p-q||^2}{2\sigma_s^2}\right) \cdot \exp\left(-\frac{||I(p)-I(q)||^2}{2\sigma_r^2}\right)$

参数影响：
- σ_s：控制空间邻域大小，影响平滑范围
- σ_r：控制值域相似度阈值，影响边缘保留能力
优势：在平滑区域进行滤波，同时保留边缘信息
局限性：
- 对大的深度不连续区域效果有限
- 计算复杂度较高（O(N²)）

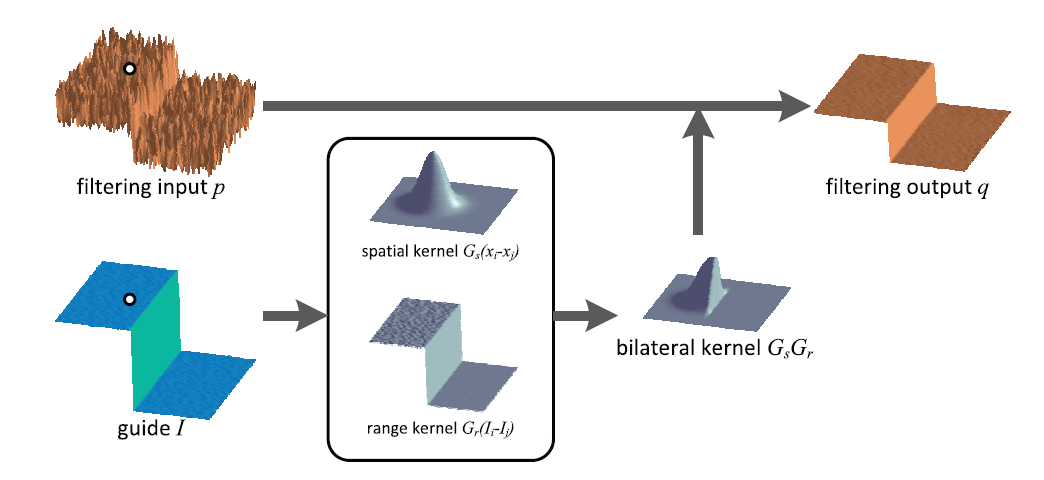
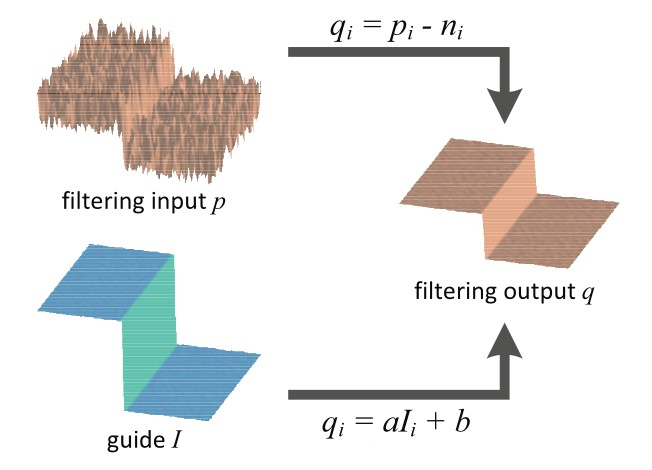
2.2 引导滤波（Guided Filter）

原理：利用引导图像（如RGB图像）的结构信息指导深度滤波
数学模型：假设输出与引导图像在局部窗口内呈线性关系

$q_i = a_k I_i + b_k, ∀i ∈ ω_k$

其中a_k和b_k通过最小化平方误差求得

优势：
- 边缘保留能力优于双边滤波
- 具有线性时间复杂度（O(N)）
- 可证明的边缘保持性和保真性
应用：常用于RGB-D相机的深度图优化（如Kinect Fusion）

2.3 边缘感知滤波网络（Deep Edge-Aware Filtering）

架构设计：
- 编码器-解码器结构提取多尺度特征
- 边缘检测分支显式预测深度边缘
- 注意力机制在边缘区域降低平滑强度
训练策略：
- 多任务损失：深度重建损失 + 边缘检测损失
- 对抗训练：引入判别器区分滤波结果与真实高质量深度图
优势：
- 能学习复杂场景下的边缘模式
- 对弱纹理区域的边缘有更好的保持能力

三、空域滤波：邻域信息融合

3.1 基于窗口的空域滤波

盒滤波（Box Filter）：
- 原理：用固定大小窗口内的平均值替代当前像素值
- 优势：计算高效（可通过积分图加速）
- 缺点：模糊边缘，不适用于深度图像
高斯窗口滤波：
- 原理：基于高斯核的加权平均，离中心越近权重越大
- 优势：平滑效果更自然，对噪声有更好的抑制能力
自适应窗口滤波：
- 原理：根据局部区域的方差或梯度动态调整窗口大小
- 实现：在平滑区域使用大窗口，在边缘区域使用小窗口
- 优势：平衡噪声抑制和边缘保持

3.2 基于图的空域滤波

超像素分割辅助滤波：
- 步骤：
  1. 将深度图像分割为超像素区域
  2. 在每个超像素内部进行一致性滤波
  3. 跨超像素边界进行边缘保持处理
- 优势：利用语义信息指导滤波，提高区域一致性
条件随机场（CRF）：
- 建模：将深度滤波视为能量最小化问题
  
  $E(D) = ∑_i ψ_u(D_i) + ∑_{i,j} ψ_p(D_i,D_j)$
- 一元项：数据项，惩罚与观测深度的偏差
- 二元项：平滑项，鼓励相邻像素深度相似但保留边缘
- 求解：图割（Graph Cuts）或信念传播（Belief Propagation）

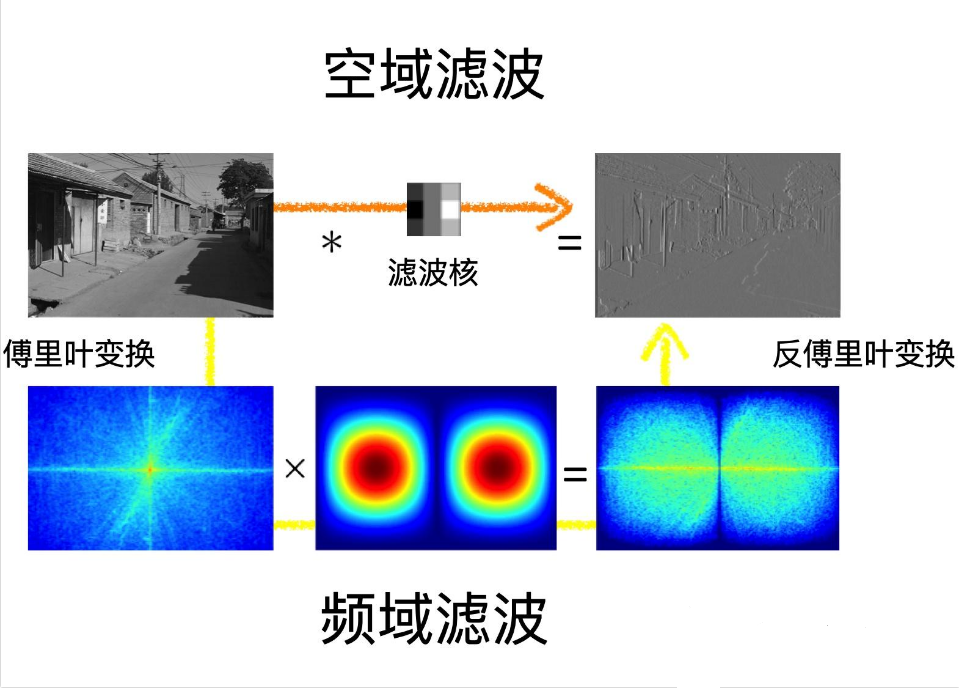
3.3 频域滤波方法

低通滤波：
- 原理：通过傅里叶变换将图像转换到频域，保留低频成分
- 应用：去除高频噪声
- 局限性：会模糊所有高频信息，包括边缘
带通滤波：
- 原理：保留特定频率范围的成分
- 应用：去除特定频率的周期性噪声（如结构光的条纹噪声）

在这里插入图片描述

四、时域滤波：时间序列平滑

4.1 帧间一致性滤波

移动平均滤波：
- 公式： $Dt=1N∑i=0N−1Dt−iD_t = \frac{1}{N} \sum_{i=0}^{N-1} D_{t-i}$
- 优势：简单有效，减少随机噪声
- 缺点：引入时间延迟，对快速运动物体不适用
指数加权移动平均（EWMA）：
- 公式： $D_t = αD_{t-1} + (1-α)D_{t}^{obs}$
- 参数：α∈[0,1]，控制历史帧权重
- 优势：对近期帧赋予更高权重，响应速度更快
- 变种：自适应EWMA（根据运动状态调整α）

4.2 卡尔曼滤波（Kalman Filter）

状态空间模型：
- 状态转移： $x_t = F_t x_{t-1} + w_t$
- 观测方程： $z_t = H_t x_t + v_t$
- 其中x_t为隐藏状态（深度值），z_t为观测值
递归估计步骤：
1. 预测：基于上一状态预测当前状态
2. 更新：结合当前观测值修正预测
优势：最优线性无偏估计，能处理动态系统
应用：机器人导航中的深度数据融合

4.3 光流辅助的时域滤波

原理：利用光流估计帧间对应关系，在对应区域进行滤波
实现步骤：
1. 计算相邻帧间的光流场
2. 根据光流将历史帧的深度值 warp 到当前帧
3. 在对应区域进行时空一致性滤波
优势：对动态场景有更好的适应性，减少运动模糊
局限性：光流计算误差会传播到深度滤波结果中

五、填洞滤波：修复缺失数据

5.1 基于传播的填洞方法

扩散方程法：
- 原理：基于热扩散方程，从空洞边缘向内部扩散有效深度值
- 数学模型： $∂D∂t=∇⋅(g(∣∇D∣)∇D)\frac{\partial D}{\partial t} = \nabla \cdot (g(|\nabla D|) \nabla D)$
- 其中g为扩散系数，在边缘处抑制扩散，在平滑区域促进扩散
快速行进法（Fast Marching Method）：
- 原理：基于Eikonal方程，从已知区域向未知区域推进
- 优势：保证最短路径传播，避免填充不合理的长距离路径
局限性：
- 对大空洞填充效果有限
- 无法恢复遮挡区域的真实深度

5.2 基于几何先验的填洞方法

平面拟合：
- 原理：假设空洞区域由局部平面组成，通过周围点拟合平面参数
- 应用：室内场景（墙面、地面等平面结构）
曲面插值：
- 方法：双三次插值、径向基函数插值等
- 优势：能拟合复杂曲面，但对非连续表面效果差
基于深度学习的几何先验：
- 预训练网络提取几何特征（如平面、圆柱体等）
- 利用几何约束指导空洞填充

5.3 基于RGB信息的深度补全

多模态融合方法：
1. 从RGB图像中提取语义和几何线索
2. 利用这些线索指导深度空洞填充
深度学习架构：
- 编码器-解码器结构处理RGB图像
- 跳跃连接融合RGB特征与深度特征
- 注意力机制关注边缘和语义边界
典型模型：
- DeepCompletion：结合RGB和稀疏深度生成密集深度图
- DenseDepth：基于单目RGB图像预测深度，用于辅助填洞

六、各向异性滤波：自适应平滑

6.1 各向异性扩散滤波

原理：基于热扩散方程，在梯度小的区域扩散快，梯度大的区域扩散慢
数学模型：

$\partial I / \partial t = d i v (g (∣\nabla I ∣) \nabla I) g (s) = e x p (- (s / K)^{2}) 或 g (s) = 1/ (1 + (s / K)^{2})$
参数影响：
- K：控制边缘敏感度，K越小越容易保留边缘
优势：自适应地平滑噪声，同时保护边缘
局限性：
- 参数选择敏感，需根据场景调整
- 迭代求解计算复杂度高

6.2 基于结构张量的各向异性滤波

原理：利用结构张量分析局部区域的主方向，沿主方向进行平滑
步骤：
1. 计算局部梯度
2. 构建结构张量 $J = ∇I∇I^T$
3. 特征分解获取主方向和次方向
4. 沿主方向进行更强的平滑
优势：对线性结构（如墙面、管道）有良好的保持效果
应用：工业检测中的表面缺陷检测

6.3 自适应各向异性滤波网络

架构设计：
- 特征提取模块分析局部结构
- 方向预测模块估计各向异性方向
- 滤波模块根据预测方向进行自适应平滑
训练策略：
- 使用合成数据（含噪声和已知地面真值）
- 对抗训练增强滤波结果的真实感
优势：能学习复杂场景下的各向异性模式，适应性更强

工程实践与评价指标

8.1 实时性优化策略

算法层面：
- 使用可分离卷积降低计算复杂度
- 设计轻量级网络架构（如MobileNet系列）
- 采用近似算法（如快速双边滤波）
硬件加速：
- GPU并行计算（如CUDA实现）
- FPGA/ASIC定制加速（适合特定算法）
- 边缘计算设备部署（如Jetson系列）

8.2 评价指标体系

定量指标：
- 均方误差（MSE）： $1N∑i=1N(Di−Digt)2\frac{1}{N} \sum_{i=1}^{N} (D_i - D_i^{gt})^2$
- 绝对相对误差（Abs Rel）： $1N∑i=1N∣Di−Digt∣Digt\frac{1}{N} \sum_{i=1}^{N} \frac{|D_i - D_i^{gt}|}{D_i^{gt}}$
- 阈值精度（Threshold Accuracy）：如δ<1.25的像素比例
- 边缘F1分数：边缘检测结果的精确率和召回率的调和平均
定性指标：
- 视觉质量：滤波后的深度图是否符合人类视觉感知
- 边缘保持度：物体边界是否清晰，有无过度平滑
- 空洞填充合理性：填充区域是否符合场景几何
- 动态稳定性：时间序列中深度值是否稳定