对粒子群算法的理解与实例详解
目录
一、概述
二、实例详解
1)问题说明
2)初始化参数
3)更新速度和位置
4)计算适应度值
5)更新最优解
6)迭代结束
三、总结
一、概述
在对粒子群算法进行讲解之前,首先谈谈智能优化算法的共同之处。前面已经介绍了遗传算法、蚁群算法的基本思想和实现思路,从中我们其实可以发现这些算法的共同之处。他们都是基于概率的搜索算法,首先初始化一组解,然后根据这组解的适应度,并结合概率的随机性来变化生成下一组解,所不同之处也只在于对新一组解的生成方式不同,这也是区分不同智能搜索算法的核心之处。
粒子群算法也是一种智能优化算法,它与其它优化算法一样具有上述特征。其解的优化改进模拟的正是鸟群或鱼群的社会行为。那鸟群的社会行为有什么特征呢?鸟群在觅食过程中,一群鸟在空中四处飞翔寻找食物源,不同的鸟通过共享信息来改变自己的飞行方向,从而最终使所有的鸟都能找到并汇集到最好的食物源。粒子群算法正是利用了鸟群共享信息这一特征,从而用于调整解的改进方式。
而对应到实际的算法中,粒子群算法具体是如何实现优化改进的呢,它利用了哪些信息呢?对应着鸟群来开,粒子群算法涉及到的主要信息有5个,包括:粒子、位置、速度、个体最优解和群体最优解。
粒子:就是问题解空间中的一个解,当然这不一定是最优解,群体由这些粒子组成。
位置:即粒子所在的位置,它的表示方式可以和粒子的表示方式一样,比如粒子是一个多维向量,则位置可以用这个多维向量代替。
速度:表示粒子移动的速度和方向,注意这是一个矢量,它表示了粒子移动的速度,也表示解变化的方向和快慢。
个体最优解:表示一个粒子在变化过程中所得到的最优的解。
群体最优解:表示群体中,所有个体的最优解。
基于上述5个核心信息元,粒子群算法的步骤如下:
-
初始化粒子群(随机位置和速度)
-
计算每个粒子的适应度值
-
更新个体最优位置(pbest)
-
更新全局最优位置(gbest)
-
更新粒子速度和位置
-
重复步骤2-5直到满足终止条件。
上述5个信息元素在每次迭代中均会重新计算,具体计算公式在实例详解中进行详细说明。
二、实例详解
1)问题说明
求解Schwefel函数最小值,Schwefel函数是一个经典的多峰测试函数,具有许多局部极小点,其全局最小值位于搜索空间的边界附近。它的一个典型形式如下:
f = 418.9829 * D- ∑(x .* sin(sqrt(abs(x))));其中D为向量x的维度。
2)初始化参数
针对此问题初始化粒子群算法参数如下。粒子群数量为40,函数变量维度取2(这与算法本身参数无关),最大迭代次数设置为200,初始惯性权重为0.9(表示粒子保持原有移动速度和方向的权重),初始个体学习因子2.5(表示粒子向自身最优解移动的权重),初始社会因子为2.5(表示粒子向当前全局最优解移动的权重)。然后是限定了粒子运动的范围和搜索的最大速度限定值。
初始粒子群体存放在数组particles中,它是一个结构体数组变量,每个particles代表一个粒子。而每个粒子又包含位置、速度、适应度值、最佳位置和最佳适应度值5个元素。在本程序中,位置、速度均是二维向量。如particles(i).position = x_min + (x_max - x_min) * rand(1, n_dims)随机生成了一个二维行向量。
n_particles = 40; % 粒子数量n_dims = 2; % 问题维度(可修改为2, 5, 10等)max_iter = 200; % 最大迭代次数% 自适应参数设置w_max = 0.9; % 初始惯性权重w_min = 0.4; % 最终惯性权重c1_max = 2.5; % 初始个体学习因子c1_min = 0.5; % 最终个体学习因子c2_max = 2.5; % 初始社会学习因子c2_min = 0.5; % 最终社会学习因子% Schwefel函数搜索范围x_min = -500;x_max = 500;v_max = (x_max - x_min) * 0.2; % 最大速度设为搜索范围的20%% 初始化粒子群particles = struct();for i = 1:n_particles% 随机初始化位置和速度particles(i).position = x_min + (x_max - x_min) * rand(1, n_dims);particles(i).velocity = -v_max + 2*v_max * rand(1, n_dims);particles(i).fitness = schwefel(particles(i).position);particles(i).pbest_position = particles(i).position;particles(i).pbest_fitness = particles(i).fitness;end% 初始化全局最优[gbest_fitness, idx] = min([particles.pbest_fitness]);gbest_position = particles(idx).pbest_position;3)更新速度和位置
速度更新公式如下图所示,式中,w是一个随机产生的系数,它反映的是当前速度对新的速度的贡献度,该系数也可以设置为一个固定值,也可根据需要随机产生。c由学习因子产生,r由随机产生。c1和r1反映粒子自身的最优解对新速度的贡献,c2和r2反映的是全局的最优解对新速度的贡献。
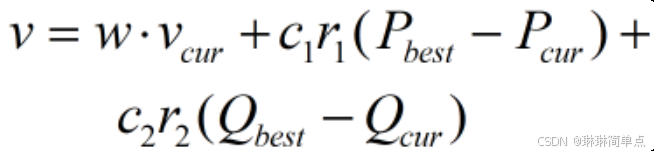
需要进一步说明的是,虽然此处名义上是更新速度,而实际上所做的工作就是计算当前粒子在进入下一步迭代时需要移动的位置量,该速度直接用于更新粒子的位置。正如下代码所示,具体代码实现中对速度和位置进行了范围限制,这个限制操作根据实际问题而定。
% 更新速度
r1 = rand(1, n_dims);
r2 = rand(1, n_dims);
particles(i).velocity = w * particles(i).velocity ...+ c1 * r1 .* (particles(i).pbest_position - particles(i).position) ...+ c2 * r2 .* (gbest_position - particles(i).position);% 速度边界限制
particles(i).velocity = max(particles(i).velocity, -v_max);
particles(i).velocity = min(particles(i).velocity, v_max);% 更新位置
particles(i).position = particles(i).position + particles(i).velocity;% 位置边界限制(反射边界处理)
over_min = particles(i).position < x_min;
over_max = particles(i).position > x_max;
particles(i).position(over_min) = 2*x_min - particles(i).position(over_min);
particles(i).position(over_max) = 2*x_max - particles(i).position(over_max);
particles(i).velocity(over_min | over_max) = -0.5 * particles(i).velocity(over_min | over_max);4)计算适应度值
在本问题中,我们直接以Schwefel函数作为适应度韩式,因此计算适应度值时只需要将更新后的粒子代入函数中即可。particles(i).fitness = schwefel(particles(i).position);
5)更新最优解
更新最优解的代码实现如下,需要注意的是,此处需要更新两类最优解,一个是单个粒子自身自开始迭代以来的最优解,第二个是整个粒子群的最优解。实现方式均很简单,利用适应度值比较,然后保留最优的即可。
% 更新个体最优if particles(i).fitness < particles(i).pbest_fitnessparticles(i).pbest_fitness = particles(i).fitness;particles(i).pbest_position = particles(i).position;% 更新全局最优if particles(i).fitness < gbest_fitnessgbest_fitness = particles(i).fitness;gbest_position = particles(i).position;endend6)迭代结束
粒子群算法迭代结束条件也很简单,可以是收敛精度,也可以是迭代步数结束。整个程序的实现可参见源代码。程序运行结果如下图所示,程序最终准确找到了最优解。
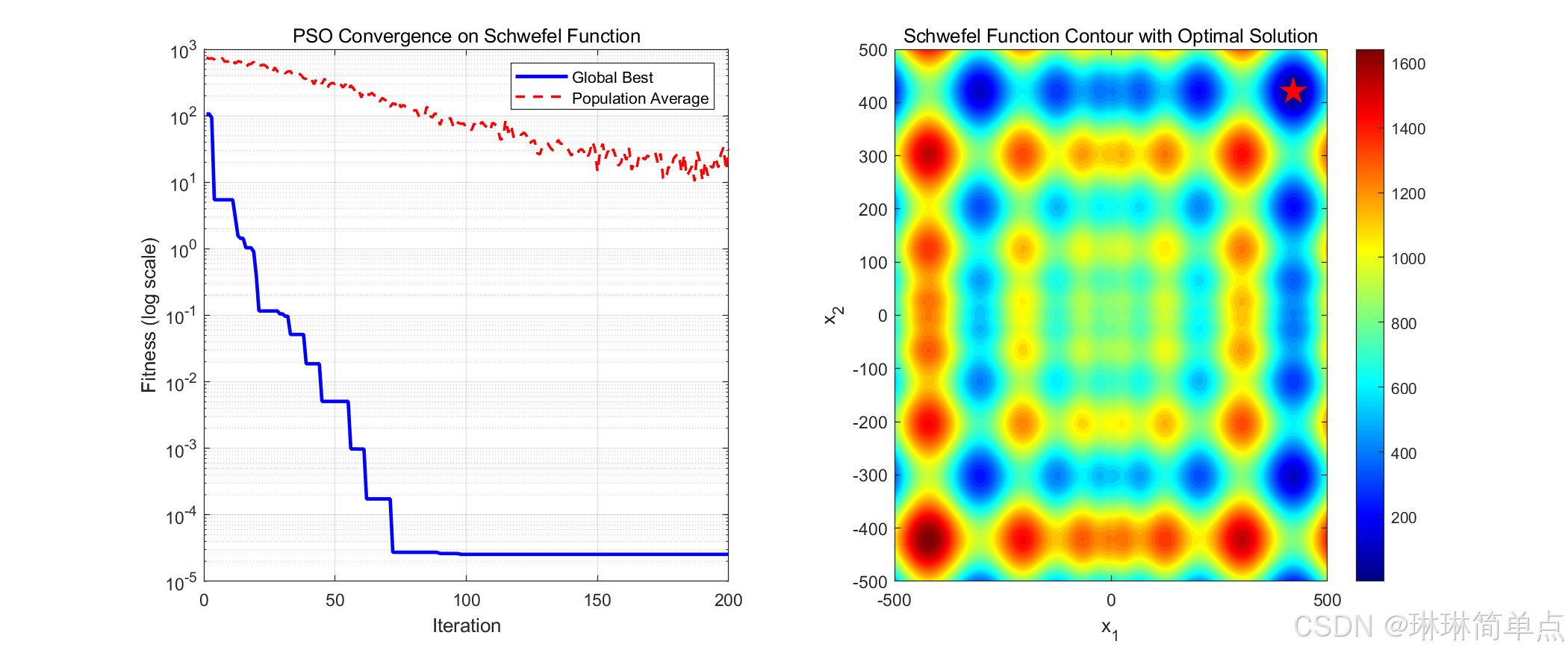
三、总结
相比其它智能优化算法,粒子群算法的思想更加简单易理解,其实现过程也相对更加简单。由于粒子群算法具有很好的全局搜索特性,能够较好避开局部最优解,因此,在多极值的问题中适合采用粒子群算法寻找最优解。但粒子群算法的计算量相对较大,占用资源较多。
