Order Capital Round 1 (Codeforces Round 1038, Div. 1 + Div. 2) C、D

C. Manhattan Pairs

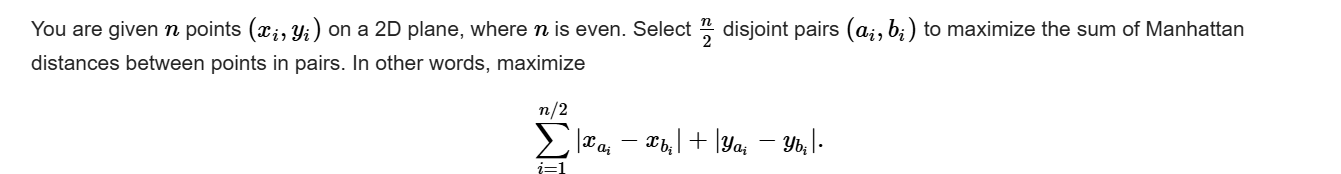
如果是一维的那就好办了，直接排序然后首尾元素相配对，直接贪心即可，但要注意这里是二维空间我们不妨将上述想法移用一下 A.左上 B.左下 C.右上 D.右下

于是就有

解方程有

可得正好配对的方案：先对x排序，再分别对前半段与后半段的y进行排序，再进行配对即可

Code：

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
struct node{int x, y,pos;
}a[N];
bool cmp1(node u,node v) {return u.x<v.x;
}
bool cmp2(node u,node v) {return u.y<v.y;
}
void solve() {int n;cin>>n;for(int i=1;i<=n;i++) {cin>>a[i].x>>a[i].y;a[i].pos=i;}sort(a+1,a+1+n,cmp1);sort(a+1,a+n/2+1,cmp2);sort(a+1+n/2,a+n+1,cmp2);for(int i=1;i<=n/2;i++) {cout<<a[i].pos<<" "<<a[n-i+1].pos<<endl;}
}
int main() {int T;cin>>T;while(T--) {solve();}return 0;
}

D. Traffic Lights

采用dp思路：dp[t,x],表示时间t时候到x点需要停留的最短时间，这里外层枚举时间内层更新转移dp即可

Code：

#include<bits/stdc++.h>
using namespace std;
void solve() {int n,m;cin>>n>>m;vector<vector<int>> adj(n);for(int i=1;i<=m;i++) {int x,y;cin>>x>>y;x--;y--;adj[x].push_back(y);adj[y].push_back(x);}vector<int> dp(n,0x3f3f3f3f);dp[0]=0;for(int t=0;t<2*n;t++) {vector<int> tmp(n,0x3f3f3f3f);for(int u=0;u<n;u++) {int v=adj[u][t%adj[u].size()];tmp[v]=min(tmp[v],dp[u]);tmp[u]=min(tmp[u],dp[u]+1);}dp=tmp;if(dp[n-1]!=0x3f3f3f3f) {cout<<t+1<<" "<<dp[n-1]<<endl;return;}}
}
int main() {int T;cin>>T;while(T--) {solve();}return 0;
}