当前位置：首页 > news >正文

离散与组合数学杂记

news 2025/7/18 13:23:00

生成函数

概念

又称母函数把一个无穷数列 ${a_n\}$ （默认从 $0$ 项起）表示成 $G(x)=∑i≥0aixiG(x)=\displaystyle\sum_{i\ge0} a_ix^i$ 的函数形式。例如：

$a_i=2^i$ ： $G(x)=∑i≥02ixiG(x)=\displaystyle\sum_{i\ge 0} 2^i x^i$ ；
$a_i=1$ ： $G(x)=∑i≥0xiG(x)=\displaystyle\sum _{i\ge 0} x^i$ 。

应用

用来帮助推导数列的通项公式（比如斐波那契数列）也可以作为条件形式以数列形式给出的象征。一个特别的转化：逆运用等比数列求和公式，可以得到： $11−ax=∑i≥0aixi\displaystyle\dfrac{1}{1-ax}=\sum_{i\ge0}a^ix^i$ ，等号左边不带求和符号部分的，称为生成函数的封闭形式。

生成函数的乘法运算有意义，其卷积形式是函数直接相乘。对于 $A(x)=∑i≥0aixiA(x)=\displaystyle\sum_{i\ge0}a_ix^i$ 和 $A(x)=∑i≥0bixiA(x)=\displaystyle\sum_{i\ge0}b_ix^i$ ：
$A×B=∑i≥0n(xi∑j=0iajbi−j)A\times B=\sum_{i\ge0}^n\left(x^i\sum_{j=0}^ia_jb_{i-j}\right)$

洛谷 P10780 BZOJ3028 食物

题意

题目传送门。

思路

根据上文，将这个背包问题转化为，考虑每一种物品拿的个数的生成函数，并用封闭形式表示：

偶数个形如 ${1,0,1,0,1,......\}$ ： $∑k≥0x2k=11−x2\displaystyle\sum_{k\ge 0} x^{2k}=\frac{1}{1-x^2}$ ；
$0$ 或 $1$ 个形如 ${1,1,0,0,0,......\}$ ： $1 + x$ ；
$0$ 或 $1$ 或 $2$ 个形如 ${1,1,1,0,0,......\}$ ： $1+x+x^2$ ；
奇数个形如 ${0,1,0,1,0,......\}$ ： $∑k≥0x2k+1=x∑k≥0x2k=x1−x2\displaystyle\sum_{k\ge 0}x^{2k+1}=x\displaystyle\sum_{k\ge 0} x^{2k}=\frac{x}{1-x^2}$ ；
$4$ 的倍数个类似第一条： $∑k≥0x4k=11−x4\displaystyle\sum_{k\ge 0}x^{4k}=\frac{1}{1-x^4}$ ；
$0$ 或 $1$ 或 $2$ 或 $3$ 个形如 ${1,1,1,0,0,......\}$ ： $1+x+x^2+x^3$ ；
$3$ 的倍数个类似第一条： $∑k≥0x3k=11−x3\displaystyle\sum_{k\ge 0}x^{3k}=\frac{1}{1-x^3}$ .

全部乘起来，并用二项式定理化简 $1+x+x^2$ 和 $1+x+x^2+x^3$ ：
$x(1−x)4\frac{x}{(1-x)^4}$

考虑推 $1(1−x)k=(11−x)k\dfrac{1}{(1-x)^k}=\left(\dfrac{1}{1-x}\right)^k$ 是哪个生成函数的封闭形式与该生成函数的第 $n$ 项系数，因为 $11−ax=∑i≥0aixi\displaystyle\dfrac{1}{1-ax}=\sum_{i\ge0}a^ix^i$ ， $a = 1$ 时， $11−x=1+x+x2+x3+...\dfrac{1}{1-x}=1+x+x^2+x^3+...$ 。 $k$ 次方展开后，相当于选 $k$ 个自然数和为 $n$ 的方案数：先给 $k$ 个数加 $1$ 转化问题为 $k$ 个正整数和为 $n + k$ ，运用插板法得知方案数为 $(n+k−1k−1)\dbinom{n+k-1}{k-1}$ 。

回到这一题 $1(1−x)4\frac{1}{(1-x)^4}$ 的第 $n - 1$ 项系数为 $(n−23)\dbinom{n-2}{3}$ ，乘回 $x$ 后即为答案。代码略。

Polya 计数

等我完全理解完再回来补。先给结论：用 $k$ 中颜色给 $n$ 个点的环染色方案数为 $1n∑i=0n−1kgcd⁡(n,i)\dfrac{1}{n}\displaystyle\sum_{i=0}^{n-1}k^{\gcd(n,i)}$ ，可否感性理解呢？

洛谷 P4980 【模板】Pólya 定理

题意

用 $n$ 种颜色给 $n$ 个点染色的方案数。两种方案相同，当且仅当一种方案能够旋转变为“另一方案”。

$n≤109n\le 10^9$ 。

思路

问题是如何快速算出 $1n∑i=0n−1ngcd⁡(n,i)\dfrac{1}{n}\displaystyle\sum_{i=0}^{n-1}n^{\gcd(n,i)}$ 。不妨暴力枚举 $n$ 的约数 $d=gcd⁡(n,i)d=\gcd(n,i)$ ，变为：
$1n∑d∣nndφ(nd)\dfrac{1}{n}\displaystyle\sum_{d|n}n^d\varphi(\frac{n}{d})$

$n$ 太大了不能预处理 $φ\varphi$ ，记得勤取模。时间复杂度为 $T(n)=∑i≥0{O(i)+O(n/i)}=O(n3/4)T(n)=\displaystyle\sum_{i\ge 0}\{O(\sqrt{i})+O(\sqrt{n/i})\}=O(n^{3/4})$ （根据主定理推得）。代码略。

第二类斯特林数

~~为什么先说第二类，因为第二类好像常用一些。~~

斯特林数将两个典型的模型的方案数求解变成一个类似组合数的东西。

概念

${nm}\begin{Bmatrix} n\\ m \end{Bmatrix}$ 表示，将 $n$ 个不同的球放进 $m$ 个相同的盒子里，且每个盒子都非空的方案数。

其递推式的推导：

球 $n$ 单开一个盒子，那么剩下 $n - 1$ 个球放进 $m - 1$ 个盒子： ${n−1m−1}\begin{Bmatrix} n-1\\ m-1 \end{Bmatrix}$ ；
球 $n$ 放进非空的 $m$ 个盒子： $m{n−1m}m\begin{Bmatrix} n-1\\ m \end{Bmatrix}$ 。

所以 ${nm}={n−1m−1}+m{n−1m}\begin{Bmatrix} n\\ m \end{Bmatrix}=\begin{Bmatrix} n-1\\ m-1 \end{Bmatrix}+m\begin{Bmatrix} n-1\\ m \end{Bmatrix}$ 。

特别的， ${n0}=[n=0]\begin{Bmatrix} n\\ 0 \end{Bmatrix}=[n=0]$ ，中括号表示艾弗森括号。

可以 $O(n^2)$ 预处理。

应用

先证明其通项公式，发现其满足下降幂性质：
在这里插入图片描述

CF932E Team Work

题意

给定 $n, k$ ，求 $∑i=1n(ni)ik\displaystyle\sum_{i=1}^n\dbinom{n}{i}i^k$ 。

$n≤109n\le 10^9$ ， $k≤5000k\le 5000$ 。

思路

把组合数用阶乘拆开，再运用斯特林数下降幂的性质：

$∑i=0nn!i!(n−i)!∑j=0k{kj}i!(i−j)!\sum_{i=0}^n\frac{n!}{i!(n-i)!}\sum_{j=0}^k\begin{Bmatrix} k\\ j \end{Bmatrix}\frac{i!}{(i-j)!}$

改变 $i$ 和 $j$ 的枚举顺序， $i$ 从 $j$ 开始到 $n$ ：
$∑j=0k{kj}∑i=jnn!(n−i)!(i−j)!\sum_{j=0}^k\begin{Bmatrix} k\\ j \end{Bmatrix}\sum_{i=j}^n\frac{n!}{(n-i)!(i-j)!}$

强制变成组合数：
$∑j=0k{kj}n!(n−j)!∑i=jn(n−j)!(n−i)!(i−j)!\sum_{j=0}^k\begin{Bmatrix} k\\ j \end{Bmatrix}\frac{n!}{(n-j)!}\sum_{i=j}^n\frac{(n-j)!}{(n-i)!(i-j)!}$

$∑j=0k{kj}n!(n−j)!∑i=jn(n−ji−j)\sum_{j=0}^k\begin{Bmatrix} k\\ j \end{Bmatrix}\frac{n!}{(n-j)!}\sum_{i=j}^n\binom{n-j}{i-j}$

化成 $2$ 次幂形式：
$∑j=0k{nm}n!(n−j)!∑i=0n−j(n−ji)\sum_{j=0}^k\begin{Bmatrix} n\\ m \end{Bmatrix}\frac{n!}{(n-j)!}\sum_{i=0}^{n-j}\binom{n-j}{i}$

$∑j=0k{kj}n!(n−j)!×2n−j\sum_{j=0}^k\begin{Bmatrix} k\\ j \end{Bmatrix}\frac{n!}{(n-j)!}\times2^{n-j}$

$O(k^2)$ 时间复杂度预处理第二类斯特林数即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5002,mod=1e9+7;
ll n,k;
ll S2[N][N],p2[N];
ll qpow(ll x,ll k)
{ll ret=1;while(k){if(k&1)ret=ret*x%mod;x=x*x%mod;k>>=1;}return ret;
}
void init()
{S2[0][0]=1;for(int i=1;i<N;i++)for(int j=1;j<N;j++)S2[i][j]=(S2[i-1][j-1]+j*S2[i-1][j]%mod)%mod;
}
int main()
{scanf("%lld%lld",&n,&k);init();ll ans=0;for(int j=0;j<=min(n,k);j++){ll ret=S2[k][j]*qpow(2,n-j)%mod,mul=1;for(int t=n-j+1;t<=n;t++)ret=ret*t%mod;ans=(ans+ret)%mod;}printf("%lld",ans);return 0;
}

第一类斯特林数

概念

$[nm]\begin{bmatrix} n\\ m \end{bmatrix}$ 表示，将 $n$ 个不同的球摆成 $m$ 个环的方案数。两个环相同，当且仅当一个环通过旋转可以变成第二个环。

其递推式的推导：

球 $n$ 单开一个环，那么剩下 $n - 1$ 个球成 $m - 1$ 个环： $[n−1m−1]\begin{bmatrix} n-1\\ m-1 \end{bmatrix}$ ；
球 $n$ 放进 $m$ 个环，在放了的 $(n - 1)$ 个球后面都可以放： $(n−1)[n−1m](n-1)\begin{bmatrix} n-1\\ m \end{bmatrix}$ 。

所以 $[nm]=[n−1m−1]+(n−1)[n−1m]\begin{bmatrix} n\\ m \end{bmatrix}=\begin{bmatrix} n-1\\ m-1 \end{bmatrix}+(n-1)\begin{bmatrix} n-1\\ m \end{bmatrix}$ 。

特别的， $[nm]=[n=0]\begin{bmatrix} n\\ m \end{bmatrix}=[n=0]$ ，中括号为艾弗森括号。

洛谷 P4609 FJOI2016 建筑师

题意

小 Z 是一个很有名的建筑师，有一天他接到了一个很奇怪的任务：在数轴上建 $n$ 个建筑，每个建筑的高度是 $1$ 到 $n$ 之间的一个整数。

小 Z 有很严重的强迫症，他不喜欢有两个建筑的高度相同。另外小 Z 觉得如果从最左边（所有建筑都在右边）看能看到 $A$ 个建筑，从最右边（所有建筑都在左边）看能看到 $B$ 个建筑，这样的建筑群有着独特的美感。现在，小 Z 想知道满足上述所有条件的建筑方案有多少种？

如果建筑 $i$ 的左(右)边没有任何建造比它高，则建筑 $i$ 可以从左(右)边看到。两种方案不同，当且仅当存在某个建筑在两种方案下的高度不同。

$\leq n \leq 50000, \ 1 \leq A, B \leq 100, \ 1 \leq T \leq 200000$ 。

思路

中间那个左右都能看见的，高度必然是极值 $n$ 。

除去中间的，左边要看到 $a - 1$ 个，右边要看到 $b - 1$ 个。不妨将能看到的和其左/右边比它矮的看成 $a - 1 + b - 1 = a + b - 2$ 个环（反正互换位置之后，尽管某些环的元素种类改变，但是环的个数不改变），就可以用第一类斯特林数的含义，将剩下 $n - 1$ 和分成 $a + b - 2$ 个环，即 $[n−1a+b−2]\begin{bmatrix} n-1\\ a+b-2 \end{bmatrix}$ 。

然后再 $a + b - 2$ 个环中选各自最大值 $a - 1$ 个，成为左边能看见的（排列方式唯一，必然是从矮到高），即 $(a+b−2a−1)\dbinom{a+b-2}{a-1}$ 。

于是答案为 $[n−1a+b−2](a+b−2a−1)\begin{bmatrix} n-1\\ a+b-2 \end{bmatrix}\dbinom{a+b-2}{a-1}$ 。

预处理第一类斯特林数即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=5e4+9,M=202,mod=1e9+7;
ll T;
ll S1[N][M],fac[N],inv[N];
ll qpow(ll x,ll k)
{ll ret=1;while(k){if(k&1)ret=ret*x%mod;x=x*x%mod;k>>=1;}return ret;
}
void init()
{S1[0][0]=1;for(int i=1;i<N;i++)for(int j=1;j<M;j++)S1[i][j]=(S1[i-1][j-1]+(i-1)*S1[i-1][j]%mod)%mod;fac[0]=1;for(int i=1;i<N;i++)fac[i]=fac[i-1]*i%mod;inv[N-1]=qpow(fac[N-1],mod-2);for(int i=N-2;i>=0;i--)inv[i]=inv[i+1]*(i+1)%mod;
}
ll C(ll n,ll m)
{return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main()
{scanf("%lld",&T);init();while(T--){ll n,a,b;scanf("%lld%lld%lld",&n,&a,&b);printf("%lld\n",S1[n-1][a+b-2]*C(a+b-2,a-1)%mod);}return 0;
}

无根树的 prufer 序列

概念

prufer 序列将节点数为 $n$ 的无根树转化为长为 $n - 2$ 的序列。其表示期望与根的编号无关——定义为每次选择一个编号最小的叶节点并删除，然后在序列中记录其所连接的节点编号，直到剩下两个节点。

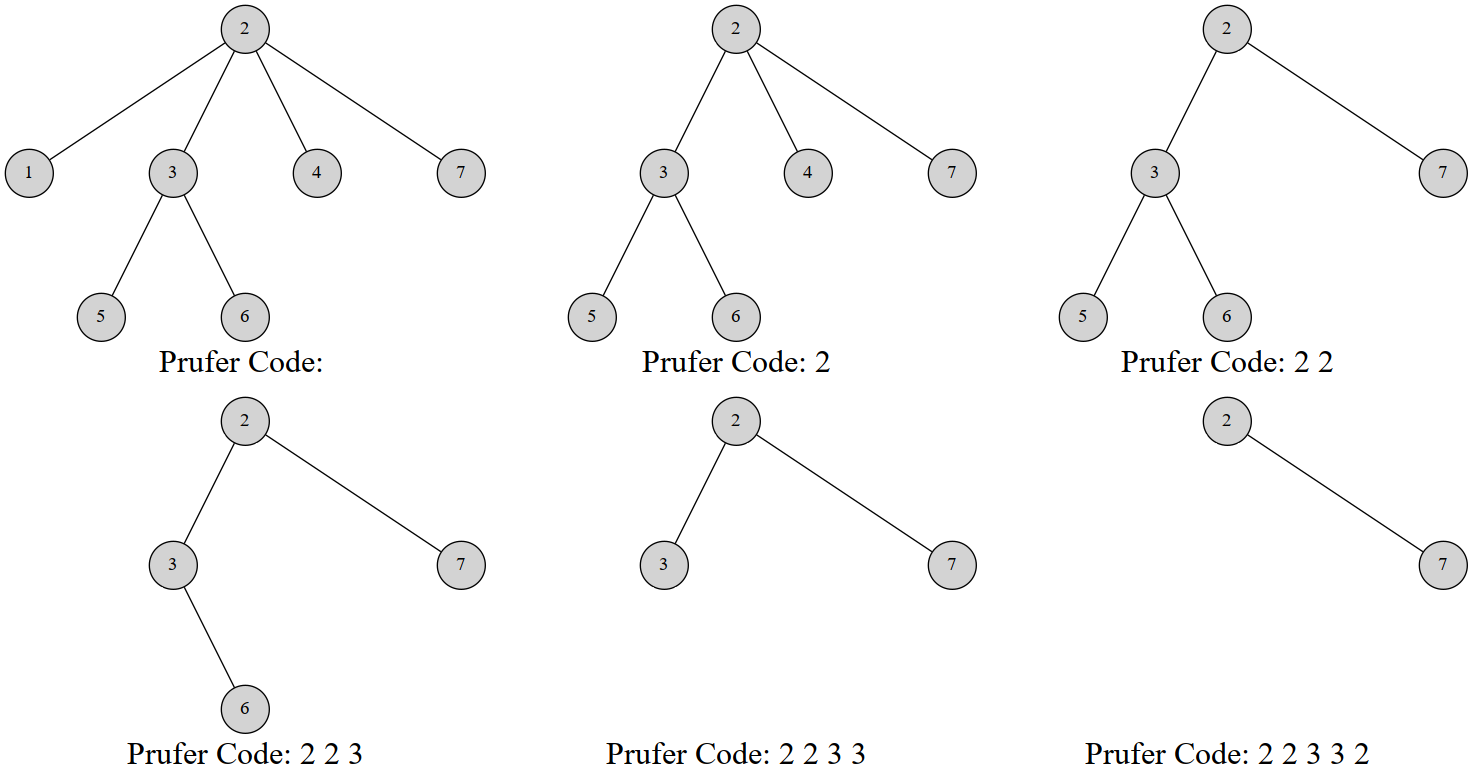
在这里插入图片描述
如上图是一棵有 $7$ 个节点的树的 prufer 序列形成过程。

用 prufer 序列同样可以还原出一棵树来。

求法

求一棵树的 prufer 序列。可以维护每个节点的度数，以节点编号为第一关键字扔进堆里排序，当度为 $0$ 时舍弃这个节点。容易做到 $O(nlog⁡n)O(n\log n)$ 。

有 $O (n)$ 的更优秀的算法：“剥叶子”的过程中，每次只会让其父亲节点度数减 $1$ ，因此每删除一个叶节点，至多产生一个新叶节点。

因此可以用一个单调指针 $p os$ 维护当前度数为 $0$ 的最小结点， $p os$ 枚举到了先删 $p os$ ，然后看 $fa_{pos}$ 是否度数变为 $0$ ，如果为 $0$ 就顺带删去了；没准是条链，因此可以 while 一路删上去。

用 prufer 还原一棵树维护序列中节点的待加边，当儿子连完、待加边归 $0$ ，就连向序列中下一个节点——似乎完全就是求 prufer 的相反操作，具体看下面的代码。

P6086 【模板】Prufer 序列

思路

如上所述。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+9;
ll n,m,mod,k;
ll fa[N],siz[N];
ll fz(ll x)
{while(x!=fa[x])x=fa[x]=fa[fa[x]];return x;
}
void join(ll u,ll v)
{ll fu=fz(u),fv=fz(v);if(fu==fv)return;fa[fu]=fv;siz[fv]+=siz[fu];k--;
}
ll qpow(ll x,ll k)
{ll ret=1;while(k){if(k&1)ret=ret*x%mod;x=x*x%mod;k>>=1;}return ret;
}
int main()
{scanf("%lld%lld%lld",&n,&m,&mod);if(mod==1){puts("0");return 0;}k=n;for(int i=1;i<=n;i++)fa[i]=i,siz[i]=1;for(int i=1;i<=m;i++){ll u,v;scanf("%lld%lld",&u,&v);join(u,v);}if(k==1){puts("1");return 0;}ll ans=1;for(int i=1;i<=n;i++)if(i==fz(i))ans=ans*siz[i]%mod;ans=ans*qpow(n,k-2)%mod;printf("%lld",ans);return 0;
}

prufer 序列怎么求其实应用不广，关键是其本身所带有的性质更为重要。

应用

把一个树化为 prufer 序列，是建立 $n$ 个节点无根树和 $n - 2$ 个元素的序列的双射。
一个节点在 prufer 序列中出现次数为其度数减 $1$ ；
Cayley 公式：对 $n$ 个节点建立一棵无根树，有 $n^{n-2}$ 种方案。

证明：任意一个长度为 $n - 2$ 的值域 $[1, n]$ 的整数序列都可以通过 prufer 序列双射对应一个生成树，于是方案数就是 $n^{n-2}$ 。

CF156D Clues

题意

给定一个 $n$ 个点 $m$ 条边的带标号无向图，若其有 $k$ 个连通块，想要添加 $k - 1$ 条边使得整个图连通。求方案数。

$1≤n≤1051\le n\le 10^5$ ， $0≤m≤1050\le m\le 10^5$ ， $1≤k≤1091\le k\le 10^9$ 。

思路

这是一道经典问题。

设每个连通块有 $s_i$ 个节点， $d_i$ 为连通块的度数—— prufer 序列就是用度数所推。

在这里插入图片描述

计算上式即可。代码略。

洛谷 P2290 HNOI2004 树的计数

题意

一个有 $n$ 个节点的树，设它的节点分别为 $v1,v2,…,vnv_1,v_2,\ldots,v_n$ ，已知第 $i$ 个节点 $v_i$ 的度数为 $d_i$ ，问满足这样的条件的不同的树有多少棵。

$1≤n≤1501\le n\le 150$ ，保证满足条件的树不超过 $10^{17}$ 个。

思路

其实方案数就是上一篇题解所提， $(n−2d1−1,d2−1,d3−1,......,dn−1)=(n−2)!∏i=1n(di−1)!\dbinom{n-2}{d_1-1,d_2-1,d_3-1,......,d_n-1}=\dfrac{(n-2)!}{\displaystyle\prod_{i=1}^n(d_i-1)!}$ 。

好像会爆 long long，阶乘的增长速度超乎想象，倒不如用它的普通组合数意义形式。设 $s_i=d_i-1$ ， $s u m = n - 2$ （理论上是 $∑si\sum s_i$ ，如果不是就不合法）。答案就是 $∏i=1n(sum−∑j=1i−1sjsi)\prod_{i=1}^n\binom{sum-\displaystyle\sum_{j=1}^{i-1}s_j}{s_i}$

代码略。

洛谷 P2624 HNOI2008 明明的烦恼

题意

给出标号为 $1$ 到 $n$ 的点，以及某些点最终的度数，允许在任意两点间连线，可产生多少棵度数满足要求的树？无解就输出 $- 1$ 。

$1≤n≤10001\le n\le1000$ 。

思路

这是上一题的加强版。

对于已知的 $m$ 个点，我们可以直接套用上面的 $(m−2d1−1,d2−1,d3−1,......,dm−1)=(m−2)!∏i=1m(di−1)!\dbinom{m-2}{d_1-1,d_2-1,d_3-1,......,d_m-1}=\dfrac{(m-2)!}{\displaystyle\prod_{i=1}^m(d_i-1)!}$ 公式，prufer 序列上已经选了的方案数为 $(n−2∑i=1m(di−1))\dbinom{n-2}{\displaystyle\sum_{i=1}^m(d_i-1)}$ ，最后再把剩下的 $n - m$ 个点，塞进 $n−2−∑i=1m(di−1)n-2-\displaystyle\sum_{i=1}^m(d_i-1)$ 去：
$(n−2∑i=1m(di−1))(m−2)!∏i=1m(di−1)!×(n−m)n−2−∑i=1m(di−1)\dbinom{n-2}{\displaystyle\sum_{i=1}^m(d_i-1)}\dfrac{(m-2)!}{\displaystyle\prod_{i=1}^m(d_i-1)!}\times(n-m)^{n-2-\displaystyle\sum_{i=1}^m(d_i-1)}$