损失函数的等高线与参数置零的关系

1. 什么是等高线？

损失函数的等高线就像地形图一样，连接所有损失值相同的点：

1. 每条等高线上的所有点都有相同的损失值
2. 内层等高线损失小，外层等高线损失大
3. 我们的目标是找到最内层的等高线（最小损失）

2. 等高线的形状差异

MAE: |θ₁| + |θ₂| = 常数 → 菱形
MSE: θ₁² + θ₂² = 常数 → 圆形

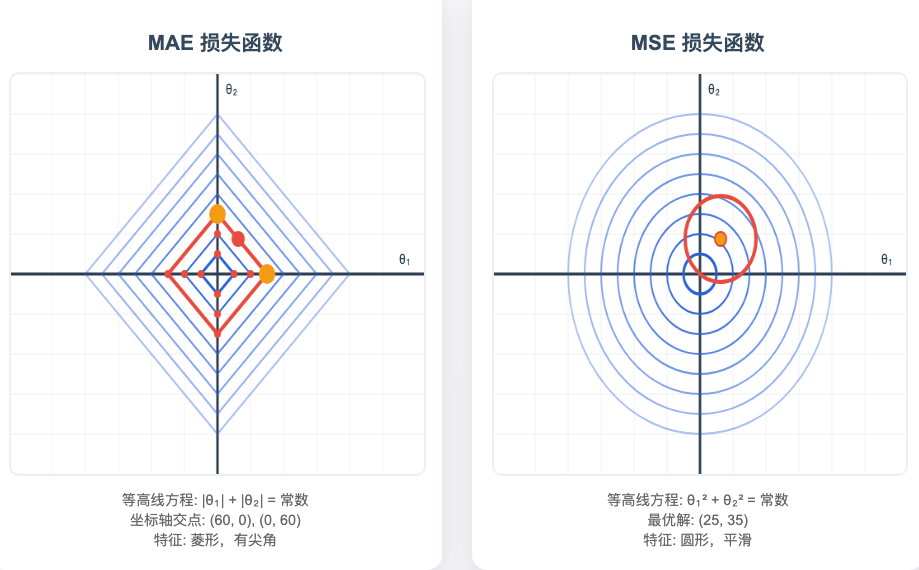
3. 逐步理解优化过程

步骤1: 理解问题设置

假设我们要找到最优参数 θ₁ 和 θ₂，使得损失函数最小。真实的最优解是红色点。

$$目标：找到{\theta }_1,{\theta }_2使得Loss({\theta }_1,{\theta }_2)最小$$

步骤2: 等高线的作用

等高线告诉我们：同一条等高线上的所有点都有相同的损失值。

• 内层等高线：损失值较小（更接近最优）
• 外层等高线：损失值较大（远离最优）

步骤3: 优化策略

优化算法的目标是找到最内层的等高线（最小损失）。但是：
$$关键洞察：当我们添加约束（如L1正则化）时，我们不能选择任意点，而是要在约束区域内找到损失最小的点。$$

步骤4: 坐标轴交点的特殊性

坐标轴上的点有特殊含义：

• θ₁轴上的点：θ₂ = 0（第二个参数被置零）
• θ₂轴上的点：θ₁ = 0（第一个参数被置零）

这就是稀疏性的来源！

特征	MAE (L1)	MSE (L2)
等高线形状	菱形（有尖角）	圆形（平滑）
坐标轴交点	在每条等高线的顶点	很少有明显交点
优化结果	倾向于选择坐标轴上的点	很少选择坐标轴上的点
参数特性	部分参数为零（稀疏）	所有参数都非零（密集）

4. 核心理解

MAE的等高线在坐标轴上形成"尖角"，这些尖角恰好是某个参数为零的位置。 当优化算法寻找最小损失时，这些尖角成为自然的"候选点"。 如果这些点的损失足够小，算法就会选择它们，从而实现参数置零。