时间复杂度和空间复杂度是衡量一个算法好坏的标准

什么是算法

        简单的说，算法就是解决问题的步骤和方法；在我们日常敲代码的过程中，会发现大部分时候一个问题是有多种解法的，那么我们如何去评价这个解法（算法）的好坏或是算法的效率呢？这时我们就得对时间复杂度和空间复杂度有一定的理解。

时间复杂度

        时间复杂度是算法时间上的效率，是衡算算法好坏的标准之一，但是它并不是说程序执行所需要用到的时间，而是通过某种函数来表达算法的复杂度，与算法中的语句执行次数有关。

 void func(int N){int count = 0;for (int i = 0; i < N; i++) {//这条语句执行的次数为n，i++会执行n次for (int j = 0; j < N; j++) {//这条语句本省会执行n次count++;//嵌套循环体执行n^2次}}for (int k = 0; k < 2*N; k++) {count++;//执行2n次}int M = 10;while ((M--)>0){//执行十次count++;}System.out.println(count);}

        上述，func内的基本操作数等于所有语句执行次数之和：F（n）=n^2+2n+10;而我们所说的时间复杂度只是一个大概的函数，相对于n^2这个函数来说，2n和10加不加影响也不大；所以我们func()时间复杂度是O（n^2）; 

大O的渐进表示算法的时间复杂度

• 格式：O(表达式)；
• 其中表达式的核心是输入规模n的最高次项，忽略低次项和常数项执行对结果影响不大的项。
• 如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
• 如果表达式只有常数阶时那么就取1代替所有常数相加

时间复杂度也分最好、最坏和平均的情况；但我们通常考虑的是最坏的情况； 

常见时间复杂度的例子:

我们需要注意的是一些递归算法的时间复杂度；大部分递归算法的时间复杂度会等于递归的次数*每次递归后执行的次数:

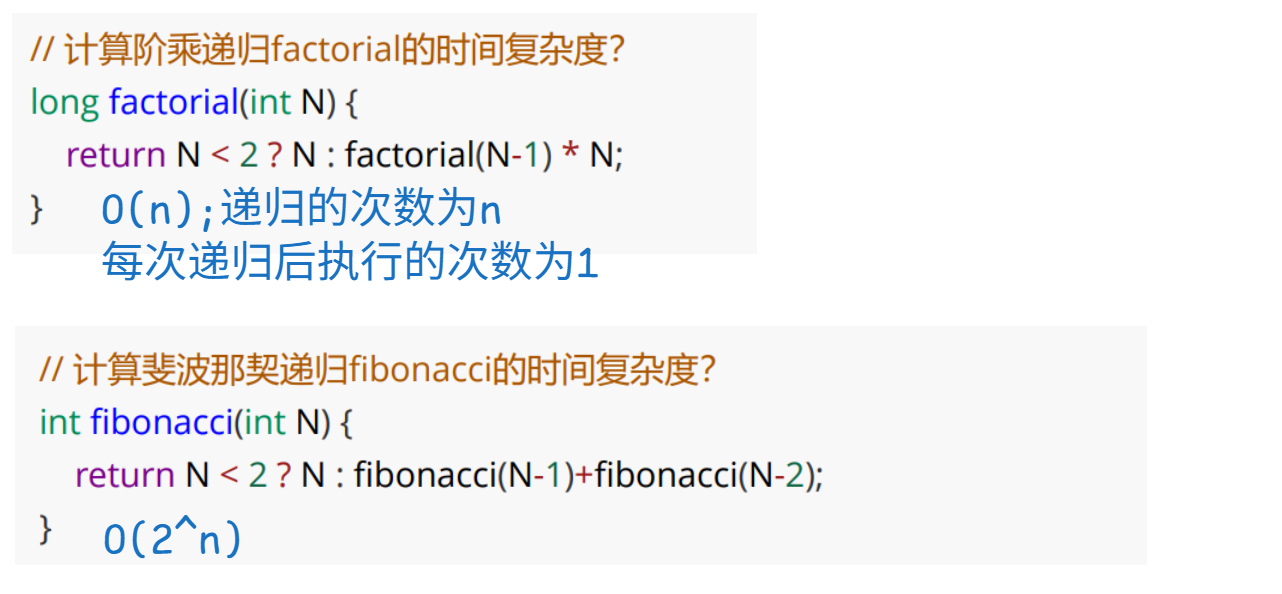常见的时间复杂度：

O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)

算法除了时间上的效率，还有评价算法好坏的另一条指标。 

空间复杂度

        空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度，可以简单的理解为除原始数据外所需的额外存储空间大小;它的表示方法基本上跟时间复杂度相同；都是通过某种函数来表达算法的复杂度，用的也是大O渐进表示法:

递归的空间复杂度主要由递归深度决定，根本原因是每次递归调用都会在内存的 调用栈中创建一个新的栈帧，这些栈帧会累积直到递归结束。后面学到栈的时候会详细说明。

---

感谢大家阅读📚点赞👍收藏⭐评论✍关注❤

博客主页： 【长毛女士-CSDN博客】

水平有限，欢迎大家纠错♥