当前位置：首页 > news >正文

【卡尔曼滤波第六期】集合变换卡尔曼滤波 ETKF

news 2025/7/16 9:35:32

集合变换卡尔曼滤波（Ensemble Transform Kalman Filter, ETKF）是一种基于集合的贝叶斯滤波方法，是集合卡尔曼滤波（Ensemble Kalman Filter, EnKF）的一个变种。它主要用于处理高维、非线性系统中的状态估计问题，在大气科学、海洋模拟、机器人导航等领域有广泛应用。

集合变换卡尔曼滤波概述

一、原理概述

ETKF 与传统 EnKF 的主要不同在于 更新集合成员的方式：

EnKF：通过对观测值引入扰动，采用蒙特卡洛方法近似后验协方差矩阵。
ETKF：通过一个 确定性线性变换来更新集合 ，不需要扰动观测值，从而避免了观测噪声引起的额外误差。

ETKF 采用 集合变换（Ensemble Transform） 的方式，将预测集合通过一个线性变换矩阵映射为分析集合。

二、数学原理

假设系统状态为 x∈R^n ，有如下步骤：

1. 初始集合
在这里插入图片描述
2. 计算观测空间中的扰动

3. 计算分析扰动的变换矩阵

4. 分析均值更新

5. 构造分析集合

最终分析集合为：
在这里插入图片描述

三、ETKF 实现步骤总结

1、初始化：生成状态初始集合。

2、预测步：

对每个集合成员进行状态传播。
计算预测均值和扰动。

3、观测空间变换：

计算预测观测集合。
计算观测扰动矩阵。

4、分析步：

构造变换矩阵 𝑇。
更新扰动和均值。
构造分析集合。

5、迭代：用分析集合作为下一时刻的预测集合。

MATLAB实现案例

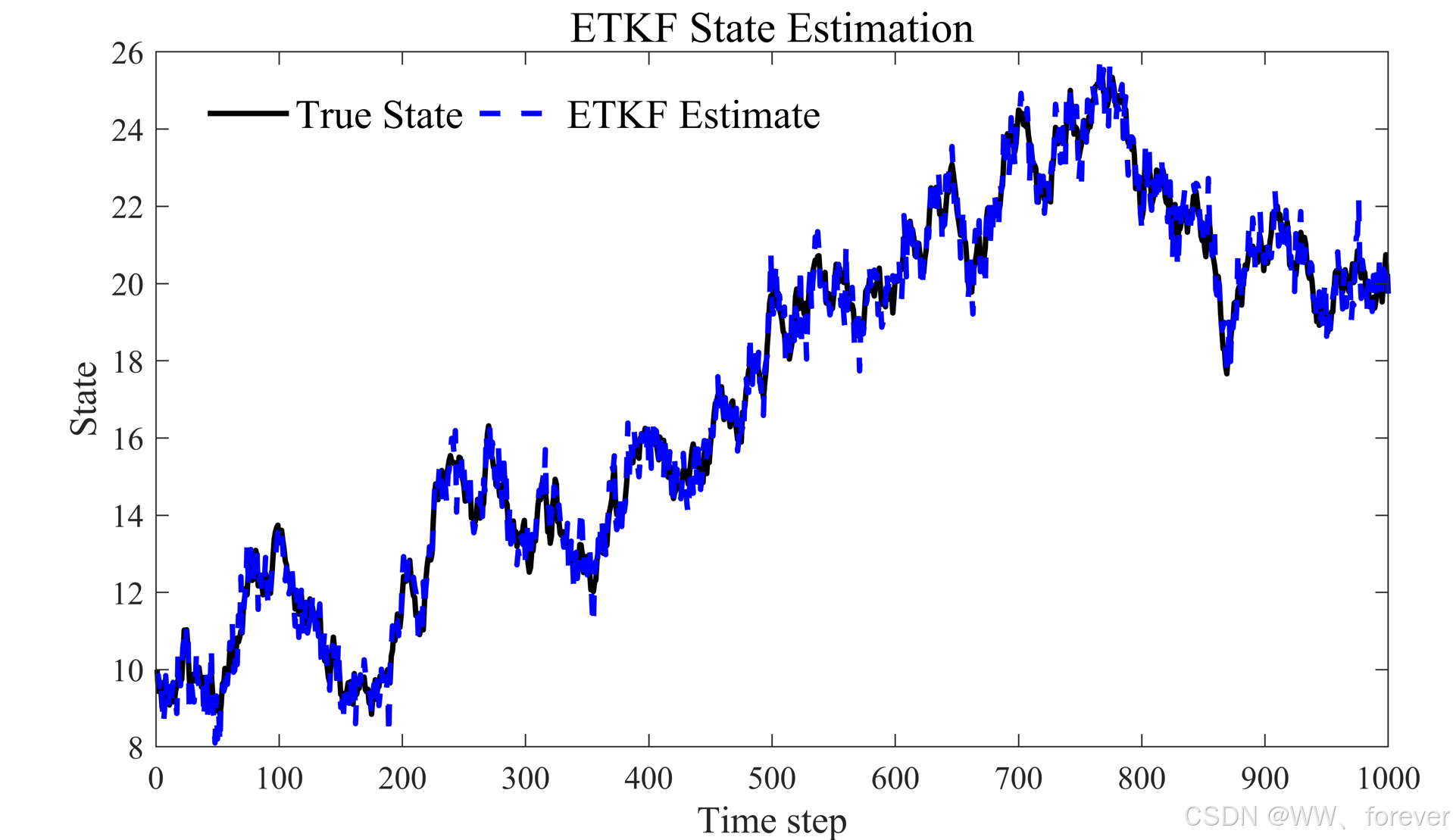
状态演变图形如下：
在这里插入图片描述
完整MATLAB代码如下：

% ETKF Demo in MATLAB
close all;
clear; 
clc;pathFigure = ".\Figures\";%% Setting
% ---------------------------------------------% Parameters
N = 50;                 % Ensemble size
n_steps = 1000;    % Time steps
Q = 0.1;                   % Process noise
R = 0.2;                    % Observation noise% True state
x_true = zeros(1, n_steps);
x_true(1) = 10;% Observations
y = zeros(1, n_steps);% Initial ensemble
Xf = 10 + sqrt(Q) * randn(1, N);% Storage
xa_mean = zeros(1, n_steps);for k = 1:n_steps% True state propagationif k > 1x_true(k) = x_true(k-1) + sqrt(Q) * randn;end% Observationy(k) = x_true(k) + sqrt(R) * randn;% Forecast step: propagate ensembleXf = Xf + sqrt(Q) * randn(1, N);% Forecast mean and perturbationsxf_mean = mean(Xf);Xf_pert = Xf - xf_mean;% Observation of ensembleYf = Xf;  % Identity observation operator H=1yf_mean = mean(Yf);Yf_pert = Yf - yf_mean;% Compute transformation matrix TS = (Yf_pert' / sqrt(R)) * (Yf_pert / sqrt(R)) / (N - 1);[U, S, V] = svd(Yf_pert / sqrt(R), 'econ');Lambda = diag(S).^2;T = U * diag(1 ./ sqrt(1 + Lambda)) * U';% Analysis perturbationsXa_pert = Xf_pert * T;% Analysis mean (corrected)dy = y(k) - yf_mean;w = T * T' * (Yf_pert' / R) * dy';xa_mean(k) = xf_mean + Xf_pert * w;% Analysis ensembleXf = xa_mean(k) + Xa_pert;
end% Plot
figure;
grid on;
plot(1:n_steps, x_true, 'k-', 'LineWidth', 2); hold on;
plot(1:n_steps, xa_mean, 'b--', 'LineWidth', 2);
set(gca, 'FontSize', 12, 'FontName', 'Times New Roman');hl = legend('True State', 'ETKF Estimate');
set(hl, 'NumColumns', 2, 'box', 'off', 'FontName', 'Times New Roman', 'FontSize', 15,'Location','north');
xlabel('Time step','FontSize',14,'FontName','Times New Roman');
ylabel('State','FontSize',14,'FontName','Times New Roman');
title('ETKF State Estimation','FontSize',16,'FontName','Times New Roman');
set(gca,'Layer','top');