catelen数到二叉树节点的联想

进出栈的组合数

王道数据结构书里说栈进出组合数的时候，让背公式把这个推导跳过去了，我去网上看分析贴又翻到用深搜递归代码来解释问题的情况，代码如下:

include<iostream>
using namespace std;
int dfs(int i,int j){if(i==0)return 1;//没有数要进栈,方案数为1int sum=0;if(j>0)sum+=dfs(i,j-1);//将一个数出栈sum+=dfs(i-1,j+1);//将一个数进栈return sum;
}
int main(){int n;cin>>n;cout<<dfs(n,0);return 0;
}

看到这个代码不知道有多少人像我一样久久困惑于递归玄学，原帖的解析如下：

我们可以考虑用递归来枚举每一种状态，对于每种状态，它可以衍生出两种状态，一:将一个数进栈，二:将栈顶出栈 所以我们就可以给d f s
dfsdfs函数设置两个参数，一个是还没有进入栈的有多少个元素和栈内现在有多少个元素 所以可以定义d f s ( i , j )
dfs(i,j)dfs(i,j)的意思是还有i个元素没有进入和j个数未出栈的总方案 这样写起来应该会写吧，主函数内调用的就是d f s (
n , 0 ) dfs(n,0)dfs(n,0)，意思是n个数还没有进栈和0个数没有出栈的总方案

我过去写LeetCode或者蓝桥杯碰到这种其实都一只半解
为什么进一个数或者出一个数就调用递归，还把返回值加到方案数，最终就能得到方案数？

终于这次停止空想开始手推这个过程
假设有初使空栈，10个数需要进栈
每一步可以选择出栈或者进栈，这其实很像一颗决策二叉树。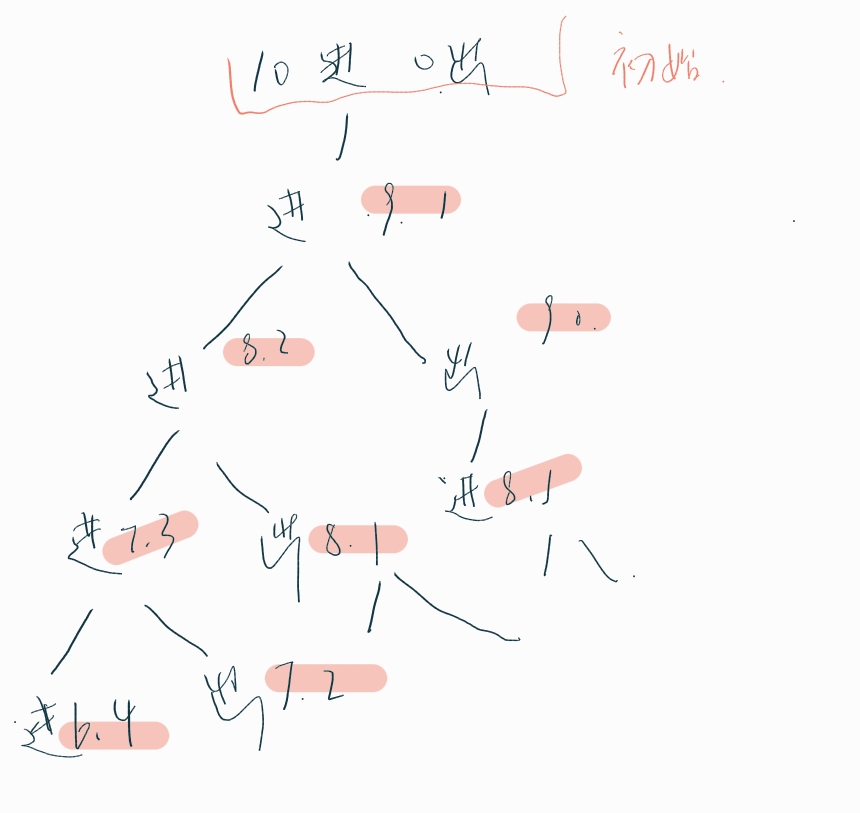
推得过程中逐渐发现，

• 代码中sum+=dfs的位置其实就是二叉树每次长出新的分叉的位置
• 每个dfs调用何时结束呢,也就是sum+1什么时候发生？那就是走到最后下面再也没有新的分叉的时候，这决定递归结束条件，是i=0,及没有新的元素需要入栈了。
• 然而每个分叉都会诞生一个新的选择方案，所以，每次dfs决定要进还是要出都加进sum里，得到叶子节点结束调用时得到返回值。
• 而每次分叉都诞生一个新的选择方案，初始状态分叉诞生两个选择，以后每次分叉诞生一个新的选择，所以分叉数+1就得到选择方案的总数。而每个方案都有最后一步，都会诞生一个叶子节点，方案数等于叶子节点的数量！并且分叉是什么？非叶子节点！