当前位置：首页 > java >正文

Python 训练营打卡 Day 33

java 2025/8/12 1:02:17

简单的神经网络

简单神经网络的流程

数据预处理（归一化、转换成张量）
模型的定义（基础nn.Module类，定义每一个层，定义向前传播过程）
定义损失函数和优化器
定义训练过程
可视化loss过程

预处理补充：

1. 分类任务中，若标签是整数（如 0/1/2 类别），需转为long类型（对应 PyTorch 的torch.long），否则交叉熵损失函数会报错

2. 回归任务中，标签需转为float类型（如torch.float32）

数据的准备与预处理

# 仍然用4特征，3分类的鸢尾花数据集作为我们今天的数据集
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import numpy as np# 加载数据集
iris = load_iris()
x = iris.data
y = iris.target
# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)
# 打印尺寸
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)# 归一化数据，神经网络对于输入数据的尺寸敏感，归一化是最常见的处理方式
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test) #确保训练集和测试集使用相同的缩放因子
# y_train和y_test是整数，所以需要转化为long类型，如果是float32，会输出1.0 0.0
x_train = torch.FloatTensor(x_train) 
y_train = torch.LongTensor(y_train)
x_test = torch.FloatTensor(x_train)
y_test = torch.LongTensor(y_train)

模型架构定义

定义一个简单的全连接神经网络模型，包含一个输入层、一个隐藏层和一个输出层

import torch.nn as nn # 导入PyTorch的神经网络模块
import torch.optim as optim # 导入PyTorch的优化器模块
class MLP(nn.Module): # 定义一个多层感知机（MLP）模型，继承父类nn.Moduledef __init__(self): # 初始化函数super(MLP, self).__init__() # 调用父类的初始化函数# 定义的前三行是八股文，后面的是自定义的self.fc1 = nn.Linear(4, 10) # 定义第一个全连接层，输入维度为4，输出维度为10self.relu = nn.ReLU() # 定义激活函数ReLUself.fc2 = nn.Linear(10, 3) # 定义第二个全连接层，输入维度为10，输出维度为3
# 输出层不需要激活函数，因为后面会用到交叉熵函数cross_entropy，交叉熵函数内部有softmax函数，会把输出转化为概率def forward(self, x):out = self.fc1(x) # 输入x经过第一个全连接层out = self.relu(out) # 激活函数ReLUout = self.fc2(out) # 输入out经过第二个全连接层return out # 返回输出# 实例化模型
model = MLP() # 实例化模型，得到一个对象model

网络结构说明：

- 输入层：4个神经元（对应4维特征）
- 隐藏层：10个神经元 + ReLU激活
- 输出层：3个神经元（对应3分类问题）
- 总参数量：(4×10 + 10) + (10×3 + 3) = 83个参数

模型训练

# 定义损失函数和优化器
# 分类问题使用交叉熵损失函数，适用于多分类问题，应用softmax函数将输出映射到概率分布，然后计算交叉熵损失
criterion = nn.CrossEntropyLoss()
# 使用随机梯度下降优化器（SGD)，学习率为0.01
optimizer = optim.SGD(model.parameters(), lr=0.01)

在前面感知机模型的基础上又借用了SoftMax模型，因为感知机模型和SoftMax在分类任务中是配合使用的，它们的关系可以这样理解：

1. 感知机的作用：
- 前面的MLP模型（多层感知机）是一个基础神经网络
- 它通过全连接层(fc1, fc2)进行特征变换
- 最终输出的是未归一化的"原始分数"(logits)
2. 为什么需要Softmax ：
- 分类问题需要输出概率分布(各类别概率和为1)
- CrossEntropyLoss内部自动集成了Softmax
- 将前面得到的logits最终转换为概率分布：exp(logit)/sum(exp(logits))

# 开始循环训练
# 训练模型
num_epochs = 20000 # 训练的轮数# 用于存储每个 epoch 的损失值
losses = []for epoch in range(num_epochs): # 开始迭代训练过程，range是从0开始，所以epoch是从0开始# 前向传播：将数据输入模型，计算模型预测输出outputs = model.forward(x_train)   # 显式调用forward函数# outputs = model(X_train)  # 常见写法隐式调用forward函数，其实是用了model类的__call__方法loss = criterion(outputs, y_train) # output是模型预测值，y_train是真实标签，计算两者之间损失值# 反向传播和优化optimizer.zero_grad() #梯度清零，因为PyTorch会累积梯度，所以每次迭代需要清零，梯度累计是那种小的bitchsize模拟大的bitchsizeloss.backward() # 反向传播计算梯度，自动完成以下计算：# 1. 计算损失函数对输出的梯度# 2. 从输出层→隐藏层→输入层反向传播# 3. 计算各层权重/偏置的梯度optimizer.step() # 更新参数# 记录损失值losses.append(loss.item())# 打印训练信息if (epoch + 1) % 100 == 0: # range是从0开始，所以epoch+1是从当前epoch开始，每100个epoch打印一次print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

打印结果为：

Epoch [100/20000], Loss: 1.1227
Epoch [200/20000], Loss: 1.0643
Epoch [300/20000], Loss: 1.0096
Epoch [400/20000], Loss: 0.9506
Epoch [500/20000], Loss: 0.8840
Epoch [600/20000], Loss: 0.8132
Epoch [700/20000], Loss: 0.7441
Epoch [800/20000], Loss: 0.6815
Epoch [900/20000], Loss: 0.6280
Epoch [1000/20000], Loss: 0.5836
Epoch [1100/20000], Loss: 0.5470
Epoch [1200/20000], Loss: 0.5168
Epoch [1300/20000], Loss: 0.4914
Epoch [1400/20000], Loss: 0.4695
Epoch [1500/20000], Loss: 0.4500
Epoch [1600/20000], Loss: 0.4323
Epoch [1700/20000], Loss: 0.4161
Epoch [1800/20000], Loss: 0.4009
Epoch [1900/20000], Loss: 0.3866
Epoch [2000/20000], Loss: 0.3731
Epoch [2100/20000], Loss: 0.3601
Epoch [2200/20000], Loss: 0.3478
Epoch [2300/20000], Loss: 0.3360
Epoch [2400/20000], Loss: 0.3246
Epoch [2500/20000], Loss: 0.3137
Epoch [2600/20000], Loss: 0.3033
Epoch [2700/20000], Loss: 0.2933
Epoch [2800/20000], Loss: 0.2837
Epoch [2900/20000], Loss: 0.2746
Epoch [3000/20000], Loss: 0.2658
Epoch [3100/20000], Loss: 0.2575
Epoch [3200/20000], Loss: 0.2496
Epoch [3300/20000], Loss: 0.2420
Epoch [3400/20000], Loss: 0.2348
Epoch [3500/20000], Loss: 0.2280
Epoch [3600/20000], Loss: 0.2215
Epoch [3700/20000], Loss: 0.2152
Epoch [3800/20000], Loss: 0.2093
Epoch [3900/20000], Loss: 0.2037
Epoch [4000/20000], Loss: 0.1983
Epoch [4100/20000], Loss: 0.1932
Epoch [4200/20000], Loss: 0.1884
Epoch [4300/20000], Loss: 0.1837
Epoch [4400/20000], Loss: 0.1793
Epoch [4500/20000], Loss: 0.1751
Epoch [4600/20000], Loss: 0.1711
Epoch [4700/20000], Loss: 0.1673
Epoch [4800/20000], Loss: 0.1637
Epoch [4900/20000], Loss: 0.1602
Epoch [5000/20000], Loss: 0.1568
Epoch [5100/20000], Loss: 0.1536
Epoch [5200/20000], Loss: 0.1506
Epoch [5300/20000], Loss: 0.1477
Epoch [5400/20000], Loss: 0.1449
Epoch [5500/20000], Loss: 0.1422
Epoch [5600/20000], Loss: 0.1396
Epoch [5700/20000], Loss: 0.1372
Epoch [5800/20000], Loss: 0.1348
Epoch [5900/20000], Loss: 0.1326
Epoch [6000/20000], Loss: 0.1304
Epoch [6100/20000], Loss: 0.1283
Epoch [6200/20000], Loss: 0.1263
Epoch [6300/20000], Loss: 0.1244
Epoch [6400/20000], Loss: 0.1225
Epoch [6500/20000], Loss: 0.1207
Epoch [6600/20000], Loss: 0.1190
Epoch [6700/20000], Loss: 0.1174
Epoch [6800/20000], Loss: 0.1158
Epoch [6900/20000], Loss: 0.1142
Epoch [7000/20000], Loss: 0.1128
Epoch [7100/20000], Loss: 0.1113
Epoch [7200/20000], Loss: 0.1100
Epoch [7300/20000], Loss: 0.1086
Epoch [7400/20000], Loss: 0.1073
Epoch [7500/20000], Loss: 0.1061
Epoch [7600/20000], Loss: 0.1049
Epoch [7700/20000], Loss: 0.1037
Epoch [7800/20000], Loss: 0.1026
Epoch [7900/20000], Loss: 0.1015
Epoch [8000/20000], Loss: 0.1004
Epoch [8100/20000], Loss: 0.0994
Epoch [8200/20000], Loss: 0.0984
Epoch [8300/20000], Loss: 0.0975
Epoch [8400/20000], Loss: 0.0965
Epoch [8500/20000], Loss: 0.0956
Epoch [8600/20000], Loss: 0.0948
Epoch [8700/20000], Loss: 0.0939
Epoch [8800/20000], Loss: 0.0931
Epoch [8900/20000], Loss: 0.0923
Epoch [9000/20000], Loss: 0.0915
Epoch [9100/20000], Loss: 0.0908
Epoch [9200/20000], Loss: 0.0900
Epoch [9300/20000], Loss: 0.0893
Epoch [9400/20000], Loss: 0.0886
Epoch [9500/20000], Loss: 0.0879
Epoch [9600/20000], Loss: 0.0873
Epoch [9700/20000], Loss: 0.0866
Epoch [9800/20000], Loss: 0.0860
Epoch [9900/20000], Loss: 0.0854
Epoch [10000/20000], Loss: 0.0848
Epoch [10100/20000], Loss: 0.0843
Epoch [10200/20000], Loss: 0.0837
Epoch [10300/20000], Loss: 0.0831
Epoch [10400/20000], Loss: 0.0826
Epoch [10500/20000], Loss: 0.0821
Epoch [10600/20000], Loss: 0.0816
Epoch [10700/20000], Loss: 0.0811
Epoch [10800/20000], Loss: 0.0806
Epoch [10900/20000], Loss: 0.0801
Epoch [11000/20000], Loss: 0.0797
Epoch [11100/20000], Loss: 0.0792
Epoch [11200/20000], Loss: 0.0788
Epoch [11300/20000], Loss: 0.0784
Epoch [11400/20000], Loss: 0.0780
Epoch [11500/20000], Loss: 0.0776
Epoch [11600/20000], Loss: 0.0772
Epoch [11700/20000], Loss: 0.0768
Epoch [11800/20000], Loss: 0.0764
Epoch [11900/20000], Loss: 0.0760
Epoch [12000/20000], Loss: 0.0756
Epoch [12100/20000], Loss: 0.0753
Epoch [12200/20000], Loss: 0.0749
Epoch [12300/20000], Loss: 0.0746
Epoch [12400/20000], Loss: 0.0743
Epoch [12500/20000], Loss: 0.0739
Epoch [12600/20000], Loss: 0.0736
Epoch [12700/20000], Loss: 0.0733
Epoch [12800/20000], Loss: 0.0730
Epoch [12900/20000], Loss: 0.0727
Epoch [13000/20000], Loss: 0.0724
Epoch [13100/20000], Loss: 0.0721
Epoch [13200/20000], Loss: 0.0718
Epoch [13300/20000], Loss: 0.0716
Epoch [13400/20000], Loss: 0.0713
Epoch [13500/20000], Loss: 0.0710
Epoch [13600/20000], Loss: 0.0707
Epoch [13700/20000], Loss: 0.0705
Epoch [13800/20000], Loss: 0.0702
Epoch [13900/20000], Loss: 0.0700
Epoch [14000/20000], Loss: 0.0697
Epoch [14100/20000], Loss: 0.0695
Epoch [14200/20000], Loss: 0.0693
Epoch [14300/20000], Loss: 0.0690
Epoch [14400/20000], Loss: 0.0688
Epoch [14500/20000], Loss: 0.0686
Epoch [14600/20000], Loss: 0.0684
Epoch [14700/20000], Loss: 0.0682
Epoch [14800/20000], Loss: 0.0680
Epoch [14900/20000], Loss: 0.0677
Epoch [15000/20000], Loss: 0.0675
Epoch [15100/20000], Loss: 0.0673
Epoch [15200/20000], Loss: 0.0671
Epoch [15300/20000], Loss: 0.0670
Epoch [15400/20000], Loss: 0.0668
Epoch [15500/20000], Loss: 0.0666
Epoch [15600/20000], Loss: 0.0664
Epoch [15700/20000], Loss: 0.0662
Epoch [15800/20000], Loss: 0.0660
Epoch [15900/20000], Loss: 0.0659
Epoch [16000/20000], Loss: 0.0657
Epoch [16100/20000], Loss: 0.0655
Epoch [16200/20000], Loss: 0.0653
Epoch [16300/20000], Loss: 0.0652
Epoch [16400/20000], Loss: 0.0650
Epoch [16500/20000], Loss: 0.0649
Epoch [16600/20000], Loss: 0.0647
Epoch [16700/20000], Loss: 0.0645
Epoch [16800/20000], Loss: 0.0644
Epoch [16900/20000], Loss: 0.0642
Epoch [17000/20000], Loss: 0.0641
Epoch [17100/20000], Loss: 0.0640
Epoch [17200/20000], Loss: 0.0638
Epoch [17300/20000], Loss: 0.0637
Epoch [17400/20000], Loss: 0.0635
Epoch [17500/20000], Loss: 0.0634
Epoch [17600/20000], Loss: 0.0633
Epoch [17700/20000], Loss: 0.0631
Epoch [17800/20000], Loss: 0.0630
Epoch [17900/20000], Loss: 0.0629
Epoch [18000/20000], Loss: 0.0627
Epoch [18100/20000], Loss: 0.0626
Epoch [18200/20000], Loss: 0.0625
Epoch [18300/20000], Loss: 0.0624
Epoch [18400/20000], Loss: 0.0622
Epoch [18500/20000], Loss: 0.0621
Epoch [18600/20000], Loss: 0.0620
Epoch [18700/20000], Loss: 0.0619
Epoch [18800/20000], Loss: 0.0618
Epoch [18900/20000], Loss: 0.0617
Epoch [19000/20000], Loss: 0.0615
Epoch [19100/20000], Loss: 0.0614
Epoch [19200/20000], Loss: 0.0613
Epoch [19300/20000], Loss: 0.0612
Epoch [19400/20000], Loss: 0.0611
Epoch [19500/20000], Loss: 0.0610
Epoch [19600/20000], Loss: 0.0609
Epoch [19700/20000], Loss: 0.0608
Epoch [19800/20000], Loss: 0.0607
Epoch [19900/20000], Loss: 0.0606
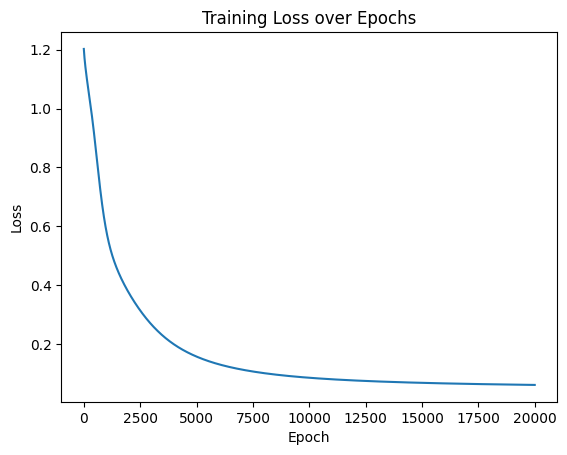
Epoch [20000/20000], Loss: 0.0605

可视化结果

import matplotlib.pyplot as plt
# 可视化损失曲线
plt.plot(range(num_epochs), losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss over Epochs')
plt.show()