Mamba 原理汇总2
Mamba 原理汇总2
- 1、原理
- 1. 什么是 Mamba?
- 2. **Mamba 的核心原理**
- 2.1 **传统状态空间模型 (SSMs)**
- 2.2 **选择性 SSM(Selective SSM)**
- 2.3 **离散化与高效计算**
- 2.4 **Mamba 架构**
- 2. Mamba 的三大核心创新
- 3. 性能与对比优势
- 5. **实际应用与实现**
- 6. **局限性与未来方向**
- 2、SSM和lstm区别
- 1. **原理差别**
- **核心原理**
- **SSM(状态空间模型)**
- **LSTM**
- 2. **结构差别**
- 3. **特性差别**
- 4. **应用差别**
- 5. **详细对比**
- **3.1 计算效率**
- **3.2 长序列建模**
- **3.3 动态性**
- **3.4 训练与优化**
- 3、并行扫描
- 1. 原理:为什么能并行
- 1.1 并行化的关键
- 2. 与 LSTM 对比
- 3. 并行扫描的具体数值例子
- 4. 直观类比
- 5. 在 Mamba 中的优化
- 1. 先理解“并行扫描”指什么
- 2. Mamba 的关键:线性状态空间模型 (SSM) 的结构
- 4、Mamba系列
- 1. Mamba(原始版本)
- 2. Mamba-2(基于 SSD 的新版)
- 3. 其他 Mamba 变体与应用案例
- 总结一览表
- 时间系列Mamba
- 1. **S-Mamba(Simple-Mamba)**
- 2. **MambaTS**
- 3. **Bi-Mamba+**
- 4. **ms-Mamba(Multi-scale Mamba)**
- 5. **SOR-Mamba(Sequential Order-Robust Mamba)**
- 6. **Attention Mamba**
- 7. **SpectroMamba(包括 BV-Mamba)**
- 8. **Mamba-ProbTSF(Uncertainty Quantification)**
- 总览对比表
- 5、Mamba2
- 概览(一句话)
- 关键符号与起点(约定)
- 把 SSM 展成矩阵 —— semiseparable 表示(关键公式)
- 标量-单位(scalar-identity)情形 — SSD 的核心代数等价
- 两种计算次序(dual algorithms):线性形式 vs 二次形式(及其等价)
- Mamba-2 在算法/实现层面的优化(简要公式化说明)
- 把上面内容串成一个紧凑推导(供 copy-paste 的主要公式)
- 参考(进一步读物)
- Mamba-2 原理教程:详细公式说明
- 1. **背景与核心创新**
- 2. **选择性 SSM 的数学基础**
- 3. **状态空间二元性(SSD):与注意力的等价性**
- 4. **高效算法与优化**
- 5. **Mamba-2 架构与对比**
- 6. **总结**
- 6、Mamba-2中n和p,和注意力机制对应关系
- 1. Mamba-2 中的 nnn 和 ppp
- 2. 对应到注意力机制
- 3. 数学对应点
- 4. 总结类比表
- 5. 注意头的数量和维度计算关系
- 1. 基本变量
- 2. 维度分配公式
- 2.1 每头的输入维度
- 2.2 每头的状态维度
- 2.3 参数矩阵大小
- 3. 和多头注意力的类比
- 4. 计算示例
- 5. 设计经验
1、原理
Mamba原理汇总1笔记:https://blog.csdn.net/weixin_44986037/article/details/147286067?
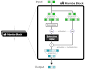
这是 Mamba 架构中常见的模型结构示意图,有助于直观理解其模块组合与信息流。以下为你系统整理的 Mamba 原理教程,帮助你从零开始入门:
1. 什么是 Mamba?
- Mamba 是一个用于序列建模的深度学习架构,由卡内基梅隆大学与普林斯顿大学的研究团队提出,旨在替代 Transformer 模型在长序列处理时面临的计算复杂性和效率瓶颈 (维基百科, 维基百科)。
- 它基于 结构化状态空间序列模型(S4),同时引入了动态选择机制,使其参数能够根据输入进行自适应调整,从而更高效地处理冗余和相关信息 (维基百科, arXiv)。
2. Mamba 的核心原理
Mamba Block架构:
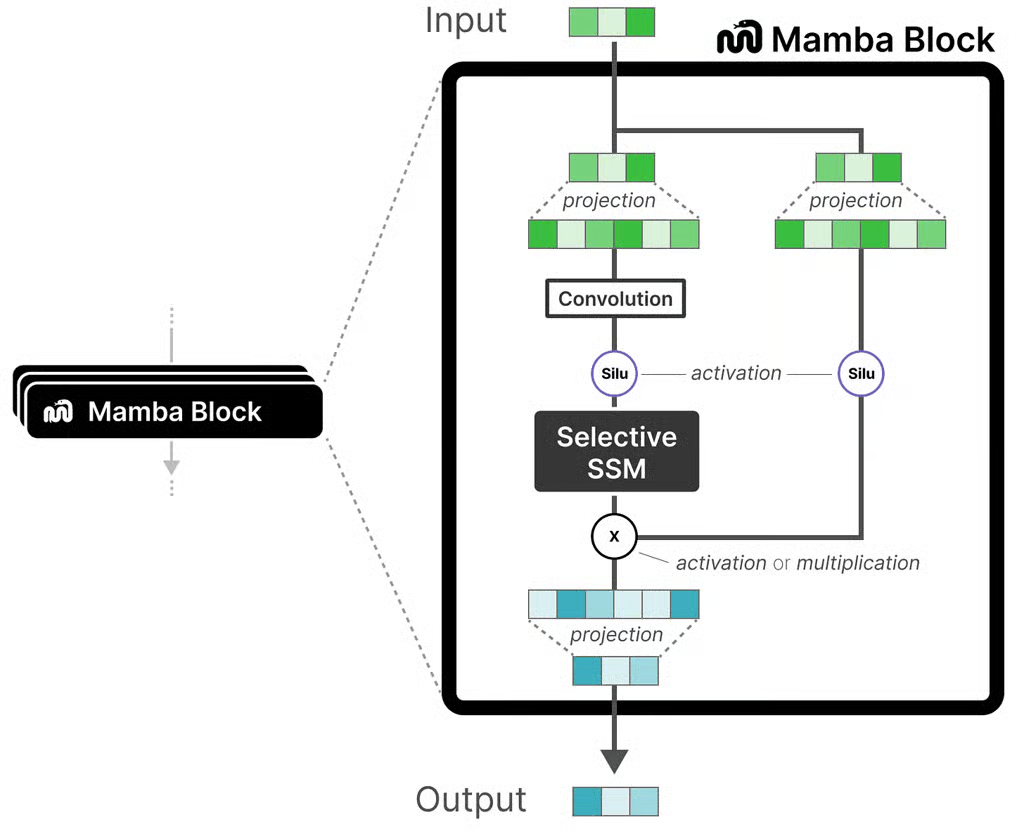
输入 x↓
LayerNorm↓
线性投影 → [x1, x2] (分支)↓ ↓
SSM处理 SiLU激活↓ ↓←——————————乘法↓
线性投影↓
残差连接↓
输出
Mamba 的核心是一个 选择性状态空间模型(Selective SSM),通过动态选择输入相关的状态,增强了传统 SSM 的表达能力。以下是其关键组件:
2.1 传统状态空间模型 (SSMs)
SSMs 基于连续系统的状态演化,形式化如下:
ht=Aht−1+Bxth_t = A h_{t-1} + B x_t ht=Aht−1+Bxt
yt=Chty_t = C h_t yt=Cht
- xtx_txt:输入序列在时间 ttt 的值。
- hth_tht:隐状态,捕捉序列历史信息。
- yty_tyt:输出。
- A,B,CA, B, CA,B,C:状态转移矩阵、输入矩阵和输出矩阵。
传统 SSM 的问题是 A,B,CA, B, CA,B,C 是固定的,缺乏对输入的动态调整能力,导致建模复杂序列时效果有限。
2.2 选择性 SSM(Selective SSM)
Mamba 引入了 选择性机制,使 BBB 和 CCC 矩阵以及时间步长 Δ\DeltaΔ 依赖于输入 xtx_txt。具体形式为:
Bt=fB(xt),Ct=fC(xt),Δt=fΔ(xt)B_t = f_B(x_t), \quad C_t = f_C(x_t), \quad \Delta_t = f_\Delta(x_t) Bt=fB(xt),Ct=fC(xt),Δt=fΔ(xt)
- fB,fC,fΔf_B, f_C, f_\DeltafB,fC,fΔ:通过神经网络(如 MLP)对输入 xtx_txt 进行建模,动态生成参数。
- Δt\Delta_tΔt:控制离散化步长,影响状态转移的动态性。
通过这种选择性机制,Mamba 能够根据输入内容动态调整状态更新,增强了对复杂序列的建模能力。
2.3 离散化与高效计算
为了在离散序列上应用 SSM,Mamba 将连续状态空间模型离散化:
Aˉ=exp(ΔtA),Bˉ=(ΔtA)−1(exp(ΔtA)−I)⋅ΔtBt\bar{A} = \exp(\Delta_t A), \quad \bar{B} = (\Delta_t A)^{-1} (\exp(\Delta_t A) - I) \cdot \Delta_t B_t Aˉ=exp(ΔtA),Bˉ=(ΔtA)−1(exp(ΔtA)−I)⋅ΔtBt
- Aˉ,Bˉ\bar{A}, \bar{B}Aˉ,Bˉ:离散化的状态转移和输入矩阵。
- 离散化后的模型可以通过卷积或递归方式计算,复杂度为 O(n)O(n)O(n),远低于 Transformer 的 O(n2)O(n^2)O(n2)。
Mamba 使用了一种 硬件加速的并行扫描算法(parallel scan),进一步优化了计算效率,特别适合 GPU 实现。
2.4 Mamba 架构
Mamba 的整体架构是一个基于选择性 SSM 的模块,堆叠多层形成深度网络:
- 输入嵌入:将输入序列映射到高维表示。
- Mamba 模块:
- 包含选择性 SSM 核心,动态生成 Bt,Ct,ΔtB_t, C_t, \Delta_tBt,Ct,Δt。
- 结合线性变换、激活函数(如 SiLU)和归一化层(如 LayerNorm)。
- 可选择性地加入残差连接,增强训练稳定性。
- 输出层:将 SSM 的输出映射到任务特定的表示(如分类、生成等)。
Mamba 模块可以看作是 Transformer 中自注意力层的替代品,但计算效率更高,适合长序列。
2. Mamba 的三大核心创新
-
选择性状态空间(Selective SSM)
- 与传统时间不变的 SSM 相比,Mamba 根据当前输入动态调整模型参数,选择性保留或遗忘信息,使其在内容理解和长期依赖建模上更具优势 (arXiv, CSDN博客, 维基百科)。
-
硬件感知算法(Hardware-aware Parallel Algorithm)
- 为提升 GPU 上的运行效率,Mamba 采用诸如内核融合(kernel fusion)、并行扫描(parallel scan)和重计算(recomputation)等技术,以减少内存访问和显存占用,显著提升推理速度与扩展效率 (arXiv, CSDN博客, 维基百科)。
-
简化统一的模型结构
- Mamba 将传统模型中的注意力机制与 MLP 块整合为简洁的 SSM 模块,使模型结构更统一轻量,适应多种数据类型(如语言、音频、基因组等) (CSDN博客, 维基百科)。
3. 性能与对比优势
| 特性 | Transformer | Mamba |
|---|---|---|
| 模型结构 | 注意力 + MLP | 单一 SSM 模块 |
| 推理时间复杂度 | O(n) | O(1)(线性时间) |
| 训练时间复杂度 | O(n²) | O(n) |
| 序列长度扩展性 | 限制较大 | 极强,可处理百万级长度 (维基百科, arXiv) |
- Mamba 推理速度比同规模 Transformer 快约 5 倍,在长序列任务(如文本、音频、基因组)上展现出强大的性能优势;在语言建模任务上,Mamba-3B 能匹配 2 倍体量的 Transformer 表现 (arXiv, The Gradient)。
5. 实际应用与实现
- 语言建模:Mamba 在语言任务(如文本生成)上表现出色,性能接近甚至超过 Transformer,同时支持更长的上下文。
- 时间序列:Mamba 的状态空间特性使其天然适合时间序列预测,如金融数据分析、传感器数据处理。
- 开源实现:Mamba 的官方实现基于 PyTorch,代码开源(例如 GitHub 上 Mamba 仓库)。核心组件包括选择性 SSM 模块和并行扫描算法。
6. 局限性与未来方向
- 局限性:
- 选择性机制的动态性可能增加训练复杂度,需精心调参。
- 对某些需要全局上下文的任务(如机器翻译),可能需要额外设计。
- 未来方向:
- 结合 Transformer 和 Mamba 的混合架构,兼顾全局和局部建模。
- 进一步优化并行扫描算法,提升在边缘设备上的效率。
局限性
表达能力: 理论上可能不如Transformer在某些任务上的表达能力
训练稳定性: 状态空间模型的训练可能比较敏感
生态系统: 相比Transformer生态系统还不够成熟
2、SSM和lstm区别
SSM和lstm区别
SSM(State Space Model,状态空间模型)和 LSTM(Long Short-Term Memory)都是处理序列数据的模型,但它们的数学基础、信息存储方式、并行化能力和适用场景差别很大。
我帮你从原理 → 结构 → 特性 → 应用四个维度对比。
1. 原理差别
| SSM(状态空间模型) | LSTM(长短期记忆网络) | |
|---|---|---|
| 数学基础 | 基于线性系统理论,用一组一阶线性微分方程(连续时间)或差分方程(离散时间)描述序列的动态变化。核心是: xt+1=Axt+But,yt=Cxt+Dutx_{t+1} = A x_t + B u_t,\quad y_t = C x_t + D u_txt+1=Axt+But,yt=Cxt+Dut 其中 xtx_txt 是隐藏状态,utu_tut 是输入,yty_tyt 是输出。 | 基于循环神经网络(RNN),通过非线性门控结构(输入门、遗忘门、输出门)控制信息流动,解决 RNN 的梯度消失/爆炸问题。核心是: ht,ct=LSTMCell(xt,ht−1,ct−1)h_t, c_t = \text{LSTMCell}(x_t, h_{t-1}, c_{t-1})ht,ct=LSTMCell(xt,ht−1,ct−1) |
| 建模方式 | 本质是对信号进行卷积运算(输入序列与系统冲激响应相乘求和),可用 FFT 或特殊矩阵快速实现。 | 每一步依赖上一步的输出,信息通过递归更新存储在细胞状态 ctc_tct 中。 |
| 记忆机制 | 状态 xtx_txt 是高维向量,可存储长期依赖;参数矩阵 A,B,C,DA,B,C,DA,B,C,D 控制信息的传递和衰减。 | 通过遗忘门调节旧信息衰减,通过输入门更新新信息,通过输出门控制隐藏状态的暴露。 |
核心原理
SSM(状态空间模型)
- 定义:SSM 基于连续系统的状态演化,形式为:
ht=Aht−1+Bxt,yt=Chth_t = A h_{t-1} + B x_t, \quad y_t = C h_t ht=Aht−1+Bxt,yt=Cht
其中 hth_tht 是隐状态,xtx_txt 是输入,yty_tyt 是输出,A,B,CA, B, CA,B,C 是状态转移、输入和输出矩阵。 - 选择性 SSM(Mamba 等):参数 B,CB, CB,C 和时间步长 Δ\DeltaΔ 可根据输入动态调整,增强表达能力。
- 特点:基于线性系统的数学框架,适合连续或离散序列,计算可通过递归或卷积实现。
LSTM
- 定义:LSTM 是一种特殊的循环神经网络(RNN),通过门控机制(输入门、遗忘门、输出门)管理长期和短期记忆:
ft=σ(Wfxt+Ufht−1+bf)(遗忘门)f_t = \sigma(W_f x_t + U_f h_{t-1} + b_f) \quad (\text{遗忘门}) ft=σ(Wfxt+Ufht−1+bf)(遗忘门)
it=σ(Wixt+Uiht−1+bi)(输入门)i_t = \sigma(W_i x_t + U_i h_{t-1} + b_i) \quad (\text{输入门}) it=σ(Wixt+Uiht−1+bi)(输入门)
ot=σ(Woxt+Uoht−1+bo)(输出门)o_t = \sigma(W_o x_t + U_o h_{t-1} + b_o) \quad (\text{输出门}) ot=σ(Woxt+Uoht−1+bo)(输出门)
ct=ft⋅ct−1+it⋅tanh(Wcxt+Ucht−1+bc)c_t = f_t \cdot c_{t-1} + i_t \cdot \tanh(W_c x_t + U_c h_{t-1} + b_c) ct=ft⋅ct−1+it⋅tanh(Wcxt+Ucht−1+bc)
ht=ot⋅tanh(ct)h_t = o_t \cdot \tanh(c_t) ht=ot⋅tanh(ct)
其中 ctc_tct 是单元状态,hth_tht 是隐状态。
- 特点:通过门控机制显式管理记忆,缓解 RNN 的梯度消失问题。
2. 结构差别
-
SSM
- 类似“物理系统”或“信号滤波器”的结构
- 输入经过线性系统(状态更新)+ 读出层得到输出
- 可以直接用矩阵指数运算模拟长时间跨度的状态传播
- 在深度学习中,SSM 通常作为卷积层的泛化(如 S4、Mamba)
-
LSTM
- 每个时间步都有三个门(输入门、遗忘门、输出门)
- 非线性计算较多(sigmoid、tanh)
- 天然适合逐步处理数据,但难并行
3. 特性差别
| 特性 | SSM | LSTM |
|---|---|---|
| 并行化 | 强 → 可一次性计算整条序列的输出(矩阵或卷积实现) | 弱 → 只能按时间步递归计算,难以并行 |
| 长序列能力 | 优秀 → 数学上可稳定传播百万步(特别是 Mamba、S4 改进后) | 容易遗忘远处信息(虽然比普通 RNN 好,但几十步后仍衰减明显) |
| 参数效率 | 高 → 相同参数下可处理更长依赖 | 中 → 每步都有额外门控计算 |
| 可解释性 | 强 → 系统矩阵的谱分解、时间常数可解释物理含义 | 弱 → 门控权重难直接解释 |
| 计算复杂度 | O(N) 或 O(N log N)(长序列可用快速算法) | O(N)(但无法并行) |
| 硬件适配 | 适合 GPU/TPU 大批量卷积运算 | 在 GPU 上效率不如卷积/SSM |
4. 应用差别
-
SSM
- 现代深度学习中多用于长序列建模:语言(Mamba)、音频(Hyena)、DNA 序列(Genomics)
- 特别适合输入很长且依赖分布广的任务
- 数学上可视为可学习的无限长卷积核
-
LSTM
- 经典时间序列和 NLP(在 Transformer 出现前)主力
- 常用于短到中等长度的依赖任务(机器翻译、语音识别、金融预测)
- 仍在小数据量、低延迟场景中表现很好
✅ 一句话总结:
- LSTM = “一步一步记笔记的秘书”,擅长短期和中期记忆,但速度慢。
- SSM = “会用数学公式一次性回忆整本书的工程师”,更适合长序列和大规模并行计算。
如果你愿意,我可以帮你画一张**“SSM vs LSTM 工作原理对比流程图”**,直观展示两者在信息流动上的差异,这样看会更清晰。你要我画吗?
5. 详细对比
3.1 计算效率
- SSM:通过离散化(卷积形式)或并行扫描算法,计算复杂度为 O(n)O(n)O(n),内存占用低。Mamba 等变体进一步优化了 GPU 并行计算,适合长序列(如百万 token)。
- LSTM:递归计算导致复杂度为 O(n⋅d2)O(n \cdot d^2)O(n⋅d2),其中 ddd 是隐状态维度。长序列会导致计算瓶颈,且难以并行化。
3.2 长序列建模
- SSM:选择性 SSM(如 Mamba)通过动态参数调整和线性复杂度,天然适合长序列建模,内存效率高。
- LSTM:通过遗忘门保留长期依赖,但递归计算和梯度传播限制了其处理超长序列的能力。
3.3 动态性
- SSM:选择性 SSM 显式地让 B,C,ΔB, C, \DeltaB,C,Δ 依赖输入,动态捕捉序列模式,表达能力更强。
- LSTM:通过门控机制(如遗忘门、输入门)间接实现动态记忆,但灵活性不如选择性 SSM。
3.4 训练与优化
- SSM:训练相对简单,Mamba 等模型通过硬件加速算法优化了前向和反向传播。
- LSTM:门控机制导致参数较多,训练时易出现梯度问题,需精心调参(如梯度裁剪)。
适用场景
- SSM:
- 适合需要高效处理长序列的任务,如长文档语言建模、时间序列预测(金融、传感器数据)、语音处理等。
- Mamba 等变体在性能上可媲美 Transformer,适用于现代深度学习任务。
- LSTM:
- 适用于传统序列建模任务,如早期 NLP(情感分析、序列标注)或短序列时间预测。
- 在资源受限或序列较短的场景中仍具竞争力。
3、并行扫描
好,这个问题其实是 SSM(状态空间模型)能支持“并行扫描” 的核心优势之一,和 LSTM 为什么不能并行 正好形成鲜明对比。
我先从数学原理说起,然后给你一个公式推导,再举一个具体数值例子,最后用类比帮你直观理解。
1. 原理:为什么能并行
假设我们有一个离散时间状态空间系统:
xt+1=Axt+Butx_{t+1} = A x_t + B u_t xt+1=Axt+But
yt=Cxt+Duty_t = C x_t + D u_t yt=Cxt+Dut
其中:
- xtx_txt 是隐藏状态(向量)
- utu_tut 是输入
- A,B,C,DA, B, C, DA,B,C,D 是固定矩阵(SSM 的核心假设)
1.1 并行化的关键
因为 AAA 是固定矩阵,所以:
-
经过 1 步:
x1=Ax0+Bu0x_1 = A x_0 + B u_0 x1=Ax0+Bu0
-
经过 2 步:
x2=A2x0+ABu0+Bu1x_2 = A^2 x_0 + A B u_0 + B u_1 x2=A2x0+ABu0+Bu1
-
经过 3 步:
x3=A3x0+A2Bu0+ABu1+Bu2x_3 = A^3 x_0 + A^2 B u_0 + A B u_1 + B u_2 x3=A3x0+A2Bu0+ABu1+Bu2
你会发现,这其实是一个卷积形式:
xt=Atx0+∑k=0t−1AkBut−1−kx_t = A^t x_0 + \sum_{k=0}^{t-1} A^k B u_{t-1-k} xt=Atx0+k=0∑t−1AkBut−1−k
这意味着:
- 所有时间步的计算只依赖矩阵幂 AkA^kAk
- 这些矩阵幂可以通过快速幂 + FFT 卷积一次性并行计算
- 不需要像 LSTM 那样“等前一步算完才能算下一步”
2. 与 LSTM 对比
-
LSTM:
ht=f(ht−1,xt)h_t = f(h_{t-1}, x_t) ht=f(ht−1,xt)
hth_tht 必须等 ht−1h_{t-1}ht−1 计算出来后才能继续 → 只能顺序计算。
-
SSM:
递推关系是线性+固定系数,矩阵幂运算可以分治并行 → 并行扫描(parallel scan)。
3. 并行扫描的具体数值例子
假设:
A=0.9,B=1,x0=0A = 0.9, \quad B = 1, \quad x_0 = 0 A=0.9,B=1,x0=0
输入序列:
u=[1,2,3,4]u = [1, 2, 3, 4] u=[1,2,3,4]
普通递推(像 LSTM 一样顺序算):
- x1=0.9⋅0+1⋅1=1x_1 = 0.9 \cdot 0 + 1 \cdot 1 = 1x1=0.9⋅0+1⋅1=1
- x2=0.9⋅1+1⋅2=2.9x_2 = 0.9 \cdot 1 + 1 \cdot 2 = 2.9x2=0.9⋅1+1⋅2=2.9
- x3=0.9⋅2.9+1⋅3=5.61x_3 = 0.9 \cdot 2.9 + 1 \cdot 3 = 5.61x3=0.9⋅2.9+1⋅3=5.61
- x4=0.9⋅5.61+1⋅4=9.049x_4 = 0.9 \cdot 5.61 + 1 \cdot 4 = 9.049x4=0.9⋅5.61+1⋅4=9.049
并行扫描做法:
-
先预计算 AkA^kAk:
A1=0.9A^1 = 0.9A1=0.9, A2=0.81A^2 = 0.81A2=0.81, A3=0.729A^3 = 0.729A3=0.729 -
把它当成卷积核:
kernel=[1,0.9,0.81,0.729]\text{kernel} = [1, 0.9, 0.81, 0.729] kernel=[1,0.9,0.81,0.729]
-
卷积 uuu 和 kernel:
x=[1,2.9,5.61,9.049]x = [1, 2.9, 5.61, 9.049] x=[1,2.9,5.61,9.049]
结果一模一样,但:
- 卷积可以用 FFT 一次性算完
- GPU 上可并行处理,时间复杂度从 O(N) → O(N log N)
4. 直观类比
- LSTM 就像“传纸条”:你要等前一个人写完并传给你,才能接着写 → 串行。
- SSM 并行扫描 就像“所有人都知道传纸条的规律”,大家只要知道公式就能同时算出自己这一步的结果 → 并行。
5. 在 Mamba 中的优化
- Mamba 使用 并行扫描(parallel scan)+ kernel fusion
- 把状态传播和输入投影合并到一次 GPU kernel 调用里 → 极大减少内存访问
- 因为是并行卷积,长序列(>100k token)推理速度比 Transformer 快 5-10 倍
如果你愿意,我可以帮你画一张并行扫描计算图,把 “顺序递推” 和 “并行卷积” 在 GPU 上的执行方式对比出来,看一眼就能明白为什么 SSM 能加速。
你要我画吗?这样会更直观。
我来帮你把 Mamba 支持并行扫描 的原理拆开讲清楚,并配上一个具体例子,这样你能一步一步看出来它跟传统 RNN(比如 LSTM)的差异在哪里。
1. 先理解“并行扫描”指什么
- 扫描 (scan) 指的是对序列数据按时间步依次累积状态的过程(又叫 prefix-scan 或者 prefix-sum 的广义形式)。
- 例如,在 RNN 或 LSTM 中,隐状态更新公式是这样的:
ht=f(ht−1,xt)h_t = f(h_{t-1}, x_t) ht=f(ht−1,xt)
这里 hth_tht 的计算依赖 上一个时间步的隐状态 ht−1h_{t-1}ht−1,所以必须按顺序一个一个算,这就是 串行扫描,不能并行。
- 并行扫描 意思是:即使状态更新公式中有时间依赖,也能用算法重写成 并行矩阵运算,一次性算出所有时间步的结果,而不是一个一个循环。
为什么 LSTM 不行
在 LSTM 里,状态更新依赖于非线性(sigmoid、tanh)后的前一步状态:
ct=ft⊙ct−1+it⊙gtc_t = f_t \odot c_{t-1} + i_t \odot g_t ct=ft⊙ct−1+it⊙gt
非线性和逐步依赖使得无法用矩阵一次性“跳过”中间时间步,所以没法并行。
2. Mamba 的关键:线性状态空间模型 (SSM) 的结构
Mamba 的核心是 SSM(State Space Model),其连续时间公式是:
h˙(t)=Ah(t)+Bx(t)y(t)=Ch(t)\dot{h}(t) = A h(t) + B x(t) \\ y(t) = C h(t) h˙(t)=Ah(t)+Bx(t)y(t)=Ch(t)
离散化后,得到类似:
ht=Aˉht−1+Bˉxth_t = \bar{A} h_{t-1} + \bar{B} x_t ht=Aˉht−1+Bˉxt
yt=Chty_t = C h_t yt=Cht
注意这里的 Aˉ,Bˉ,C\bar{A}, \bar{B}, CAˉ,Bˉ,C 都是固定矩阵(或者在 Mamba 里是输入依赖但仍然结构特殊的矩阵)。
这个公式只有线性运算(矩阵乘法和加法),没有 LSTM 那样的非线性依赖,所以可以用 矩阵幂 和 并行前缀和算法 来直接跳过中间状态。
并行扫描是怎么做到的
对于公式:
ht=Aht−1+bth_t = A h_{t-1} + b_t ht=Aht−1+bt
展开就是:
h1=Ah0+b1h_1 = A h_0 + b_1 h1=Ah0+b1
h2=Ah1+b2=A(Ah0+b1)+b2=A2h0+Ab1+b2h_2 = A h_1 + b_2 = A (A h_0 + b_1) + b_2 = A^2 h_0 + A b_1 + b_2 h2=Ah1+b2=A(Ah0+b1)+b2=A2h0+Ab1+b2
h3=A3h0+A2b1+Ab2+b3h_3 = A^3 h_0 + A^2 b_1 + A b_2 + b_3 h3=A3h0+A2b1+Ab2+b3
我们可以看到每个时间步的结果是:
- 前一状态乘以 AAA 的幂
- 加上之前所有输入的线性组合
由于这是纯线性形式,可以用前缀扫描算法(比如 parallel prefix-sum / Blelloch scan)在 O(log T) 步并行完成,而不是 O(T) 顺序循环。
按并行扫描(跳过中间步骤):
- 计算幂: A1,A2,A3,A4A^1, A^2, A^3, A^4A1,A2,A3,A4
- 前缀和公式:
ht=Ath0+∑k=1tAt−kbkh_t = A^t h_0 + \sum_{k=1}^t A^{t-k} b_k ht=Ath0+k=1∑tAt−kbk
- 具体小例子
假设我们有一个很短的序列:
- A=2A = 2A=2(标量,为了方便)
- 输入序列 b=[1,3,5,7]b = [1, 3, 5, 7]b=[1,3,5,7]
- 初始状态 h0=0h_0 = 0h0=0
按普通循环(串行扫描):
t=1: h1 = 2*h0 + 1 = 1
t=2: h2 = 2*h1 + 3 = 5
t=3: h3 = 2*h2 + 5 = 15
t=4: h4 = 2*h3 + 7 = 37
按并行扫描(跳过中间步骤):
- 计算幂: A1,A2,A3,A4A^1, A^2, A^3, A^4A1,A2,A3,A4
- 前缀和公式:
ht=Ath0+∑k=1tAt−kbkh_t = A^t h_0 + \sum_{k=1}^t A^{t-k} b_k ht=Ath0+k=1∑tAt−kbk
一次性矩阵化运算:
h1 = 2^1*0 + 2^0*1 = 1
h2 = 2^2*0 + 2^1*1 + 2^0*3 = 5
h3 = 2^3*0 + 2^2*1 + 2^1*3 + 2^0*5 = 15
h4 = 2^4*0 + 2^3*1 + 2^2*3 + 2^1*5 + 2^0*7 = 37
所有时间步的结果可以通过一次矩阵乘法批量算出,支持 GPU 并行。
4、Mamba系列
以下是关于 Mamba 系列模型的版本及其具体改进 的详细解析:
1. Mamba(原始版本)
-
最早在 2023 年由 Tri Dao 与 Albert Gu 提出,完整论文题为 “Mamba: Linear-Time Sequence Modeling with Selective State Spaces” (IBM, arXiv)。
-
核心架构:基于 Selective SSM(S6),其关键创新包括:
- 选择性参数机制:将 SSM 的参数(如 Δₜ、Bₜ、Cₜ)动态依赖于当前输入,从而能够“选择性聚焦或忽略”不同部分的输入历史,类似 Attention 的功能 (IBM, arXiv)。
- 硬件感知并行扫描算法:利用 GPU 的并行扫描、内核融合(kernel fusion)等技巧,提高推理效率,避免显存瓶颈,能实现比传统卷积型 SSM 快约 3× 的推理速度,并具有线性时间复杂度 (arXiv, 维基百科)。
- 模型架构简化:融合 SSM 与 MLP,形成统一的 Mamba block,替代传统 Transformer 中的 Attention + MLP 结构 (arXiv, 维基百科)。
- 在长序列(百万级 Token)任务中,表现优异,在多模态任务(语言、音频、基因组建模)上具有强泛化能力 (arXiv, The Gradient)。
2. Mamba-2(基于 SSD 的新版)
-
2024 年发布的后续工作,《Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality》提出了 Mamba-2(基于 SSD 框架) (arXiv, 维基百科)。
-
主要改进点包括:
-
状态空间对偶性(SSD)设计:建立 SSM 与 Attention 的数学对等(使用结构化半可分矩阵 semiseparable matrices),统一两者算法,提升硬件并行效率 (维基百科)。
-
结构优化:
- 参数前置:将 A、B、C 等矩阵的计算移至模块初始化阶段,减少每步依赖计算延迟;
- 引入 Grouped-Value Attention(GVA) 结构,减少内存占用,同时支持张量并行;
- 添加归一化层(借鉴 NormFormer),提升训练稳定性;
- 支持混合架构:部分 SSD 层替换为 Attention 层能进一步提升性能 (维基百科)。
-
效率与性能提升:
- 在保持线性复杂度的同时,推理速度提升达 2–8 倍;
- 支持大规模分布式训练(如 Megatron 风格张量并行);
- 在 Chinchilla 缩放定律下,在困惑度和训练效率上优于原 Mamba 和 Transformer++,尤其在长序列任务上表现更强 (维基百科)。
-
3. 其他 Mamba 变体与应用案例
-
Bi-Mamba(1 位量化模型)
— 引入 1-bit 量化技术,显著降低内存与能耗,同时保持与 FP16/BF16 Mamba 相近的性能,适用于低资源部署场景 (OpenReview)。 -
其他领域改造与融合模型(部分来自中文维基):
- MambaByte:以原始字节为处理单位的 token-free 模型,让预处理更加语言无关 (维基百科)。
- MoE-Mamba:将 Mixture-of-Experts 与 Mamba 结合,该模型训练时间减少约 2.2 倍,同时保留性能 (维基百科)。
- Vision Mamba(Vim):用于视觉任务,采用双向 SSM,减少注意力带来的计算开销,在 ImageNet、COCO、ADE20k 等任务上表现优异 (维基百科)。
- Jamba:AI21 Labs 打造的 SSM-Transformer 混合模型,拥有 520 亿参数和 256k token 上下文窗口 (维基百科)。
总结一览表
| 版本 / 变体 | 核心改进 | 优势 |
|---|---|---|
| Mamba-1 | 动态选择性参数 + 并行扫描 + 架构简化 | 高效推理、长序列处理 |
| Mamba-2 (SSD) | SSD 数学框架 + GVA + 参数前置 + 归一化 | 推理更快(2–8×)、更高效训练 |
| Bi-Mamba | 1-bit 量化 | 极低内存与能耗 |
| 其他变体 | Token-free、MoE、视觉版本、混合模型等 | 针对特定任务优化 |
如你对任意版本或变体(如 Jamba、MoE-Mamba、Vision Mamba 等)更感兴趣,我也可以继续深入聊,或者帮你找具体论文资源与代码实现,随时欢迎继续提问!
你提到“时间序列 Mamba 版本及具体改进”,我理解你关注的是 Mamba 在时序建模(Time Series Modeling/Forecasting)领域的不同版本或变体及其改进。以下是按版本或衍生模型分类的梳理与对比:
时间系列Mamba
1. S-Mamba(Simple-Mamba)
- 提出时间:2024 年 3 月。
- 特点:基于 Mamba 架构,采用双向 Mamba 层提取多变量间的相关性,再用 FFN 捕捉时间依赖,最后线性预测输出。
- 优势:具备近线性复杂度,显著降低计算资源消耗(GPU 内存、训练时间),在 13 个公开数据集上展现领先性能 (arXiv)。
2. MambaTS
-
提出时间:2024 年 5 月(ICLR 2025 投稿)。
-
主要改进:引入四项关键机制:
- Variable-Aware Scan (VAST):在训练时自动发现变量间关系,并在推理中优化扫描顺序。
- Temporal Mamba Block (TMB):去除原 Mamba 中的因果卷积,更适用于多变量时间序列。
- Selective-参数 Dropout:缓解过拟合。
- 实现在多个数据集上创下 SOTA 性能 (arXiv, OpenReview)。
3. Bi-Mamba+
- 提出时间:2024 年 4 月。
- 创新点:在 Mamba Block 内添加“遗忘门”,融合前向与后向信息,增强历史信息建模能力;并引入特定的数据感知机制,以处理多变量数据结构差异 (arXiv)。
4. ms-Mamba(Multi-scale Mamba)
- 提出时间:2025 年 4 月。
- 改进方向:通过不同采样率的多尺度 Mamba Block 提升对多时长变化信息的捕捉能力,效果优于传统 Transformer 及 Mamba 变体 (arXiv)。
5. SOR-Mamba(Sequential Order-Robust Mamba)
- 提出时间:2024 年 9 月(ICLR 2025 投稿)。
- 主要改进:针对时间序列中“通道(变量)无序”的问题,设计了顺序无偏正则化,增强模型对通道排列的鲁棒性;同时提出通道相关性预训练任务 (OpenReview)。
6. Attention Mamba
- 提出时间:2025 年 4 月。
- 亮点:添加一个 Adaptive Pooling Block 加速注意力计算,扩展感受野,同时整合了双向 Mamba 以更有效捕捉长短期特征,提升非线性依赖建模能力 (arXiv)。
7. SpectroMamba(包括 BV-Mamba)
- 提出时间:近期(2025 年)。
- 特征:结合时域与频域信息,设计了 Spectral Attention Module(SAM),以及用于跨变量建模的 Bidirectional Variable Mamba (BV-Mamba),构成 SpectroMamba 框架,显著提升多变量 TSF 性能 (SpringerLink)。
8. Mamba-ProbTSF(Uncertainty Quantification)
- 提出时间:最近。
- 创新点:采用双网络架构,一份输出预测值,另一份预测不确定性(方差),实现时间序列预测的概率性输出,提高预测可信度 (ResearchGate)。
总览对比表
| 版本 / 变体 | 核心改进 | 应用优势 |
|---|---|---|
| S-Mamba | 简化结构 + 双向 Mamba | 高效、低资源,领先表现 |
| MambaTS | VAST + TMB + Dropout | 全局依赖建模、SOTA 性能 |
| Bi-Mamba+ | 引入遗忘门 + 前后双向融合 | 更强历史信息保持能力 |
| ms-Mamba | 多尺度处理 | 捕捉不同变化速率的时序信息 |
| SOR-Mamba | 通道顺序鲁棒性增强 | 更适合通道无序的多变量数据 |
| Attention Mamba | 加速注意力 + 更长感受野 | 更强非线性与长依赖建模能力 |
| SpectroMamba | 时频联合 + BV-Mamba | 多变量建模更全面、更优性能 |
| Mamba-ProbTSF | 不确定性估计 | 提供预测可信度与区间判断 |
如果你希望深入了解某个版本的架构细节、实验结果或代码使用方式,欢迎继续告诉我,我可以进一步展开说明。
5、Mamba2
概览(一句话)
Mamba-2 的核心是 Structured State-Space Duality (SSD):把选择性状态空间模型(SSM)写成一个三角的 semiseparable 矩阵,在标量-单位(scalar-identity)情形下该矩阵可以分解成一个结构化 mask LLL 与低秩因子 CB⊤C B^\topCB⊤ 的逐元素乘积,从而在“线性递推(SSM)”和“注意力/张量收缩(attention)”两种算法次序之间切换以获得效率与并行度的折中。(Tri Dao, arXiv)
关键符号与起点(约定)
- 序列长度 TTT。
- 输入序列 X=[x0,…,xT−1]X = [x_0, \dots, x_{T-1}]X=[x0,…,xT−1],每个 xt∈RPx_t\in\mathbb{R}^Pxt∈RP。
- 隐状态维度(SSM 中)为 NNN。 用下标 t,s,i,jt,s,i,jt,s,i,j 表示时间索引。
- 选择性 SSM(Selective SSM)一般写作(离散形式)
ht=Atht−1+Btxt,yt=Ct⊤ht(或 yt=Ct⊤ht+Dtxt).\begin{aligned} h_t &= A_t\, h_{t-1} + B_t\, x_t,\\ y_t &= C_t^\top h_t \quad (\text{或 } y_t = C_t^\top h_t + D_t x_t). \end{aligned} htyt=Atht−1+Btxt,=Ct⊤ht(或 yt=Ct⊤ht+Dtxt).
这是 Mamba / Mamba-2 的基础 recurrence。(Tri Dao)
选择性 SSM 的数学基础
Mamba-2 基于选择性 SSM 的离散形式,公式如下:
ht=Atht−1+Btxt(1a)h_t = A_t h_{t-1} + B_t x_t \tag{1a} ht=Atht−1+Btxt(1a)
yt=Ct⊤ht(1b)y_t = C_t^\top h_t \tag{1b} yt=Ct⊤ht(1b)
- ht∈RNh_t \in \mathbb{R}^Nht∈RN: 隐状态(状态维度 N≥64N \geq 64N≥64)。
- xt,yt∈RPx_t, y_t \in \mathbb{R}^Pxt,yt∈RP: 输入/输出(头维度 P≥64P \geq 64P≥64)。
- 参数:At∈RN×NA_t \in \mathbb{R}^{N \times N}At∈RN×N, Bt∈RN×PB_t \in \mathbb{R}^{N \times P}Bt∈RN×P, Ct∈RN×PC_t \in \mathbb{R}^{N \times P}Ct∈RN×P,在 SSD 中 At=atIA_t = a_t IAt=atI(at∈[0,1]a_t \in [0,1]at∈[0,1] 为输入依赖标量)。
- 序列形式:Y(T,P)=SSM(A(T),B(T,N),C(T,N))(X(T,P))Y^{(T,P)} = \mathsf{SSM}(A^{(T)}, B^{(T,N)}, C^{(T,N)})(X^{(T,P)})Y(T,P)=SSM(A(T),B(T,N),C(T,N))(X(T,P))。
矩阵变换表示:
将 SSM 展开为矩阵乘法 y=Mxy = M xy=Mx,其中 M∈RT×TM \in \mathbb{R}^{T \times T}M∈RT×T 是下三角矩阵:
Mji=Cj⊤Aj:i+1×Bi=Cj⊤(Aj⋯Ai+1)Bi(2)M_{ji} = C_j^\top A_{j:i+1}^\times B_i = C_j^\top (A_j \cdots A_{i+1}) B_i \tag{2} Mji=Cj⊤Aj:i+1×Bi=Cj⊤(Aj⋯Ai+1)Bi(2)
- Aj:i+1×A_{j:i+1}^\timesAj:i+1×: 矩阵累乘。
- 完整矩阵 MMM:
M=[C0⊤B00⋯0C1⊤A1B0C1⊤B1⋱⋮⋮⋮⋱0CT−1⊤AT−1⋯A1B0CT−1⊤AT−1⋯A2B1⋯CT−1⊤BT−1](3)M = \begin{bmatrix} C_0^\top B_0 & 0 & \cdots & 0 \\ C_1^\top A_1 B_0 & C_1^\top B_1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & 0 \\ C_{T-1}^\top A_{T-1} \cdots A_1 B_0 & C_{T-1}^\top A_{T-1} \cdots A_2 B_1 & \cdots & C_{T-1}^\top B_{T-1} \end{bmatrix} \tag{3} M=C0⊤B0C1⊤A1B0⋮CT−1⊤AT−1⋯A1B00C1⊤B1⋮CT−1⊤AT−1⋯A2B1⋯⋱⋱⋯0⋮0CT−1⊤BT−1(3)
这是一个 NNN- 半可分矩阵(semiseparable matrix),即所有下三角子矩阵的秩至多为 NNN。
标量特例(N=1):
简化为:
ht=atht−1+bt(4)h_t = a_t h_{t-1} + b_t \tag{4} ht=atht−1+bt(4)
对应矩阵 MMM 为累积乘加(cumprodsum):
M=[10⋯a11⋱a2a1a21⋮⋮⋱⋱](5)M = \begin{bmatrix} 1 & 0 & \cdots \\ a_1 & 1 & \ddots \\ a_2 a_1 & a_2 & 1 \\ \vdots & \vdots & \ddots & \ddots \end{bmatrix} \tag{5} M=1a1a2a1⋮01a2⋮⋯⋱1⋱⋱(5)
把 SSM 展成矩阵 —— semiseparable 表示(关键公式)
把上面的递推完全展开(unroll),可以写成一个对输入做一次矩阵乘法的形式 Y=MXY = M XY=MX,其中 MMM 是下三角的 semiseparable 矩阵,且其条目为:
Mij={Ci⊤Ai:j×Bj,i≥j,0,i<j,M_{ij} \;=\; \begin{cases} C_i^\top \, A_{i:j}^\times\, B_j, & i\ge j,\\[4pt] 0, & i<j, \end{cases} Mij={Ci⊤Ai:j×Bj,0,i≥j,i<j,
其中约定
Ai:j×:=AiAi−1⋯Aj+1A_{i:j}^\times := A_i A_{i-1}\cdots A_{j+1} Ai:j×:=AiAi−1⋯Aj+1
(注意索引顺序 — 这是把递推展开后得到的乘积)。这就是所谓的**矩阵变换(matrix transformation)**或 token-mixer 表示。(Tri Dao)
标量-单位(scalar-identity)情形 — SSD 的核心代数等价
若每个 AtA_tAt 为标量乘单位矩阵,写成 At=atINA_t = a_t I_NAt=atIN(scalar-identity),那么上式中矩阵乘积可把标量因子提出:
Ci⊤Ai:j×Bj=(∏k=j+1iak)⋅(Ci⊤Bj).C_i^\top A_{i:j}^\times B_j = \Big(\prod_{k=j+1}^{i} a_k\Big)\cdot (C_i^\top B_j). Ci⊤Ai:j×Bj=(k=j+1∏iak)⋅(Ci⊤Bj).
定义
- Lij:=∏k=j+1iakL_{ij} := \prod_{k=j+1}^{i} a_kLij:=∏k=j+1iak(当 i≥ji\ge ji≥j;否则 Lij=0L_{ij}=0Lij=0),得到一个特定结构的下三角矩阵(文中称为 1-semiseparable 或 1-SS 矩阵),
- 以及把 {Ci},{Bj}\{C_i\},\{B_j\}{Ci},{Bj} 看作行/列因子,则有矩阵级别的注意力样分解:
M=L∘(CB⊤),M \;=\; L \circ (C B^\top), M=L∘(CB⊤),
这里 ∘\circ∘ 表示逐元素(Hadamard)乘积。等价地,单步条目写作
yt=∑s≤tLts(Ct⊤Bs)xs.y_t \;=\; \sum_{s\le t} L_{t s}\, (C_t^\top B_s)\, x_s. yt=s≤t∑Lts(Ct⊤Bs)xs.
这就是 SSD 的代数核心:SSM 的 kernel(semiseparable 矩阵)可以表示为结构化 mask LLL 与低秩外积 CB⊤C B^\topCB⊤ 的逐元素乘积。(Tri Dao)
两种计算次序(dual algorithms):线性形式 vs 二次形式(及其等价)
从上面的 M=L∘(CB⊤)M = L\circ(CB^\top)M=L∘(CB⊤) 出发,有两种自然的计算次序(也就是 SSD 的“线性-二次对偶”):
-
线性(SSM 递推)形式 — 逐步递推(时间因果):
令zt=Atzt−1+Btxt,z−1=0,z_t = A_t z_{t-1} + B_t x_t,\qquad z_{-1}=0, zt=Atzt−1+Btxt,z−1=0,
则
yt=Ct⊤zt.y_t = C_t^\top z_t. yt=Ct⊤zt.
这是原始 SSM 的 O(T⋅N⋅PT\cdot N\cdot PT⋅N⋅P) 逐步算法(对每个时间步做矩阵-向量递推),对序列长度是线性的。(Tri Dao)
-
二次 / 注意力 样(materialize)形式 — 先构造(或以张量收缩得到)类似 QK⊤QK^\topQK⊤ 的矩阵,再乘以 VVV:
把 Qt:=CtQ_t := C_tQt:=Ct, Ks:=BsK_s := B_sKs:=Bs, Vs:=xsV_s := x_sVs:=xs 看作三组向量,则Y=(L∘(QK⊤))V.Y = (L\circ (QK^\top))\, V. Y=(L∘(QK⊤))V.
直接 materialize L∘(QK⊤)L\circ(QK^\top)L∘(QK⊤) 并做矩阵乘法是二次复杂度 O(T2)O(T^2)O(T2) 的方法,但在实现上可以通过合适的张量变换(例如先计算 K⊤VK^\top VK⊤V 或在块上并行)利用高速 matmul 原语更高效地利用硬件(tensor cores)。(Tri Dao, Goomba Lab)
要点:当 LLL 有特殊结构时(例如因子化为一系列标量积,或块 Toeplitz 等),对 LLL 的乘法 y=Lxy=Lxy=Lx 可以用累加/scan(cumsum)或递推在 O(T) 时间内完成;而当 N(状态通道)>>1 且能利用大矩阵乘法时,把计算按块转成 matmul(quadratic-on-chunk)再把块间状态用递推传递,往往能在实际 GPU 上更快(Mamba-2 的 hybrid/块算法思想)。(Tri Dao, Goomba Lab)
Mamba-2 在算法/实现层面的优化(简要公式化说明)
Mamba-2 的工程关键在于把上面两种次序的优点组合起来,使实现既能用 matmul(tensor-core)高吞吐,又能保持序列线性/因果性的精确性。核心手段包括:
- head-wise 参数共享 / 批量化产生 A,B,CA,B,CA,B,C:把每个 head 的 SSM 参数并行化为张量,使得很多小矩乘能合并成几个大 matmul(利用高效率的矩阵乘法)。(Tri Dao, Goomba Lab)
- 块分解(chunk/block decomposition):把整个 MMM 划分为若干块,对每个块内部用“二次/块 matmul”计算(materialize 局部的 CB⊤C B^\topCB⊤ 并乘以局部的 LLL),而块之间只传递压缩的状态(用递推),从而在复杂度与硬件利用之间取得折中。数学上等价于对 semiseparable 矩阵做块分解然后交替使用 matmul 与 scan。(Goomba Lab)
- 混合(Hybrid)架构:在网络层级上允许部分层使用 Mamba-2(SSD 层)而部分层使用常规 attention(以提高局部/全局交互能力),这在实证上常被采用。(arXiv)
把上面内容串成一个紧凑推导(供 copy-paste 的主要公式)
(1)SSM 原始递推:
ht=Atht−1+Btxt,yt=Ct⊤ht.h_t = A_t h_{t-1} + B_t x_t,\quad y_t = C_t^\top h_t. ht=Atht−1+Btxt,yt=Ct⊤ht.
(2)矩阵化(semiseparable):
Y=MX,Mij={Ci⊤Ai:j×Bj,i≥j,0,i<j,Ai:j×≜AiAi−1⋯Aj+1.Y = M X,\qquad M_{ij} = \begin{cases} C_i^\top A_{i:j}^\times B_j,& i\ge j,\\[2pt] 0,& i<j, \end{cases} \quad A_{i:j}^\times \triangleq A_i A_{i-1}\cdots A_{j+1}. Y=MX,Mij={Ci⊤Ai:j×Bj,0,i≥j,i<j,Ai:j×≜AiAi−1⋯Aj+1.
(3)标量-单位情形(SSD 型):
At=atI⇒Mij=(∏k=j+1iak)(Ci⊤Bj),A_t = a_t I \;\Rightarrow\; M_{ij} = \Big(\prod_{k=j+1}^{i} a_k\Big) (C_i^\top B_j), At=atI⇒Mij=(k=j+1∏iak)(Ci⊤Bj),
即
M=L∘(CB⊤),Lij=∏k=j+1iak(i≥j).M = L\circ (C B^\top),\quad L_{ij}=\prod_{k=j+1}^{i} a_k\ (i\ge j). M=L∘(CB⊤),Lij=k=j+1∏iak (i≥j).
(4)两种计算次序:
线性(递推):zt=Atzt−1+Btxt,yt=Ct⊤zt.\textbf{线性(递推):}\quad z_t=A_t z_{t-1} + B_t x_t,\quad y_t=C_t^\top z_t. 线性(递推):zt=Atzt−1+Btxt,yt=Ct⊤zt.
二次(张量收缩):Y=(L∘(CB⊤))X,\textbf{二次(张量收缩):}\quad Y=(L\circ (C B^\top))\,X, 二次(张量收缩):Y=(L∘(CB⊤))X,
两者数值等价,但在实现复杂度/并行度上不同。(Tri Dao, Goomba Lab)
参考(进一步读物)
- Tri Dao 系列文章(State Space Duality / Mamba-2 parts I/II/III)— 最详尽的数学与算法推导(本文的主要公式与证明来源)。(Tri Dao, Goomba Lab)
- “Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality”(arXiv)— 形式化框架与定理。(arXiv)
- 原始 Mamba 论文(Mamba: Linear-Time Sequence Modeling with Selective State Spaces)—— 背景与最初的 SSM-based 架构。(arXiv)
- 大规模比较实验(Empirical Study of Mamba-based Language Models)—— Mamba-2 / Hybrid 在实证上的表现对比。(arXiv)
如果你想,我可以:
- 把上面的推导写成一份 LaTeX 笔记(带编号定理与证明细节),或
- 给出 Mamba-2 Part III 中块算法的伪代码并标注 FLOPs 与内存开销,或
- 针对你关心的一个具体点(例如如何把 L∘(CB⊤)L\circ(CB^\top)L∘(CB⊤) 在 GPU 上按块实现以利用 tensor cores)做更深一步的公式与实现说明。
你想先看哪一部分?
Mamba-2 原理教程:详细公式说明
Mamba-2 是 Mamba 序列建模架构的改进版本,基于**结构化状态空间二元性(Structured State Space Duality, SSD)**框架。该框架揭示了状态空间模型(State Space Models, SSMs)和注意力机制的数学等价性,通过简化参数结构(如标量身份矩阵)和高效矩阵乘法算法,提升了模型的训练速度(2-8 倍)和容量,同时保持线性复杂度对长序列的处理能力。Mamba-2 的核心创新在于将 SSM 表示为因果线性注意力(无 softmax),并通过块分解和分块计算优化硬件利用率。下面是详细原理教程,重点强调数学公式、推导和计算细节。
1. 背景与核心创新
- 从 Mamba-1 到 Mamba-2:
- Mamba-1 使用选择性 SSM,参数 At,Bt,CtA_t, B_t, C_tAt,Bt,Ct 依赖输入,但 AtA_tAt 为对角矩阵,状态维度 NNN 较小(通常 16),依赖并行关联扫描。
- Mamba-2 通过 SSD 框架简化 At=atIA_t = a_t IAt=atI(标量乘身份矩阵),允许更大 NNN(64-256)和头维度 PPP(如 64),并将计算转向矩阵乘法(matmul),利用 GPU 张量核心。
- SSD 框架:
- 独立层:一个可插入深度网络的 SSD 层,类似于注意力或 SSM。
- 通用框架:统一 SSM 和注意力,通过半可分矩阵(semiseparable matrices)等价。
- 高效算法:基于块分解的矩阵乘法,复杂度从 O(T2)O(T^2)O(T2)(二次)到 O(TN2)O(T N^2)O(TN2)(线性优化)。
2. 选择性 SSM 的数学基础
Mamba-2 基于选择性 SSM 的离散形式,公式如下:
ht=Atht−1+Btxt(1a)h_t = A_t h_{t-1} + B_t x_t \tag{1a} ht=Atht−1+Btxt(1a)
yt=Ct⊤ht(1b)y_t = C_t^\top h_t \tag{1b} yt=Ct⊤ht(1b)
- ht∈RNh_t \in \mathbb{R}^Nht∈RN: 隐状态(状态维度 N≥64N \geq 64N≥64)。
- xt,yt∈RPx_t, y_t \in \mathbb{R}^Pxt,yt∈RP: 输入/输出(头维度 P≥64P \geq 64P≥64)。
- 参数:At∈RN×NA_t \in \mathbb{R}^{N \times N}At∈RN×N, Bt∈RN×PB_t \in \mathbb{R}^{N \times P}Bt∈RN×P, Ct∈RN×PC_t \in \mathbb{R}^{N \times P}Ct∈RN×P,在 SSD 中 At=atIA_t = a_t IAt=atI(at∈[0,1]a_t \in [0,1]at∈[0,1] 为输入依赖标量)。
- 序列形式:Y(T,P)=SSM(A(T),B(T,N),C(T,N))(X(T,P))Y^{(T,P)} = \mathsf{SSM}(A^{(T)}, B^{(T,N)}, C^{(T,N)})(X^{(T,P)})Y(T,P)=SSM(A(T),B(T,N),C(T,N))(X(T,P))。
矩阵变换表示:
将 SSM 展开为矩阵乘法 y=Mxy = M xy=Mx,其中 M∈RT×TM \in \mathbb{R}^{T \times T}M∈RT×T 是下三角矩阵:
Mji=Cj⊤Aj:i+1×Bi=Cj⊤(Aj⋯Ai+1)Bi(2)M_{ji} = C_j^\top A_{j:i+1}^\times B_i = C_j^\top (A_j \cdots A_{i+1}) B_i \tag{2} Mji=Cj⊤Aj:i+1×Bi=Cj⊤(Aj⋯Ai+1)Bi(2)
- Aj:i+1×A_{j:i+1}^\timesAj:i+1×: 矩阵累乘。
- 完整矩阵 MMM:
M=[C0⊤B00⋯0C1⊤A1B0C1⊤B1⋱⋮⋮⋮⋱0CT−1⊤AT−1⋯A1B0CT−1⊤AT−1⋯A2B1⋯CT−1⊤BT−1](3)M = \begin{bmatrix} C_0^\top B_0 & 0 & \cdots & 0 \\ C_1^\top A_1 B_0 & C_1^\top B_1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & 0 \\ C_{T-1}^\top A_{T-1} \cdots A_1 B_0 & C_{T-1}^\top A_{T-1} \cdots A_2 B_1 & \cdots & C_{T-1}^\top B_{T-1} \end{bmatrix} \tag{3} M=C0⊤B0C1⊤A1B0⋮CT−1⊤AT−1⋯A1B00C1⊤B1⋮CT−1⊤AT−1⋯A2B1⋯⋱⋱⋯0⋮0CT−1⊤BT−1(3)
这是一个 NNN- 半可分矩阵(semiseparable matrix),即所有下三角子矩阵的秩至多为 NNN。
标量特例(N=1):
简化为:
ht=atht−1+bt(4)h_t = a_t h_{t-1} + b_t \tag{4} ht=atht−1+bt(4)
对应矩阵 MMM 为累积乘加(cumprodsum):
M=[10⋯a11⋱a2a1a21⋮⋮⋱⋱](5)M = \begin{bmatrix} 1 & 0 & \cdots \\ a_1 & 1 & \ddots \\ a_2 a_1 & a_2 & 1 \\ \vdots & \vdots & \ddots & \ddots \end{bmatrix} \tag{5} M=1a1a2a1⋮01a2⋮⋯⋱1⋱⋱(5)
3. 状态空间二元性(SSD):与注意力的等价性
SSD 揭示 SSM 和线性注意力的二元性:两者计算相同函数,但通过不同路径。
二元形式:
- SSM 形式(线性/递归):通过递归计算 hth_tht,复杂度 O(TN)O(T N)O(TN)。
- 注意力形式(二次):M=L∘(CB⊤)M = L \circ (C B^\top)M=L∘(CB⊤),其中 LLL 是下三角掩码矩阵:
Lij={ai:j×=ai⋯aj+1i≥j0i<j(6)L_{ij} = \begin{cases} a_{i:j}^\times = a_i \cdots a_{j+1} & i \geq j \\ 0 & i < j \end{cases} \tag{6} Lij={ai:j×=ai⋯aj+10i≥ji<j(6) - 然后 Y=MX=(L∘CB⊤)XY = M X = (L \circ C B^\top) XY=MX=(L∘CB⊤)X。
结构化掩码注意力(Structured Masked Attention, SMA):
将二元性泛化为四维张量收缩:
Y=contract(TN,SN,SP,TS→TP)(Q,K,V,L)(7)Y = \mathsf{contract}(TN, SN, SP, TS \to TP)(Q, K, V, L) \tag{7} Y=contract(TN,SN,SP,TS→TP)(Q,K,V,L)(7)
- 二次形式(注意力式):
G=contract(TN,SN→TS)(Q,K)(8a)G = \mathsf{contract}(TN, SN \to TS)(Q, K) \tag{8a} G=contract(TN,SN→TS)(Q,K)(8a)
M=contract(TS,TS→TS)(G,L)(8b)M = \mathsf{contract}(TS, TS \to TS)(G, L) \tag{8b} M=contract(TS,TS→TS)(G,L)(8b)
Y=contract(TS,SP→TP)(M,V)(8c)Y = \mathsf{contract}(TS, SP \to TP)(M, V) \tag{8c} Y=contract(TS,SP→TP)(M,V)(8c)
- 与 Transformer 注意力区别:无 softmax,使用输入依赖掩码 LLL 提供相对位置编码。
推导:
从 SSM 矩阵 Mji=Cj⊤Aj:i+1×BiM_{ji} = C_j^\top A_{j:i+1}^\times B_iMji=Cj⊤Aj:i+1×Bi 出发,当 At=atIA_t = a_t IAt=atI 时,Aj:i+1×=aj:i+1×IA_{j:i+1}^\times = a_{j:i+1}^\times IAj:i+1×=aj:i+1×I,于是 Mji=aj:i+1×(Cj⊤Bi)M_{ji} = a_{j:i+1}^\times (C_j^\top B_i)Mji=aj:i+1×(Cj⊤Bi),即 M=L∘(CB⊤)M = L \circ (C B^\top)M=L∘(CB⊤)。这证明 SSM 等价于带结构化掩码的线性注意力。
4. 高效算法与优化
Mamba-2 替换 Mamba-1 的并行扫描为基于 matmul 的 SSD 算法,通过块分解实现高效计算。
块矩阵分解(Block Decomposition):
将序列分为大小 QQQ 的块,矩阵 MMM 分解为对角块(橙色)和非对角块(绿色/蓝色):
- 对角块:小半可分矩阵,使用二次形式计算。
- 非对角块:低秩,使用批量 matmul 计算。
- 剩余项(黄色):1- 半可分矩阵,等价于 SSM 扫描。
分块算法(Chunkwise Algorithm):
将序列分成 T/QT/QT/Q 个块,步骤如下:
- 块内输出:假设初始状态 0,计算每个块的局部输出(使用二次形式)。
- 块状态:计算每个块的最终状态(假设初始状态 0)。
- 状态传递:在块最终状态上计算递归(并行或顺序扫描),得到每个块的真实初始状态。复杂度:O((T/Q)N)O((T/Q) N)O((T/Q)N)。
- 输出调整:使用真实初始状态计算输出贡献。
数值稳定性:段和(Segsum):
为避免累乘不稳定(小 ata_tat 导致下溢),在对数域计算:
ai:j×=exp((loga)i:T+−(loga)j:T+)(9)a_{i:j}^\times = \exp\left( (\log a)_{i:T}^+ - (\log a)_{j:T}^+ \right) \tag{9} ai:j×=exp((loga)i:T+−(loga)j:T+)(9)
- (loga)+(\log a)^+(loga)+: 累加(cumsum)。
- 使用 segsum 实现差异。
时间复杂度:
- 整体:O(TN2)O(T N^2)O(TN2) FLOPs(matmul 主导),并行深度 O(logT)O(\log T)O(logT)。
- 与 Mamba-1 比较:更快于大 NNN,支持张量并行(每层仅 1 次 all-reduce)。
5. Mamba-2 架构与对比
Mamba-2 模块:输入投影生成 A,B,CA, B, CA,B,C,SSD 核心计算,输出投影。支持混合(如 6 注意力 + 58 SSD 层)。
| 特性 | Mamba-1 | Mamba-2 | Transformer |
|---|---|---|---|
| A 结构 | 对角 | 标量身份 | 无 |
| 复杂度 | O(T N) 扫描 | O(T N^2) matmul | O(T^2 D) |
| N/P | N=16, P=1 | N=64-256, P=64 | 多头 |
| 速度 | 中等 | 2-8x 快 | 高但二次内存 |
6. 总结
Mamba-2 通过 SSD 二元性统一 SSM 和注意力,实现高效序列建模。其核心公式强调半可分矩阵和掩码注意力等价,算法优化聚焦 matmul 和块分解,适合长序列任务。如果你需要代码实现或特定推导扩展,请提供细节!
6、Mamba-2中n和p,和注意力机制对应关系
Mamba-2原理,其中n和p,和注意力机制对应关系,注意头的数量和维度关系怎么设置
注意:是一种维度对应关系
我给你详细解释一下 Mamba-2 里的 nnn 和 ppp,以及它们和注意力机制里的 dkd_kdk、dvd_vdv 的对应关系。
1. Mamba-2 中的 nnn 和 ppp
在 Mamba/Mamba-2 的公式里:
ht∈Rn,xt∈Rph_t \in \mathbb{R}^n,\quad x_t \in \mathbb{R}^p ht∈Rn,xt∈Rp
-
nnn → 状态维度(state dimension)
- 相当于 SSM 中隐藏状态 hth_tht 的长度。
- 决定了模型的记忆容量,影响可以建模的时间依赖长度。
- 在 Mamba-2 中,nnn 可以是几十到几百(比如 64、256),比 Mamba-1 的 16 要大很多。
-
ppp → 输入/输出通道数(input channel dimension)
- 相当于每个 token 输入 xtx_txt 的特征数。
- 在 NLP 场景下通常就是模型 embedding dim(比如 768, 1024)。
- 在公式 Bt∈Rn×pB_t \in \mathbb{R}^{n \times p}Bt∈Rn×p、Ct∈Rn×pC_t \in \mathbb{R}^{n \times p}Ct∈Rn×p 里,ppp 是列数。
公式:
ht∈Rn,xt∈Rph_t \in \mathbb{R}^n,\quad x_t \in \mathbb{R}^p ht∈Rn,xt∈Rp
ht=atht−1+Btxt,yt=Ct⊤hth_t = a_t\, h_{t-1} + B_t x_t,\quad y_t = C_t^\top h_t ht=atht−1+Btxt,yt=Ct⊤ht
其中:
- Bt∈Rn×pB_t \in \mathbb{R}^{n\times p}Bt∈Rn×p 把 ppp-dim 输入映射到 nnn-dim 状态
- Ct∈Rn×pC_t \in \mathbb{R}^{n\times p}Ct∈Rn×p 把 nnn-dim 状态读出到 ppp-dim 输出。
2. 对应到注意力机制
在标准多头注意力(Multi-Head Attention)中:
- dkd_kdk → key/query 向量维度
- dvd_vdv → value 向量维度
- dmodeld_{\text{model}}dmodel → 每个 token 的 embedding 维度(相当于 Mamba 里的 ppp)
Mamba-2 的对应关系可以这样类比:
| 注意力机制 | Mamba-2 对应量 | 含义 |
|---|---|---|
| dmodeld_{\text{model}}dmodel | ppp | token 输入/输出维度 |
| dkd_kdk | nnn | 状态空间维度,类似 key 的隐空间 |
| dvd_vdv | ppp | value 空间维度,与输入输出相同 |
| Q, K 交互 | Ct,BsC_t, B_sCt,Bs 交互 | 计算 Ct⊤BsC_t^\top B_sCt⊤Bs 类似 QKᵀ |
| 注意力 mask | LtsL_{ts}Lts | 来自 SSM 的递推掩码 |
对应到多头注意力(MHA)
在标准多头注意力(Multi-Head Attention)中:
- dmodeld_{\text{model}}dmodel = embedding dim
- HHH = 头数(num heads)
- 每头 Q/K 维度 = dkd_kdk,每头 V 维度 = dvd_vdv
- 通常 dk=dv=dmodel/Hd_k = d_v = d_{\text{model}} / Hdk=dv=dmodel/H
对应到 Mamba-2:
| 注意力参数 | Mamba-2 对应 | 含义 |
|---|---|---|
| dmodeld_{\text{model}}dmodel | ppp | token embedding 维度 |
| 头数 HHH | Mamba 块的并行分组数 | 不一定必须等于注意力的头数,但逻辑类似 |
| dkd_kdk | nnn | 状态维度(类似 Q/K 向量长度) |
| dvd_vdv | ppp | value 维度(等于输入输出维度) |
| Q/K 相似度 | Ct⊤BsC_t^\top B_sCt⊤Bs | n 维向量点积 |
| mask | LtsL_{ts}Lts | SSM 递推生成的时间掩码 |
3. 数学对应点
在 SSD 分解里:
Mts=Lts⋅(Ct⊤Bs)M_{ts} = L_{ts} \cdot (C_t^\top B_s) Mts=Lts⋅(Ct⊤Bs)
- Ct∈RnC_t \in \mathbb{R}^nCt∈Rn 类似 query
- Bs∈RnB_s \in \mathbb{R}^nBs∈Rn 类似 key
- Ct⊤Bs∈RC_t^\top B_s \in \mathbb{R}Ct⊤Bs∈R 类似注意力的相似度打分
- LtsL_{ts}Lts 是 SSM 的时间因果 mask(替代 softmax)
- xs∈Rpx_s \in \mathbb{R}^pxs∈Rp 类似 value
所以:
- nnn 决定 Q/K 向量长度(但它是状态空间维度,不一定等于 ppp)
- ppp 决定 value 维度(同时也是输入输出 token 的 embedding 维度)
4. 总结类比表
| 概念 | 注意力机制 | Mamba-2 |
|---|---|---|
| token embedding | dmodeld_{\text{model}}dmodel | ppp |
| Q/K 维度 | dkd_kdk | nnn |
| V 维度 | dvd_vdv | ppp |
| 相似度计算 | QK⊤QK^\topQK⊤ | Ct⊤BsC_t^\top B_sCt⊤Bs |
| mask | attention mask | LtsL_{ts}Lts(SSM 生成) |
| 归一化 | softmax | 无 softmax(直接乘) |
如果你愿意,我可以帮你画一个 Mamba-2 与 Attention 对照的结构图,把 nnn、ppp、Q/K/V、LtsL_{ts}Lts 的关系直观展示出来,这样更容易记。
你要我画这个图吗?
5. 注意头的数量和维度计算关系
Mamba-2中注意头的数量和维度关系怎么计算
我帮你把 Mamba-2 里“注意力头数”和维度关系的计算方法拆开讲一下,并且和多头注意力的公式对齐。
1. 基本变量
在 Mamba-2 一个 block 中,我们关心三个核心参数:
- ppp = 输入/输出 embedding 维度(相当于 Transformer 的 dmodeld_{\text{model}}dmodel)
- HHH = 头的数量(num heads,Mamba 里是分组并行的 SSM 数量)
- nheadn_{\text{head}}nhead = 每个头的状态维度(state dim per head,类似于注意力中每头的 dkd_kdk)
2. 维度分配公式
2.1 每头的输入维度
在多头注意力中,每头的输入维度是:
pper head=pHp_{\text{per head}} = \frac{p}{H} pper head=Hp
同理,在 Mamba-2 中也一样:
- 输入 xt∈Rpx_t \in \mathbb{R}^pxt∈Rp 被分成 HHH 份
- 每头的 token embedding 维度 = p/Hp / Hp/H
2.2 每头的状态维度
Mamba-2 的状态维度 nnn 是 per-head 定义的:
- 每个头的状态长度 = nheadn_{\text{head}}nhead
- 总状态长度 = ntotal=H×nheadn_{\text{total}} = H \times n_{\text{head}}ntotal=H×nhead
2.3 参数矩阵大小
Mamba-2 的核心两个矩阵:
- Bt∈Rnhead×pper headB_t \in \mathbb{R}^{n_{\text{head}} \times p_{\text{per head}}}Bt∈Rnhead×pper head
- Ct∈Rnhead×pper headC_t \in \mathbb{R}^{n_{\text{head}} \times p_{\text{per head}}}Ct∈Rnhead×pper head
总参数量:
Params≈2×H×(nhead×pH)=2×p×nhead\text{Params} \approx 2 \times H \times \left( n_{\text{head}} \times \frac{p}{H} \right) = 2 \times p \times n_{\text{head}} Params≈2×H×(nhead×Hp)=2×p×nhead
可以看到:
- 头数 HHH 对总参数量没直接影响(分头后乘除抵消)
- 总参数量取决于 ppp 和 nheadn_{\text{head}}nhead
3. 和多头注意力的类比
| 多头注意力参数 | Mamba-2 对应 | 说明 |
|---|---|---|
| dmodeld_{\text{model}}dmodel | ppp | token embedding dim |
| 头数 HHH | 头数 HHH | 分组数量 |
| 每头 dkd_kdk | nheadn_{\text{head}}nhead | 状态维度 per head |
| 每头 dvd_vdv | pper headp_{\text{per head}}pper head | 输入/输出通道数 per head |
4. 计算示例
假设:
- p=1024p = 1024p=1024
- H=8H = 8H=8
- nhead=64n_{\text{head}} = 64nhead=64
那么:
- 每头输入维度:
pper head=10248=128p_{\text{per head}} = \frac{1024}{8} = 128 pper head=81024=128
- 总状态维度:
ntotal=8×64=512n_{\text{total}} = 8 \times 64 = 512 ntotal=8×64=512
- 参数量:
Params≈2×1024×64=131,072\text{Params} \approx 2 \times 1024 \times 64 = 131{,}072 Params≈2×1024×64=131,072
5. 设计经验
-
HHH 越大 → 每头输入维度变小(更细分并行,适合大模型)
-
nheadn_{\text{head}}nhead 越大 → 每头记忆容量越大(长依赖更强)
-
通常 nheadn_{\text{head}}nhead 不超过 pper headp_{\text{per head}}pper head,否则状态会比输入维度还宽,计算量上升很多
-
常用配置:
- 小模型:H=4,nhead=64H=4, n_{\text{head}}=64H=4,nhead=64
- 中模型:H=8,nhead=128H=8, n_{\text{head}}=128H=8,nhead=128
- 大模型:H=16,nhead=256H=16, n_{\text{head}}=256H=16,nhead=256
如果你需要,我可以帮你画一个 Mamba-2 多头维度关系图,把 ppp、HHH、nheadn_{\text{head}}nhead 直观画出来,这样一眼就能看出公式和分配关系。
你要我画这个图吗?
