NLP学习路线图（三）： 微积分（梯度、导数等）

引言

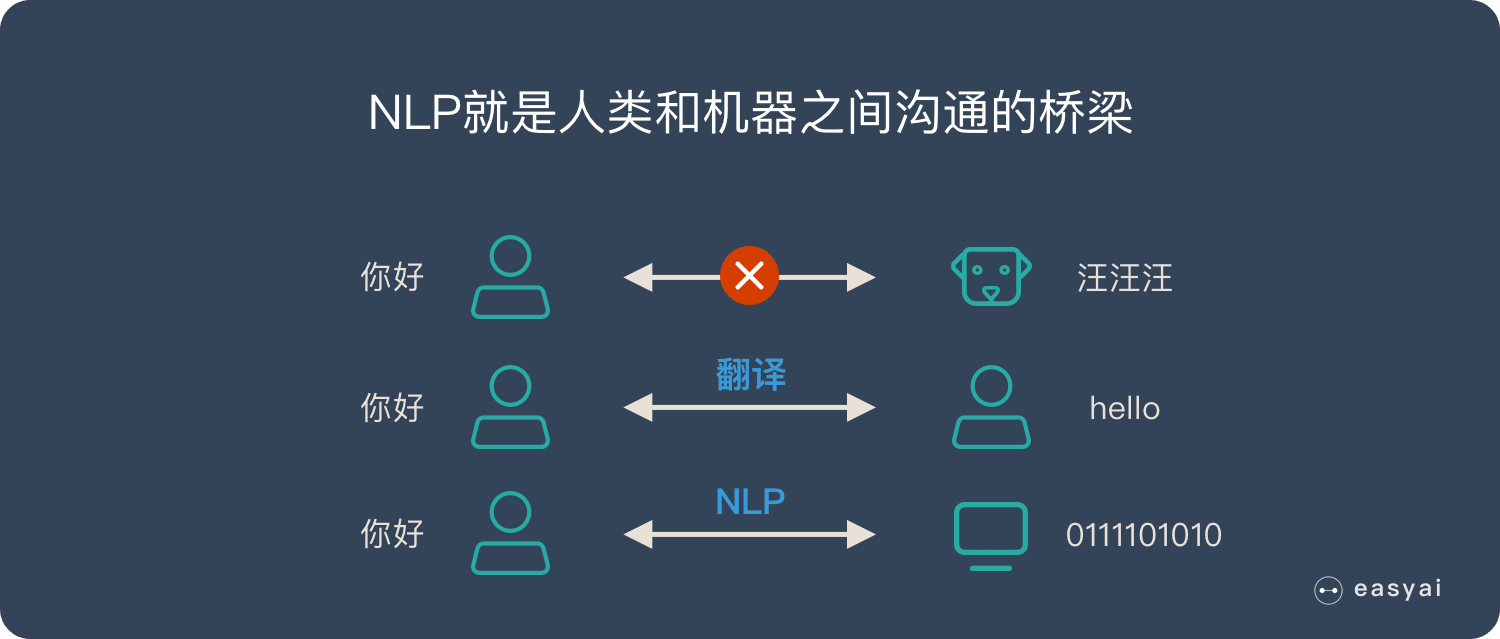
自然语言处理（NLP）是人工智能领域的重要分支，涉及语言理解、文本生成、机器翻译等任务。尽管现代NLP模型（如BERT、GPT）依赖深度学习技术，但其底层数学原理始终是核心支撑。微积分作为数学的基石之一，在模型优化、特征学习和算法设计中扮演着关键角色。本文将深入探讨导数、梯度等概念在NLP中的应用，并通过实例解析它们如何驱动模型训练与改进。

第一部分：导数与微分基础

1.1 导数的定义与几何意义

导数是微积分的核心概念，描述函数在某一点处的变化率。对于函数 f(x)，其在点 x0​ 处的导数定义为：

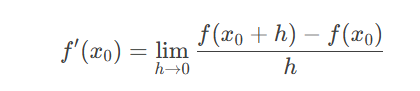
几何上，导数对应函数曲线在该点的切线斜率。例如，在NLP中，若某损失函数 L(θ) 随参数 θ 的变化而变化，导数 L′(θ) 可以指导参数调整的方向。

1.2 常见函数的导数规则

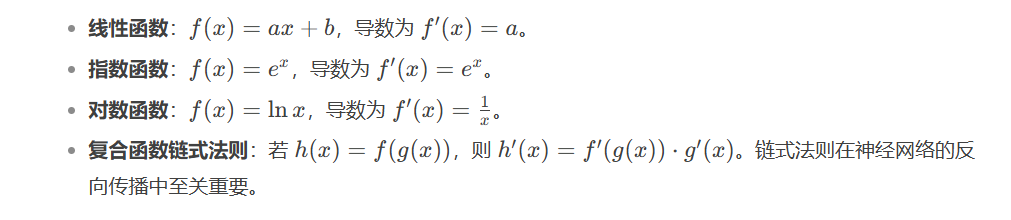
1.3 偏导数与多变量函数

第二部分：梯度与方向导数

2.1 梯度的定义与几何解释

梯度是多变量函数的导数推广。对于函数 f(x1,x2,…,xn)f(x1​,x2​,…,xn​)，其梯度是一个向量：

 

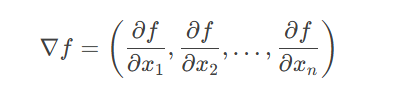
几何意义：梯度指向函数在该点处上升最快的方向，模长表示变化率。在优化问题中，负梯度方向即为函数下降最快的方向。

2.2 梯度下降算法

梯度下降是NLP模型训练的核心算法，通过迭代更新参数以最小化损失函数：

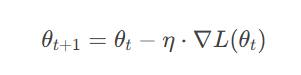
其中 η 为学习率。
实例：在训练语言模型时，损失函数 LL 衡量预测词与真实词的差异，梯度 ∇L 指示如何调整词向量矩阵和神经网络权重。

2.3 随机梯度下降（SGD）与小批量优化

由于NLP数据规模庞大，直接计算全量数据的梯度计算成本高。SGD通过随机采样小批量数据近似梯度：

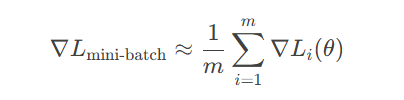
 此方法显著提升了训练效率，并成为深度学习框架（如PyTorch、TensorFlow）的默认优化策略。

第三部分：微积分在NLP中的核心应用

3.1 损失函数的优化

NLP任务通常转化为优化问题。例如：

• 交叉熵损失：用于分类任务（如文本分类），其梯度计算涉及Softmax函数的导数。

• 均方误差（MSE）：用于回归任务（如词向量平滑），梯度计算更简单。

3.2 反向传播与链式法则

反向传播是神经网络训练的基石，其本质是微积分中链式法则的高效实现。以简单的全连接网络为例：

第四部分：高级话题与挑战

4.1 优化算法的改进

• 动量法（Momentum）：引入历史梯度方向，加速收敛。

• Adam：结合动量与自适应学习率，适用于稀疏数据（如文本）。

4.2 梯度消失与爆炸问题

在深度网络（如RNN）中，梯度可能因连续乘法变得极小（消失）或极大（爆炸）：

• 解决方案：

  • 梯度裁剪（Gradient Clipping）：限制梯度最大值。

  • LSTM/GRU结构：通过门控机制缓解长程依赖问题。

4.3 二阶导数与海森矩阵

海森矩阵 H(f)H(f) 包含函数的二阶偏导数，可用于牛顿法优化：

 

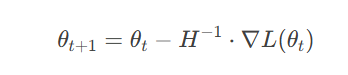
尽管计算成本高，但在部分优化场景（如参数较少时）仍有应用。 

结语

微积分为NLP提供了优化模型的理论基础，从简单的逻辑回归到复杂的Transformer都依赖梯度计算。理解导数、梯度与链式法则，不仅能帮助开发者调试模型，还能为改进算法提供方向。未来，随着自动微分（Autograd）技术的成熟，微积分的应用将更加隐式但不可或缺。