每天五分钟深度学习：神经网络的梯度下降和反向传播算法

本文重点

在深度学习领域，神经网络通过模拟人脑神经元连接机制实现复杂模式识别与决策。其训练过程依赖两个核心算法：梯度下降用于优化模型参数，反向传播用于高效计算参数梯度。二者协同工作，构成神经网络从数据中学习的数学基础。

数学引擎

算法本质与数学原理

梯度下降通过迭代调整参数，使损失函数（如交叉熵、均方误差）逐步减小。其核心思想源于微积分中的方向导数理论：函数在某点的梯度方向是增长最快的方向，负梯度方向则是下降最快的方向。数学表达式为：

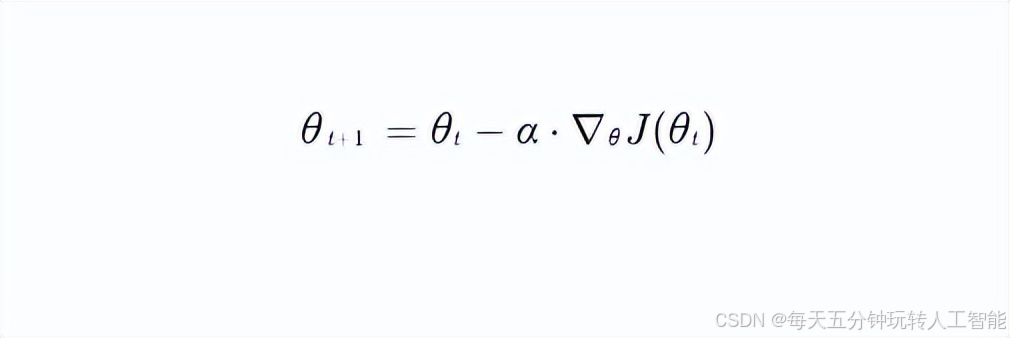
其中：

• θ为模型参数（如权重和偏置）
• α为学习率（控制步长）
• J(θ)为损失函数
• ∇θ​表示对参数的梯度计算

链式法则

链式法则将复合函数的导数分解为多个简单函数的导数乘积。例如，对于损失函数

</
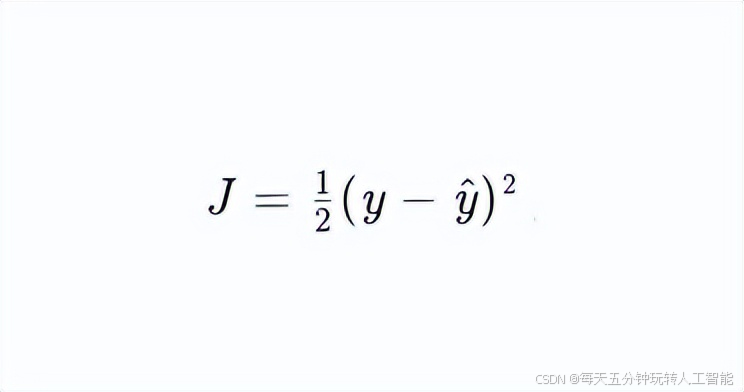