hot100——第十周
目录
买卖股票的最佳时机
跳跃游戏
跳跃游戏 II
灌溉花园的最少水龙头数目
划分字母区间
数组中的第K个最大元素
前 K 个高频元素
数据流的中位数
打家劫舍
打家劫舍 II
买卖股票的最佳时机
解法:贪心
遍历到当前天数时找到前面最小的值进行相减得到当前最大利润,遍历最大值
class Solution
{
public:int maxProfit(vector<int> &prices){int ret = 0, min_price = prices[0];for (int i = 1; i < prices.size(); i++){min_price = min(min_price, prices[i]);ret = max(ret, prices[i] - min_price);}return ret;}
};跳跃游戏
解法:枚举
使用一个最大距离值 max_distance 表示当前能够跳跃到的最大距离;
遍历数组一遍枚举更新 max_distance,当 max_distance < i 说明走不到i位置,返回false;
遍历结束说明可以走到 n-1 位置,返回true
class Solution
{
public:bool canJump(vector<int> &nums){int max_distance = 0, n = nums.size();for (int i = 0; i < n; i++){if (max_distance < i)return false;max_distance = max(max_distance, nums[i] + i);}return true;}
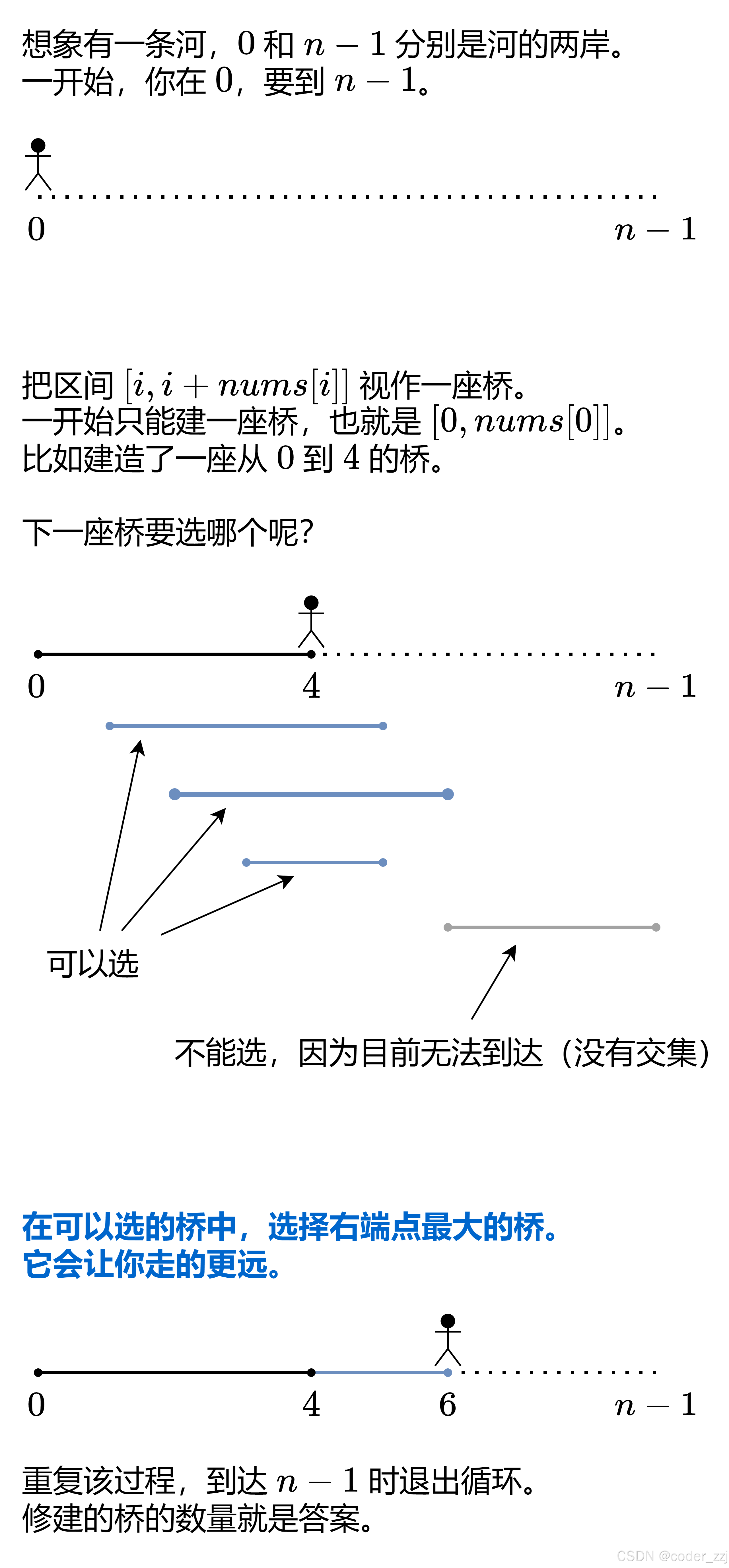
};跳跃游戏 II
解法:贪心
把遍历的过程比作修桥:
当走到当前修桥最右边无路可走时就要修最远到达的桥(前面遍历中的最大值)
class Solution
{
public:int jump(vector<int> &nums){int ret = 0, n = nums.size();int cur_right = 0, max_right = 0;for (int i = 0; i < n - 1; i++){max_right = max(max_right, nums[i] + i);// 走到当前最右边后开始修最远到达的桥if (cur_right == i){ret++;cur_right = max_right;}}return ret;}
};思路2:区间问题
定义左右区间:每次通过区间内的最大值,更新下一次的右区间(左区间就是原来的右区间+1)(更新一次相当于修了一次最远的桥)
当更新的右区间大于等于最后一个值就可以返回
class Solution
{
public:int jump(vector<int> &nums){int ret=0,n=nums.size();int l=0,r=0;while(true){if(r>=n-1) return ret;ret++;int max_dis=0;for(int i=l;i<=r;i++) max_dis=max(max_dis,nums[i]+i);l=r+1,r=max_dis;}return -1;}
};灌溉花园的最少水龙头数目
与上题思路类似,但要进行预处理一个数组表示:当前位置i到达右边的最远位置
还要特殊判断到不了n位置时就要返回-1
class Solution
{
public:int minTaps(int n, vector<int> &ranges){int m = ranges.size();vector<int> max_right_arr(m);for (int i = 0; i < m; i++){// 当前位置能够到达左边最远位置int max_left = max(i - ranges[i], 0);// 通过max_left位置更新出右边最远的位置(可以把最大值控制到n,也可以不控制)max_right_arr[max_left] = min(max(max_right_arr[max_left], i + ranges[i]), n);}for (auto &m : max_right_arr)cout << m << ' ';// 跳跃游戏Ⅱ 思路:修桥int cur_right = 0, max_right = 0, ret = 0;for (int i = 0; i < m - 1; i++) // 遍历到倒数第二个位置{max_right = max(max_right, max_right_arr[i]);if (i == cur_right){if (i == max_right)return -1; // 当前位置到不了nret++;cur_right = max_right;}}return ret;}
};划分字母区间
思路:此题本质还是跳跃游戏Ⅱ的思路,只不过还是要与上题一样:先预处理出一个每个字符最远达到位置,然后就来进行“修桥”
class Solution
{
public:vector<int> partitionLabels(string s){int arr[26] = {0}, n = s.size();// 存字符最远达到的位置for (int i = 0; i < n; i++){arr[s[i] - 'a'] = max(arr[s[i] - 'a'], i);}int begin = 0, end = 0;vector<int> ret;for (int i = 0; i < n; i++){int max_pos = arr[s[i] - 'a'];// 遍历最远位置end = max(end, max_pos);// 当前最远位置到了if (end == i){ret.push_back(end - begin + 1);// 更新下一个片段end = i + 1;begin = end;}}return ret;}
};数组中的第K个最大元素
解法1:最大堆
元素扔到最大堆中,取第k个最大元素
解法2:分治
使用快排的数组分三块思想,在递归前判断是否可以返回第k个最大元素
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {priority_queue<int> q;for (auto& num : nums) q.push(num);while (--k) q.pop();return q.top();}
};class Solution {
public:int quick_sort(vector<int>& nums, int k, int begin, int end){if (begin >= end) return nums[begin];int l = begin - 1, r = end + 1;int key = nums[rand() % (end - begin + 1) + begin];//[begin,l]-> key [l+1,i]-> =key [i+1,r-1]->带扫描 [r,end]-> >keyfor (int i = begin; i < r;){if (nums[i] < key) swap(nums[++l], nums[i++]);else if (nums[i] > key) swap(nums[--r], nums[i]);else i++;}//[begin,l] [l+1,r-1] [r,end]if (end - r + 1 >= k) return quick_sort(nums, k, r, end);//到这里:end-i+1<k 一定不在[i,end]区间 if (end - (l + 1) + 1 >= k) return nums[l + 1];return quick_sort(nums, k - (end - (l + 1) + 1), begin, l);}int findKthLargest(vector<int>& nums, int k) {srand(time(nullptr));return quick_sort(nums, k, 0, nums.size() - 1);}
};前 K 个高频元素
解法:最大堆
使用哈希进行统计元素个数后将数据扔到最大堆中,取k个最大堆的元素
class Solution {
public:vector<int> topKFrequent(vector<int>& nums, int k) {auto fun = [](pair<int, int>& p1, pair<int, int>& p2){return p1.second < p2.second;};priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(fun)> q;map<int, int> hash;for (auto& num : nums) hash[num]++;for (auto& [a, b] : hash) q.push({ a,b });vector<int> ret;while (k--){auto& [a, b] = q.top();ret.push_back(a);q.pop();}return ret;}
};数据流的中位数
解法:大小堆
找中位数:本质在排完数的元素中分成左右两部分
- (偶数)左右个数相同,中位数就是左部分的最大与右部分的最小的平均数
- (奇数)(严格规定)左比右多一个,中位数就是左部分的最大值
左右个数一定满足:左个数 >= 右个数
那么:如果左边与右边个数相同,就把元素放到右边,右边里面元素的最小值给左边
否则(一定是左边个数比右边多1,就把元素放到左边,左边里面元素的最大值给右边)
class MedianFinder {
private:priority_queue<double> left;priority_queue<double, vector<double>, greater<double>> right;
public:MedianFinder() {}void addNum(int num) {//个数相同时:直接把num给right.right的最小值给leftif (left.size() == right.size()){right.push(num);double tmp = right.top(); right.pop();left.push(tmp);}//否则就放过来(此时一定是left个数比right多一个)else{left.push(num);double tmp = left.top(); left.pop();right.push(tmp);}}double findMedian() {if (left.size() == right.size()) return (left.top() + right.top()) / 2;return left.top();}};打家劫舍
动态规划的多状态问题
class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();vector<int> steal(n + 1), nosteal(n + 1);for (int i = 1; i <= n; i++){steal[i] = max(steal[i - 1], nosteal[i - 1] + nums[i - 1]);nosteal[i] = max(nosteal[i - 1], steal[i - 1]);}return max(steal[n], nosteal[n]);}
};解法2:递归
dfs[i]:第i位置的最高金额,以偷不偷作为切入点
如果偷,那么问题就转化成 前i-2个位置的最高金额 dfs[i-2] + nums[i]
如果不偷,那么问题就转化成 前i-1个位置的最高金额 dfs[i-1]
取二者的最大值
这样递归从重复数据,可以使用数组进行记忆化
class Solution:def rob(self, nums: List[int]) -> int:n = len(nums)cache = [-1] * ndef dfs(i) -> int:if i < 0:return 0if cache[i] != -1:return cache[i]ret = max(dfs(i-1),dfs(i-2) + nums[i])cache[i] = retreturn retreturn dfs(n-1)1比1翻译成递归(动态规划),需要添加2个空格保证不越界
还可以继续优化成 O(1)空间:dfs(i-1)是dfs(i)的前一个状态,dfs(i-2)是dfs(i)的前前一个状态
class Solution:def rob(self, nums: List[int]) -> int:n = len(nums)# dp = [0] * (n+2)f1 = 0f2 = 0for i in range(2,n+2):# dp[i] = max(dp[i-1],dp[i-2] + nums[i-2])new_f = max(f1,f2 + nums[i-2])f2 = f1f1 = new_freturn f1打家劫舍 II
规划区间进行打家劫舍:【0,n-2】或者【1,n-1】范围内进行打家劫舍,取最大值
class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();if (n == 1) return nums[0];return max(dp(nums, 0, n - 2), dp(nums, 1, n - 1));}int dp(vector<int>& nums, int begin, int end){int n = nums.size();vector<int> steal(n), nosteal(n);steal[begin] = nums[begin];for (int i = begin + 1; i <= end; i++){steal[i] = max(steal[i - 1], nosteal[i - 1] + nums[i]);nosteal[i] = max(nosteal[i - 1], steal[i - 1]);}return max(steal[end], nosteal[end]);}
};以上便是全部内容,有问题欢迎在评论区指正,感谢观看!
