贝叶斯定理

【2025中英双版】吴恩达机器学习数学基础【概率论与统计】Probability Theory and Statistics--机器学习/数学基础_哔哩哔哩_bilibili

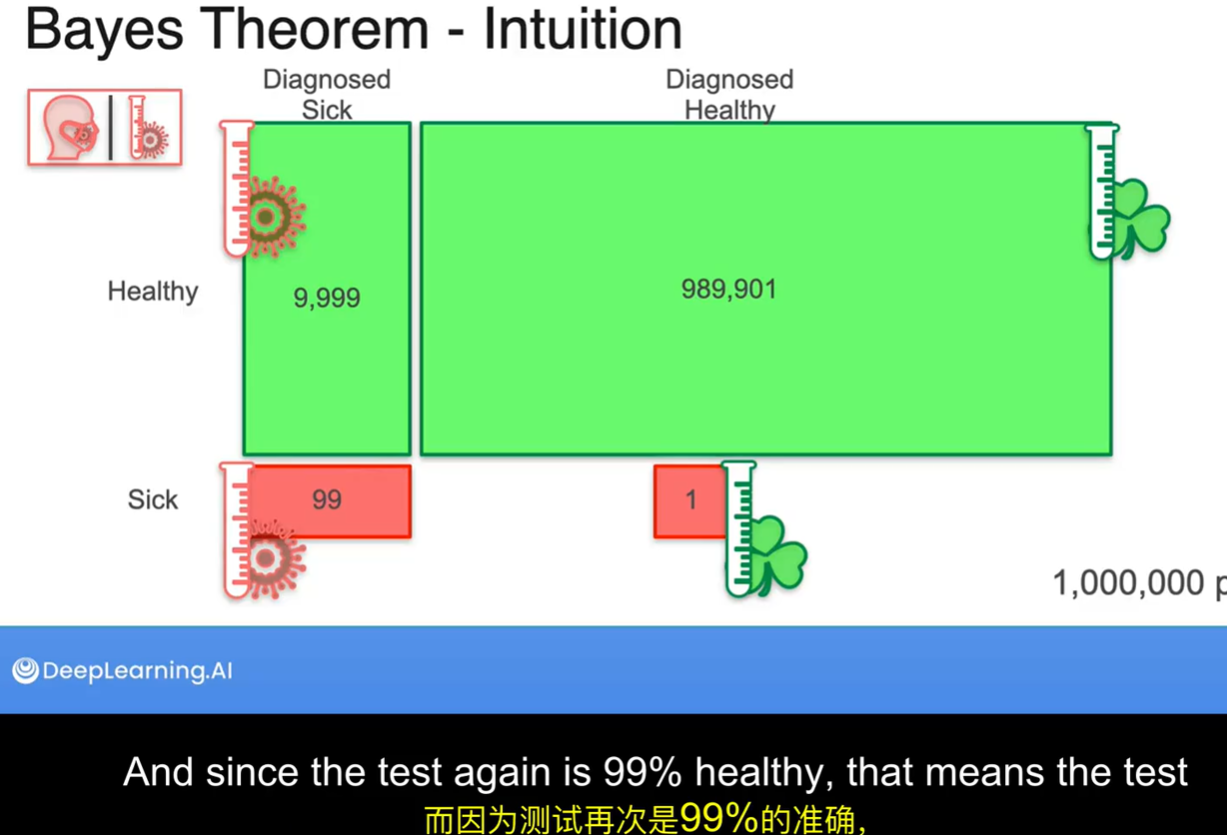
健康的人有百分之1被误诊 

有病的人也有百分之1被误诊

看你是健康的人被误诊还是有病的人被正确诊断

健康的人被误诊的数目远远大于有病的人被正确诊断的数目

有病的人数太少，而误诊人数又太多，你还是不容易成为有病的人

降低准确度只会拉大误诊的人数的差距

只有这个病发生的概率提高才会减少误诊的人数

如果发病概率百分之1的情况

100万人

99万没病 0.99万人被误诊 

人数（没病误诊）=（1-p（得病率））*100万*p（误诊）

=（p（误诊）-p（误诊）*p（得病率））*100万

1万人有病 9.9千人是正确诊断

人数（有病正确诊断）=p（得病率）*100万*（1-p（误诊））

=（p（得病率）-p（得病率）*p（误诊））*100万

概率就变成一半一半

p（误诊）=p（得病率）的时候两边相等

p真的有病=人数（有病正确诊断）/（人数（没病误诊）+人数（有病正确诊断））

如果得病的概率高于误诊率，就容易真的有病

突然看不懂

p（A|B）=p（认为有病 并且也 得病了）

=p（的病了 认为有病）/p（认为有病）

p（A）*P（B|A）=p（得病的情况）*p（得病的情况  认为有病）

p（A‘）*p（B|A’）=p（没得病的情况）*p（没得病的情况  认为有病）

p（ B）=p（认为有病）=p（A）*P（B|A）+p（A‘）*p（B|A’）

p（ B）=p（（A∪A’）∩B）=p（A∩B）+p（A‘∩B）

P（A∩ B）=P(A|B)*P(B)=P(B|A)*P(A)

p（A‘∩B）=p（A’|B）*P（B）=p（B|A‘）*P（A’）  求p（B）了就不可能用P（B）了

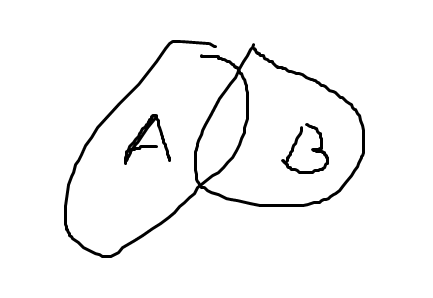
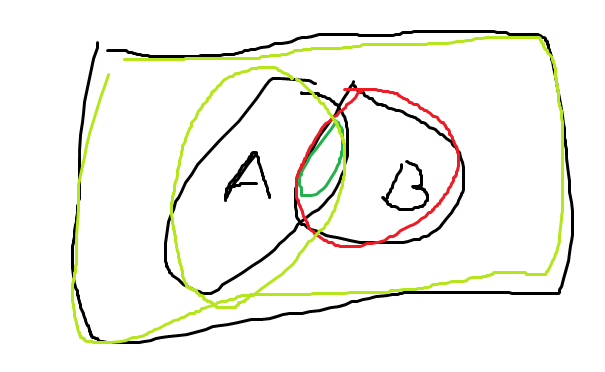
再回来看这个公式

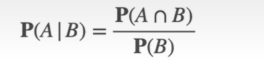
求p(A|B)=P(A∩B)/P（B）因为求的前提是B发生所以B在底  P（A|B）*P（A）也乘不出什么东西

或者直接看图

 可见p(A|B)=p（与A有关的部分在B里的概率）=P(A∩B)/P（B）

求这个P（A|B）

起码要知道P（A）和P（B|A）

P（B|A‘）=P（B∩A’）/P（A‘）

P（B∩A’）=P（A‘|B）*P（B）

P（B|A‘）+P（B|A）=莫得