当前位置：首页 > java >正文

三维重建线结构光之重建原理（单线结构光为例）

java 2025/9/4 19:35:20

通过上一篇文章，可以求得激光在空间中的光平面方程。如果以单目相机+单激光投影来进行举例。假设系统标定已完成。
当进行重建时已知：

条纹中心点 $P (x, y)$ (在归一化平面下).
光平面方程
求：
在相机坐标系下的三维空间点坐标 $P_c(X_c,Y_c,Z_c)$

单线结构光重建原理

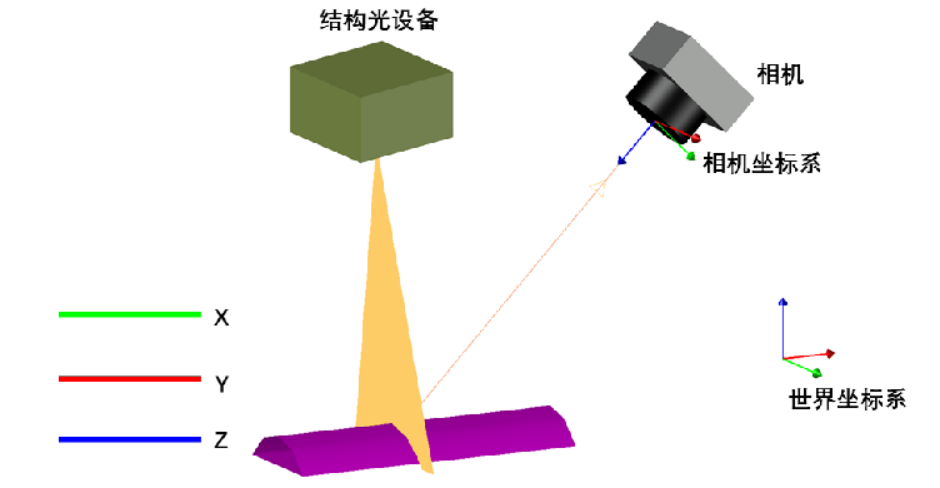
单线结构光测量系统模型包含一个用于采集图像的相机和一个单线结构光发射器，系统构成较为简单。测量过程中，结构光映射到物体表面，相机获取物体表面调制的具有一定分布的激光条纹，并提取激光条纹的中心点像素坐标，利用激光三角测量法计算得到中心点对应的三维空间坐标。（为了获取光线所对应的光平面方程）
在这里插入图片描述
激光条纹中心点 $P_I(u,v)$ 对应的在相机坐标系（CCS）下的三维空间坐标 $P_c(X_c,Y_c,Z_c)$ 和归一化平面中的二维坐标 $P (x, y)$ （归一化平面（normalized image plane）是一个虚拟的平面，通常位于相机坐标系 $Z_c =1$ 的位置。）, 则在每个坐标轴上投影的坐标如图
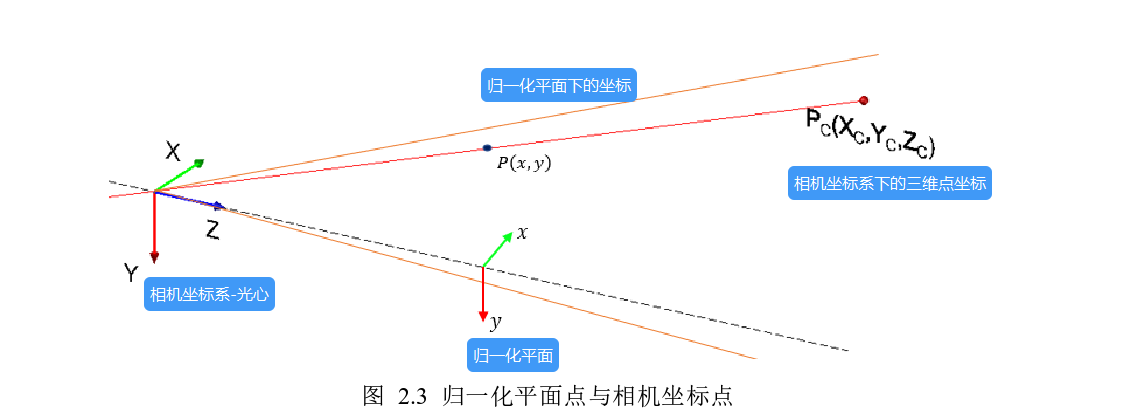
在这里插入图片描述
两个点在坐标轴上的投影分量满足如下比例关系
$\frac{x}{X_c} = \frac{y}{Y_c} = \frac{1}{Z_c} \tag{2-4}$
由于激光条纹中心点在空间中属于激光平面，因此空间点 $P_C$ 还满足其所在的光平面方程，（通过标定可得a b c 与 d）
$\; aX_c + bY_c + cZ_c = d \tag{2-5}$

计算步骤如下：由方程2-4可知
$\frac{X_c}{Z_c}, \quad y = \frac{Y_c}{Z_c}\tag{2-6}$
将2-6带入2-5，可得
$a(xZ_c) + b(yZ_c) + cZ_c = d\tag{2-7}$
$Z_c (ax + by + c) = d\tag{2-8}$
因此，可得
$Z_c = \frac{d}{ax + by + c}\tag{2-9}$
$X_c = \frac{dx}{ax+by+c}, \quad Y_c = \frac{dy}{ax+by+c} \tag{2-10}$
通过以上关系式可得知归一化平面中的条纹中心点与相机坐标系下的三维空间点的映射关系.

相机坐标系下的三维点与归一化平面中的坐标映射关系为：
$\begin{pmatrix} X_c \\ Y_c \\ Z_c \end{pmatrix} = \frac{d}{ax + by + c} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \tag{2-11}$
通过相机模型，我们知道像素坐标系与归一化平面坐标系之间的关系为摄像机的内参矩阵K。
$\begin{pmatrix} u \\ v \\ 1 \end{pmatrix} =K \begin{pmatrix} x_n \\ y_n \\ 1 \end{pmatrix} =\begin{pmatrix}f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{pmatrix}\begin{pmatrix} x_n \\ y_n \\ 1 \end{pmatrix}\tag{2-12}$