当前位置：首页 > java >正文

深度学习中常用的激活函数

java 2025/9/2 6:24:19

参考文章：

Activation Functions — All You Need To Know! | by Sukanya Bag | Analytics Vidhya | Medium

深度学习笔记：如何理解激活函数？（附常用激活函数） - 知乎

part-0_13.pdf

机器学习中的数学——激活函数（十一）：Softsign函数_softsign激活函数-CSDN博客

激活函数（Activation Function）

在深度学习中，对于一个神经网络，我们通常会在每一层神经网络的输出后面使用一个函数对结果进行运算，这个函数就是激活函数（Activation Function）。

如果没有激活函数会怎样？

那么每一层的输出都只是上一层输入的线性组合。无论你的网络有多深，整个模型最终都等价于一个单层线性模型。这极大地限制了网络的能力，使其无法学习复杂、非线性的 patterns。

激活函数的作用：

引入非线性（Non-linearity）：这是最主要的作用。通过非线性的激活函数，神经网络可以逼近任意复杂的非线性函数。
决定神经元是否激活：类似于生物神经元中的“全或无”定律，激活函数可以根据输入信号的强度，决定该神经元是保持静息（输出0或一个很小的值）还是被激发（输出一个较大的值）。

1、常用的激活函数

1.1 Sigmoid函数

Sigmoid 函数也叫 Logistic 函数，取值范围为 (0,1)，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。

公式：

$\mathrm{sigmoid}(x) = \frac{1}{1 + e^{-x}}$

值域： (0, 1)

图像：

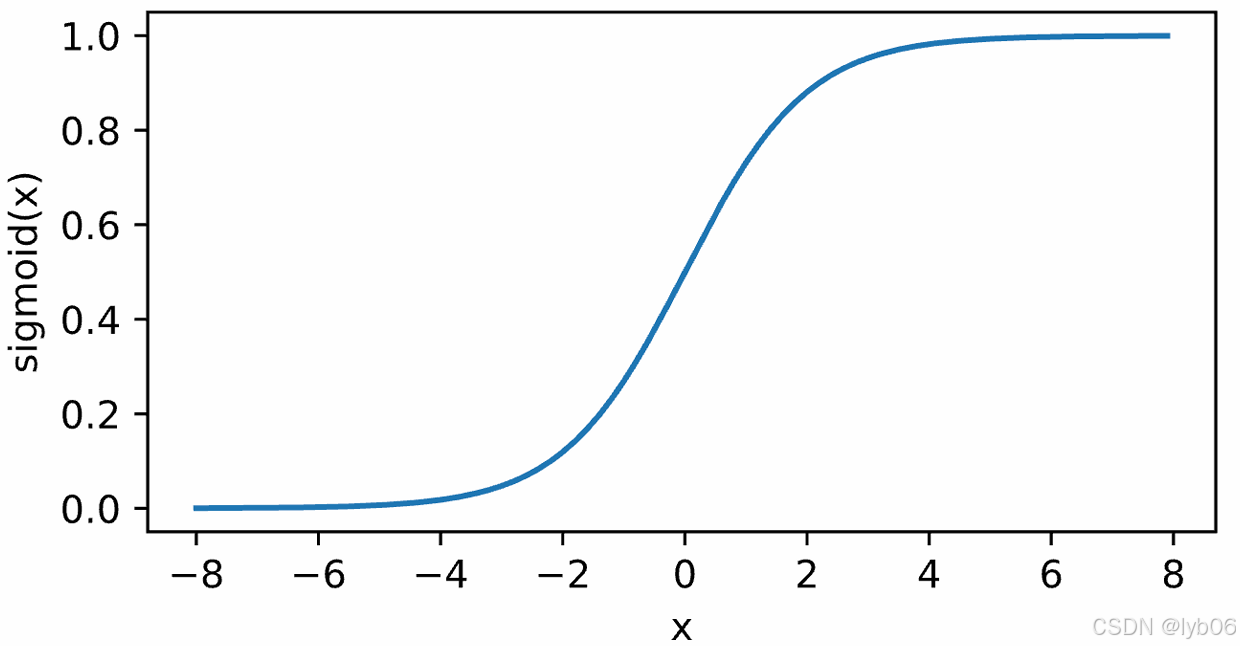
优点：

将输出平滑地压缩到0和1之间，非常适合作为二分类模型输出层的激活函数（可以理解为概率）。

缺点：

梯度消失（Vanishing Gradient）：当输入 x 的绝对值很大时，函数的梯度（导数）会变得非常小，接近于0。在反向传播过程中，梯度会层层连乘，导致靠前的网络层权重更新非常缓慢，甚至无法学习。
输出非零中心（not zero-centered）：其输出恒大于 0。这会导致后续神经元的输入全部为正，在梯度下降时，权重的更新方向会被“捆绑”，优化路径呈锯齿状，收敛速度变慢。
计算成本高昂：计算涉及指数，相对较慢。

使用场景：

用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1，因此 Sigmoid 函数非常合适。

1.2 Tanh函数

Tanh 函数也叫双曲正切函数函数。Tanh 函数与 Sigmoid 函数很相似，但是 Tanh 函数的输出取值范围为 [-1, 1]，并且 Tanh 函数的输出以零为中心。

公式：

$\mathrm{tanh}(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} =\frac{1 - e^{-2x}}{1 + e^{-2x}} =\frac{2}{1 + e^{-2x}}-1$

值域： (-1, 1)

图像：

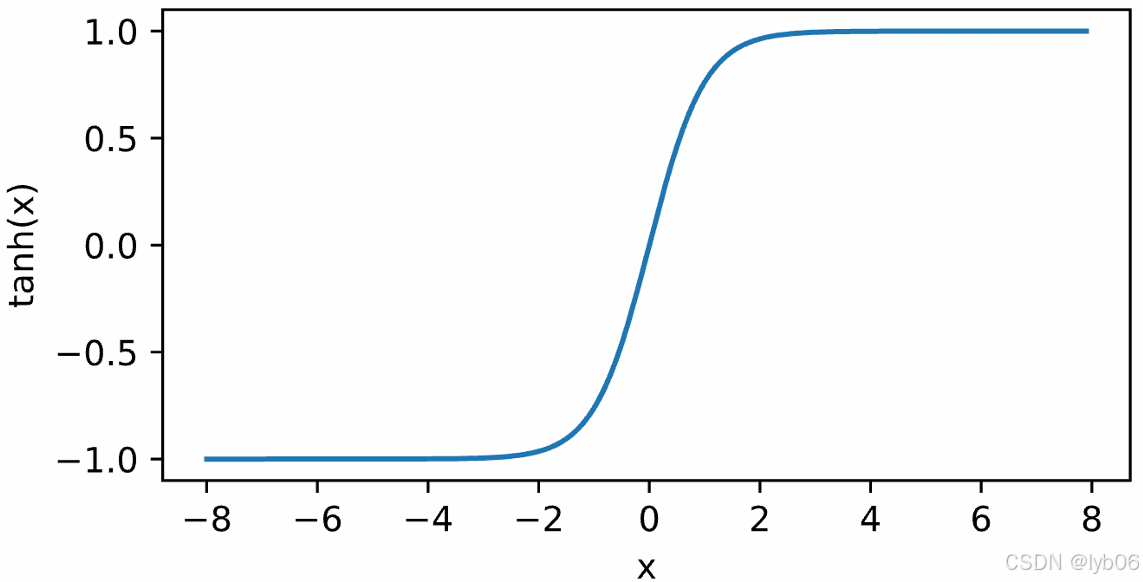
可以发现 Tanh 函数可以看作放大并平移的 Sigmoid 函数，它们之间的关系如下：

$\mathrm{tanh}(x)=2\mathrm{sigmoid}(2x)-1$

二者图像的对比：

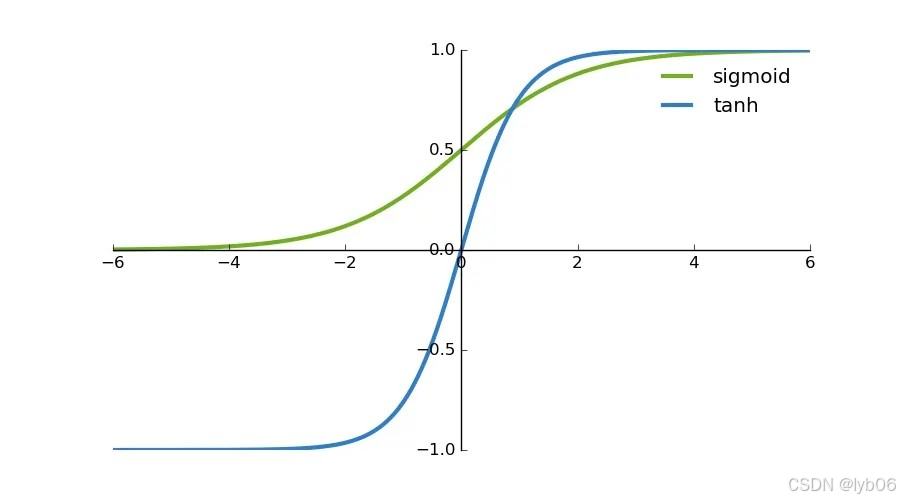
优点：

tanh 是 Sigmoid 的缩放版。它解决了 Sigmoid 输出非零中心的问题，因其输出以 0 为中心，收敛速度通常比 Sigmoid 快。

缺点：

仍然存在梯度消失问题

1.3 ReLU函数

ReLU 函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了 sigmoid 函数以及 tanh 函数的梯度消失问题，在目前的深度神经网络中被广泛使用。

公式：

$\begin{aligned} \mathrm{ReLU}(x) &=\begin{cases} x,\quad x>=0\\ 0,\quad x<0 \end{cases}\\ &= \max(0, x) \end{aligned}$

值域： [0, +∞)

图像：

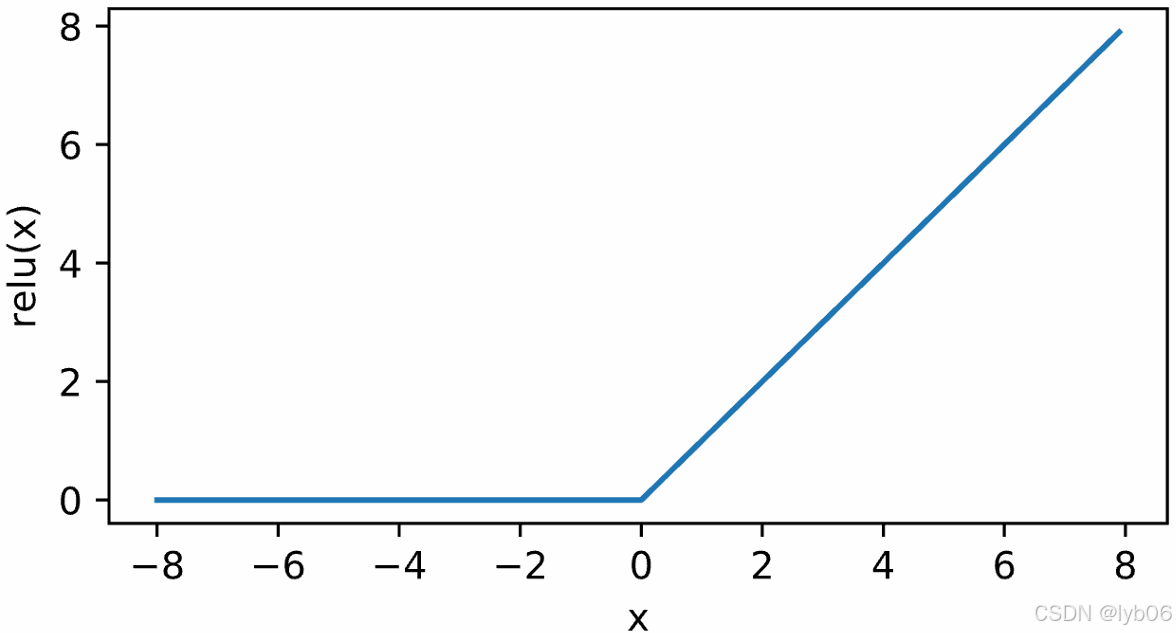
优点：

计算极其高效：就是简单的阈值判断，没有指数等复杂运算。
在正区间（x > 0）解决了梯度消失问题，梯度恒为1，使得反向传播非常高效。
收敛速度远快于 Sigmoid 和 Tanh。

缺点：

Dying ReLU（神经元死亡）问题：当输入为负时，输出和梯度都为0。一旦一个神经元落入这种情况，在后续训练中它的权重可能再也不会更新，该神经元就永久“死亡”了。

输出不以零为中心：和 Sigmoid 激活函数类似，ReLU 函数的输出不以零为中心，ReLU 函数的输出为 0 或正数，给后一层的神经网络引入偏置偏移，会影响梯度下降的效率。

尽管有缺点，ReLU 及其变体仍然是目前隐藏层中最主流、最常用的激活函数。

1.4 Leaky ReLU函数

为了解决 ReLU 激活函数中的梯度消失问题，当 x < 0 时，我们使用 Leaky ReLU（带泄露的ReLU）函数试图修复 dead ReLU 问题。

公式：

$\begin{aligned} \mathrm{LeakyReLU}(x) &= \begin{cases} x,\quad \mathrm{if}\quad x>0\\ \alpha x,\quad \mathrm{if}\quad x\le0 \end{cases}\\ &=\max(\alpha x, x)\\ &=\max(0,x)+\alpha \min(0,x) \end{aligned}$

其中 α 是一个很小的数，如 0.1，0.01等等。

值域：(-∞, +∞)

图像：以 α=0.1 为例

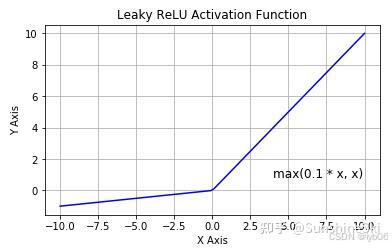
ReLU 和 Leaky ReLU 的图像对比：

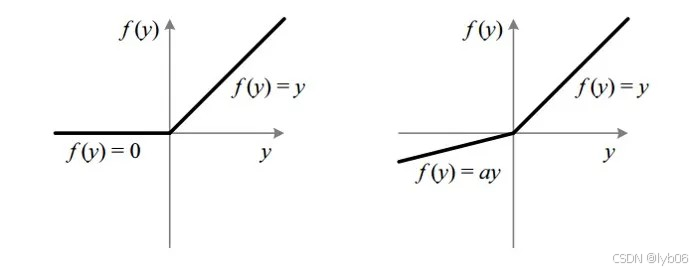
优点：

针对 ReLU 的“死亡”问题进行了改进。当 x < 0 时，它有一个很小的斜率 α，而不是直接为 0。这确保了负区间也有梯度，避免了神经元死亡的问题。

缺点：

效果并不总是稳定，且需要手动设置 α 参数（虽然通常设为 0.01）。

1.5 Parametric ReLU函数

Parametric ReLU（带参数的ReLU）是 Leaky ReLU 的进阶版。Leaky ReLU 在负区间引入了斜率 α，这个 α 是一个预先设定好的值。而 Parametric ReLU 将这个负区间的斜率 α 也作为一个可学习的参数，让网络自己决定负区间的斜率应该是多少，更加灵活。

公式：

$\begin{aligned} \mathrm{PReLU}(x) &= \begin{cases} x,\quad \mathrm{if}\quad x>0\\ \alpha_i x,\quad \mathrm{if}\quad x\le0 \end{cases}\\ &=\max(\alpha_i x, x)\\ &=\max(0,x)+\alpha_i \min(0,x) \end{aligned}$

其中 $\alpha_i$ 是一个超参数，可以通过反向传播进行学习。不同神经元可以有不同的参数，其中的 i 对应了第 i 个神经元，这使神经元能够选择负区域最好的梯度。

PReLU 函数中，参数 α 通常为 0 到 1 之间的数字，并且通常相对较小。

如果 $\alpha_i=0$ ，那么 PReLU 就退化为 ReLU。
如果 $\alpha_i$ 是一个很小的正常数，那么 PReLU 可以看作 Leaky ReLU。

优点：

PReLU 可以允许不同神经元具有不同的参数，也可以一组神经元共享一个参数。

在多数情况下，最好使用 ReLU，但是你可以使用 Leaky ReLU 或 Parametric ReLU 进行实践，看看哪一种方式更适合你的问题。

1.6 ELU函数

ELU（Exponential Linear Unit）的提出同样也是针对解决 ReLU 负数部分存在的问题，由 Djork 等人提出，被证实有较高的噪声鲁棒性。ELU 负区间是一个指数函数，正区间与 ReLU 相同。与 ReLU 相比，ELU 有负值，这会使激活的平均值接近零。激活均值接近于零可以使学习更快，因为它们使梯度更接近自然梯度。

公式：

$\mathrm{ELU}(x) = \begin{cases} x,\quad \mathrm{if}\quad x>0\\ \alpha (e^x-1),\quad \mathrm{if}\quad x\le0 \end{cases}\\$

值域： (-∞, +∞)

图像：

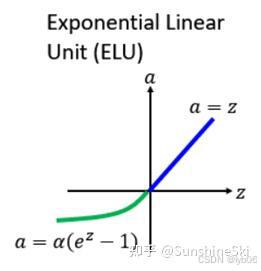
ELU、Leaky ReLU 和 ReLU 之间图像的对比：

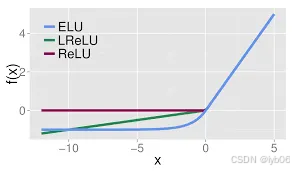
优点：

没有 Dead ReLU 问题，输出的平均值接近 0，以 0 为中心。
比 ReLU 系列有更平滑的曲线，输出更接近零中心化，可能获得比 ReLU 更好的分类准确率。

缺点：

计算涉及指数，比 ReLU 慢。

与 Leaky ReLU 类似，尽管理论上比 ReLU 要好，但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。

1.7 Swish函数

Swish激活函数又叫作自门控激活函数，它由 Google 研究人员提出。它是一个平滑、非单调的函数。在一些实验中被证明其性能略优于 ReLU，尤其是在更深的模型中。它像一个“自动门”，根据输入大小平滑地在0和输入值之间切换。

公式：

$\mathrm{Swish}(x) = x * \mathrm{sigmoid}(x)$

图像：

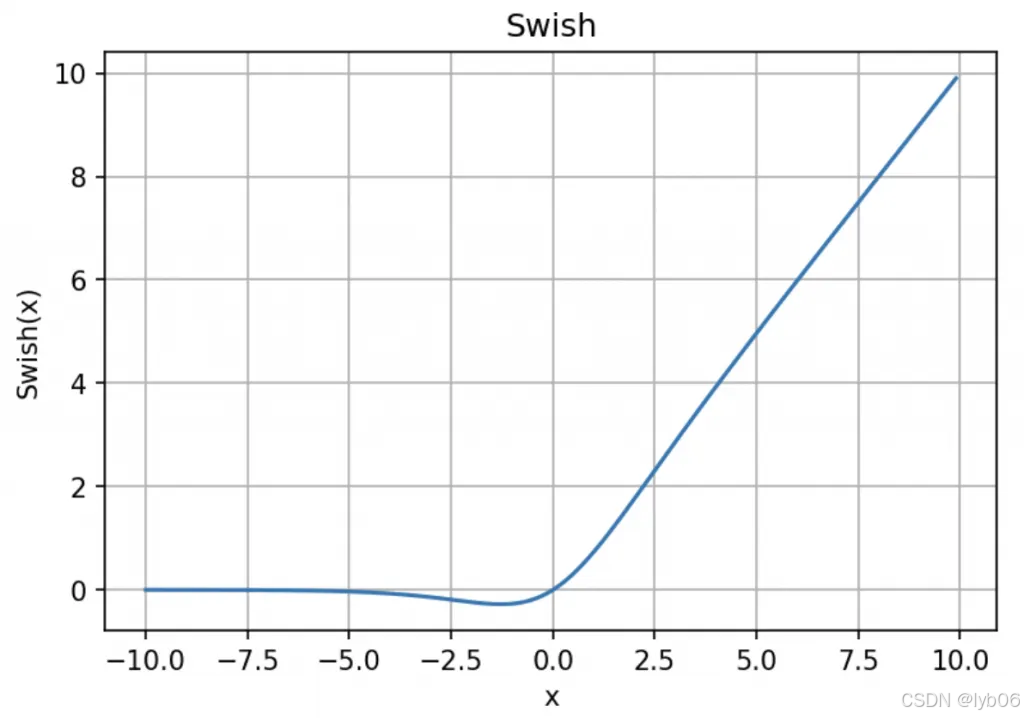
优点：

无界性有助于防止慢速训练时梯度逐渐接近0，造成饱和。
导数恒大于 0。
平滑度在优化和泛化中也起着重要作用。

1.8 Softsign函数

Softsign 函数是 Tanh 函数的另一个替代选择。就像 Tanh 函数一样，Softsign 函数是反对称、去中心、可微分，并返回 -1 和 1 之间的值。

公式：

$\mathrm{Softsign}(x)=\frac{x}{1+|x|}$

它的导数：

$\mathrm{Softsign'}(x)=\frac{1}{(1+|x|)^2}$

值域： [-1,1]

Softsign 函数及其导数的图像：

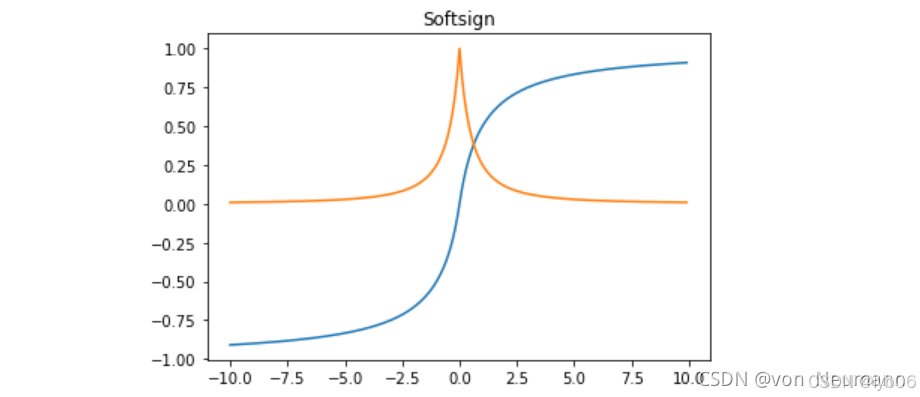
优点：

缓解梯度消失（Vanishing Gradient）的效果优于 Tanh 函数。从其导数公式可以看出，当增大时，其导数的衰减速度是多项式级的。而 Tanh 的导数是指数级衰减的。
输出是零中心化的（Zero-Centered）。
计算相对简单。虽然不如 ReLU 函数简单，但是其计算成本通常低于 Tanh 和 Sigmoid。

缺点：

仍未彻底解决梯度消失问题。
计算效率仍不如 ReLU。

1.9 Softmax函数

Softmax 是用于多类分类问题的激活函数，在多类分类问题中，超过两个类标签则需要类成员关系。Softmax 是一种特殊的激活函数，通常只用在多分类网络的输出层。它接收一个向量，然后将每个元素压缩到 (0,1) 之间，并且所有元素之和为 1。这样，它的输出可以直接解释为每个类别的概率分布。

公式：

$Softmax(x) = \frac{e^{x_i}}{\sum_i e^{x_i}}$

输入输出示例：

可以将网络的输出映射为概率值

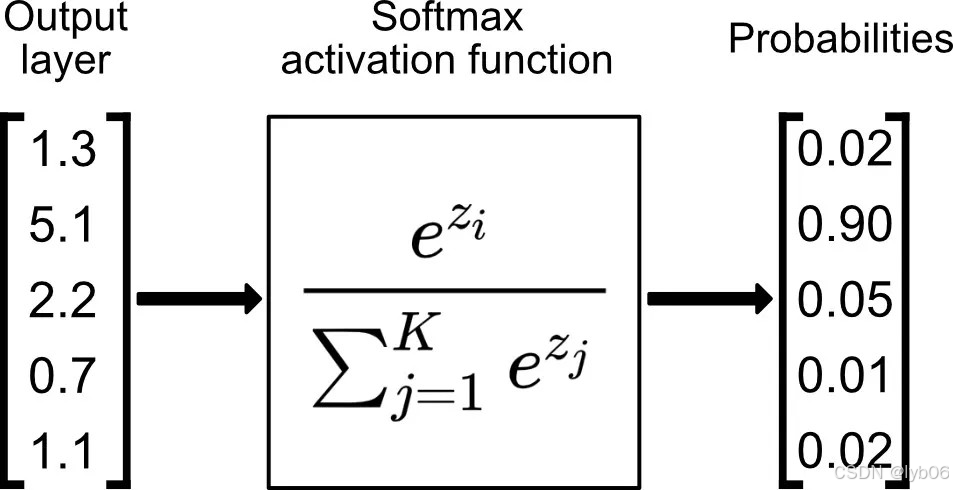
Softmax 与正常的 max 函数不同：max 函数仅输出最大值，但 Softmax 确保较小的值具有较小的概率，并且不会直接丢弃。我们可以认为它是 argmax 函数的概率版本或「soft」版本。

2、激活函数的选择

网络输出层的选择：

二分类问题：Sigmoid 函数
多分类问题：Softmax 函数
回归问题：通常不使用激活函数，或者在输出恒为正时使用 ReLU。

网络隐藏层的选择：

默认首选： ReLU。因为它简单、高效，在大多数情况下表现良好。
如果担心 “Dying ReLU” 问题，可以尝试 Leaky ReLU 或 ELU。
对于非常深的网络，可以尝试 Swish。

常用激活函数的总结：

激活函数	公式	优点	缺点	适用场景
Sigmoid	$\frac{1}{1+e^{-x}}$	输出平滑，适合概率	梯度消失，非零中心，计算慢	输出层（二分类）
Tanh	$\frac{e^x - e^{-x}}{e^x + e^{-x}}$	零中心化	梯度消失	隐藏层（较少用）
ReLU	$max(0, x)$	计算快，缓解梯度消失	神经元死亡，非零中心	隐藏层（最常用）
Leaky ReLU	$max(\alpha x, x)$	缓解神经元死亡问题	效果不稳定	隐藏层
Softmax	$\frac{e^{x_i}}{\sum_j e^{x_j}}$	输出概率分布	仅用于输出层	输出层（多分类）