线程间Bug检测工具Canary

1.Introduction

主要做跨线程value-flow bug检查，下面代码中两个函数中存在指向关系：1. $x\to o_1$, $b\to o_2$ 以及赋值关系: $o_1=a$。考虑跨线程的数据流存在 $y=x$、$o_1=b$（覆盖掉 $a$）。如果 ${\theta }_1$ 满足，那么 $o_1=a$，因此 $c=a$，print 操作安全。如果 ${\theta }_2$ 满足，那么线程执行完后根本不会执行 print 操作，因此没有bug。但是现有静态分析工具可能会错误判断 free(b) 到 print(*c) 存在use-after-free。

作者提出了Canary，对上面代码可构造如下value-flow graph，其中 $b@l_{13}\to c@l_6$ 对应 *y = b 和 c = *x，x, y 都指向了共同的堆对象 $o_1$，路径条件为 ${\theta }_1\wedge \neg {\theta }_1$。同时线程间执行需要保证语句的先后顺序，用 $O_2>O_1$ 表示 $l_2$ 在 $l_1$ 后执行，那么还存在偏序关系 $O_{13}>O_3\wedge O_{14}>O_3$。随后Canary会调用SMT求解上面约束条件验证该bug存在条件不可行。

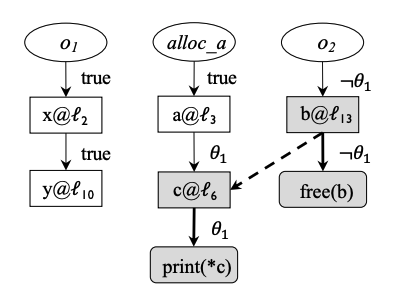
相比顺序程序，并发程序分析的核心在于，对于 $l_1:\ast x=q$, $l_2:p=\ast y$，不仅要分析 $x,y$ 别名的路径条件；还要分析 $l_1\to l_2$ 路径下 $x,y$ 可能指向的内存是否会被其它线程覆写。

2.Approach

分为数据依赖分析和线程间依赖分析。

2.1.数据依赖分析

规则如下和pinpoint类似，自底向上对每个函数生成summary再分析其caller，先进行代码转换方便暴露每个函数的side-effect。转换的规则应该覆用了pinpoint的，对于下面代码。

int f(v1, v2, ...) {...return v0;
}

转换后可能为：

int f(v1, v2, ... , F1, F2, ...) {∗(vj, k) = Fi; /* for all (i, j, k). */...;Rp = ∗(vq,r); /* for all (p,q,r). */return {v0, R1, R2, ...};
}

对于调用点:

// 转换前
u0 = f(u1, u2, ...);
// 转换后
Ai = ∗(uj, k); /* for all (i, j, k). */
{u0, C1, C2, ... } = f(u1, u2, ... ,A1,A2, ...);
∗(uq,r) = Cp =; /* for all (p,q,r). */

在分析函数 $F$ 时按照每个指令在CFG中的逆后序处理每条指令。分析完后 $\text{Trans}(F)$ 记录了 $F$ 在其形参 $v_i$ 的副作用。

线程内指令的分析规则基于flow-, path-sensitive指针分析，如下所示。这里暂时不考虑线程间的关系，碰到 fork 调用直接跳过。

指令类型	示例	规则
alloca	$l,\phi :p=\&o$	$(\phi ,o)\in \text{pts}(p)$
copy	$l,\phi :p=q$	$(\gamma \wedge \phi ,o)\in \text{pts}(p)\mid \forall (\gamma ,o)\in \text{pts}(q)$
load	$l,\phi :p=\ast y$	$(\gamma \wedge \phi ,o^{{}^{\prime }})\in \text{pts}(p)\mid \forall (\_,o)\in \text{pts}(y),\forall (\gamma ,o^{{}^{\prime }})\in {\text{pts}}_{{\text{IN}}_l}(o)$
store	$l,\phi :\ast x=q$	(1). $\text{pts}(x)=\varnothing \mid x\to (\gamma ,o)$ (strong update), (2).$(\gamma \wedge \phi ,o)\in \text{pts}(o^{{}^{\prime }})\mid \forall (\gamma ,o)\in \text{pts}(q),\forall ({\gamma }^{{}^{\prime }},o^{{}^{\prime }})\in \text{pts}(x)$
call	$l,\phi :(x_0,...,x_n)=f(v_1,...,v_n)$	$(\phi ,\text{Trans}(f,\text{pts}(v_i)))\in \text{pts}(x_i)\mid \forall i\in [1,n]$

2.2.线程间依赖分析

这一步是Canary的核心，当 $l_1:\ast x=q$ 和 $l_2:p=\ast y$ 在不同线程时，$x,y$ 别名的前提除了本身必须可能指向同一块内存外还必须满足 $O_2>O_1$，这步包括依赖边构造和依赖条件计算两个步骤。

2.2.1.依赖边构造

需要识别线程共享内存，这些内存对象被称为escaped memory。用 $\text{EspObj}$ 表示程序中所有escaped memory object，$\text{Pted}(o)$ 表示指向 $o$ 的所有指针。在线程内数据依赖分析基础上，作者定义下面规则，其中$t$ 表示某个线程，$t^{{}^{\prime }}$ 表示其它线程。

• 计算 $\text{EspObj}$：

  • step 1: 将 fork 调用中传递的object添加进 $\text{EspObj}$ 。

  • step 2: 根据已有的 $\text{EspObj}$ 和 store 指令更新集合，$o^{{}^{\prime }}\in \text{EspObj}\mid (c1).\forall l:\ast x=q(c2){(}_{,}o)\in \text{pts}(x){(}_{,}{o}^{{}^{\prime }})\in \text{pts}(q)(c3)o\in \text{EspObj}$。

• 计算 $\text{Pted}$: 对$\text{EspObj}$ 中的每个 $o$ 找到能传播到的所有指针，存入集合 $N$，$\sigma$ 为遍历过程中的路径条件：$(n,\sigma )\in \text{Pted}(o)$。

• 计算依赖边：: $l_1\to l_2\mid (c1).\forall l_1,{\phi }_1:\ast x=q\in t(c2).\forall l_2,{\phi }_2:p=\ast y\in t^{{}^{\prime }}(c3).(x,\alpha ),(y,\beta )\in \text{Pted}(o),(c4).o\in \text{EspObj}$。

这个示例中 EspObj={o1,o2}\text{EspObj} = \{o_1, o_2\}EspObj={o1​,o2​}, Pted(o1)={x,y}\text{Pted}(o_1) = \{x, y\}Pted(o1​)={x,y}, Pted(o2)={b,c}\text{Pted}(o_2) = \{b, c\}Pted(o2​)={b,c}（paper中这么写的，有点迷惑，fact的路径条件应该是被忽略了）。

2.2.2.依赖条件计算

一个value-flow edge: $l_1,{\phi }_1:\ast x=q⟶l_2,{\phi }_2:p=\ast y$ 的路径条件包括 $x,y$ 的别名条件 ${\Phi }_{\text{alias}}$ 以及 $O_2>O_1$ 的条件 ${\Phi }_{\text{ls}}$。

${\Phi }_{\text{alias}}=\bigvee ({\phi }_1\wedge {\phi }_2\wedge \alpha \wedge \beta )\mid \forall (\alpha ,o)\in \text{pts}(x),(\beta ,o)\in \text{pts}(y)$，上面示例中：*y = b -> c = *x 的条件为 ${\theta }_1\wedge \neg {\theta }_1$。

${\Phi }_{\text{ls}}$ 的计算中需要保证 (1) store s 和 load l 的执行顺序 $O_l>O_s$，同时 (2) $s\to l$ 之间没有其它 store 语句会写入 $o$。让 $S(l)$ 表示 $l$ 数据依赖的所有 store 语句。那么 ${\Phi }_{\text{ls}}=\underset{s,s^{{}^{\prime }}\in S(l)}{\bigwedge }(O_s<O_l\underset{\forall s^{{}^{\prime }}\ne s}{\bigwedge }{O}_{s^{{}^{\prime }}}<O_s\vee O_l<O_{s^{{}^{\prime }}})$。 $O_{s^{{}^{\prime }}}<O_s\vee O_l<O_{s^{{}^{\prime }}}$ 表示 $s$ 和 $l$ 之间不存在其它 store 语句会修改 $l$ 引用的内存。

3.Bug检测

这里主要检测线程间use after free。其中source为 free 点，sink为 use 点。其中存在source - sink路径 $\pi =⟨v_1@l_1,v_2@l_2,...,v_k@l_k⟩$，bug存在的条件 ${\Phi }_{\text{all}}(\pi )={\Phi }_{\text{guards}}(\pi )\wedge {\Phi }_{\text{po}}(\pi )$。

• ${\Phi }_{\text{guards}}(\pi )=\underset{i\in [1,k-1]}{\bigwedge }{\Phi }_{\text{guards}}(v_i@l_i\to v_{i+1}@l_{i+1})$ 为数据依赖的路径条件。

• ${\Phi }_{\text{po}}(\pi )=\underset{i\in [1,k-1]}{\bigwedge }\underset{j\in [i,k-1]}{\bigwedge }{\Phi }_{\text{po}}(v_i@l_i\to ...\to v_j@l_j)$ 为语句偏序关系约束。

4.Evaluation

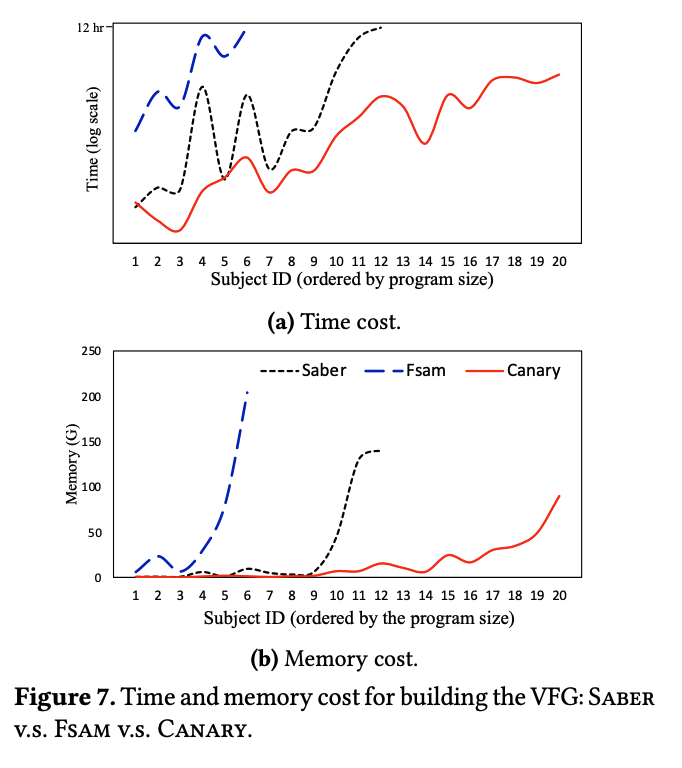
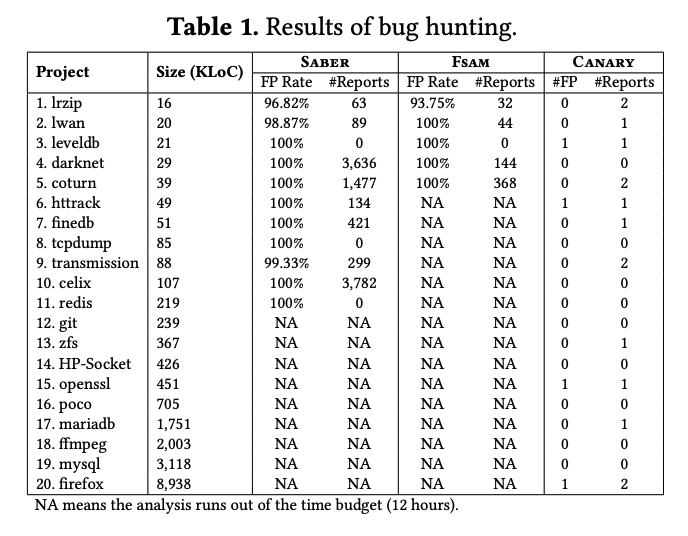
和FASM以及Saber进行了比较，采用了20个开源程序进行评估。

参考文献

[1].Yuandao Cai, Peisen Yao, and Charles Zhang. 2021. Canary: practical static detection of inter-thread value-flow bugs. In Proceedings of the 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation (PLDI 2021). Association for Computing Machinery, New York, NY, USA, 1126–1140. https://doi.org/10.1145/3453483.3454099