损耗源:导线电阻与趋肤效应
损耗源:导线电阻与趋肤效应:
在信号路径和返回路径中,信号受到的串联电阻与导线的体电阻率和电流传播通过的横截面有关。直流时,电流在信号导线中均匀分布,电阻为
其中,R表示传输线的电阻(单位为Ω),表示导线的体电阻率(单位为
·in),Len表示线长(单位为in),
表示线宽(单位为in),t表示导线的厚度(单位为in)。
如果返回路径是一个平面,则直流电流分布就在横截面上扩展开,且返回路径电阻比信号路径电阻小得多,可以忽略不计。
典型的5mil宽、1.4mil厚(1盎司铜)的1in长的铜导线,其信号路径的直流电阻约为R=0.72xΩ·inx1 in/(0.005 x0.0014)=0.1 Ω。
在频率接近100GHz之前,铜和其他所有金属的体电阻率完全是个常数,与频率无关。乍看起来,可能认为线电阻也许是与频率无关的常量,这仅是理想电阻器的性能。正如前面章节中讲到的,由于趋肤效应的影响,电流在高频时将重新分布。
高频时,铜导线中电流经过的横截面厚度约等于集肤深度,即

其中,表示集肤深度(单位为
),f表示正弦波频率(单位为GHz)。
1CHz时,微带线信号路径铜线中电流的每一面的集聚厚度约为2.1μm。10MHz时,即0.01GHz时,集聚厚度约为21μm。这是粗略的近似,通常用二维场求解器计算信号路径和返回路径中的实际电流分布。图9.6为10MHz正弦波在微带线和带状线中的电流分布示例。
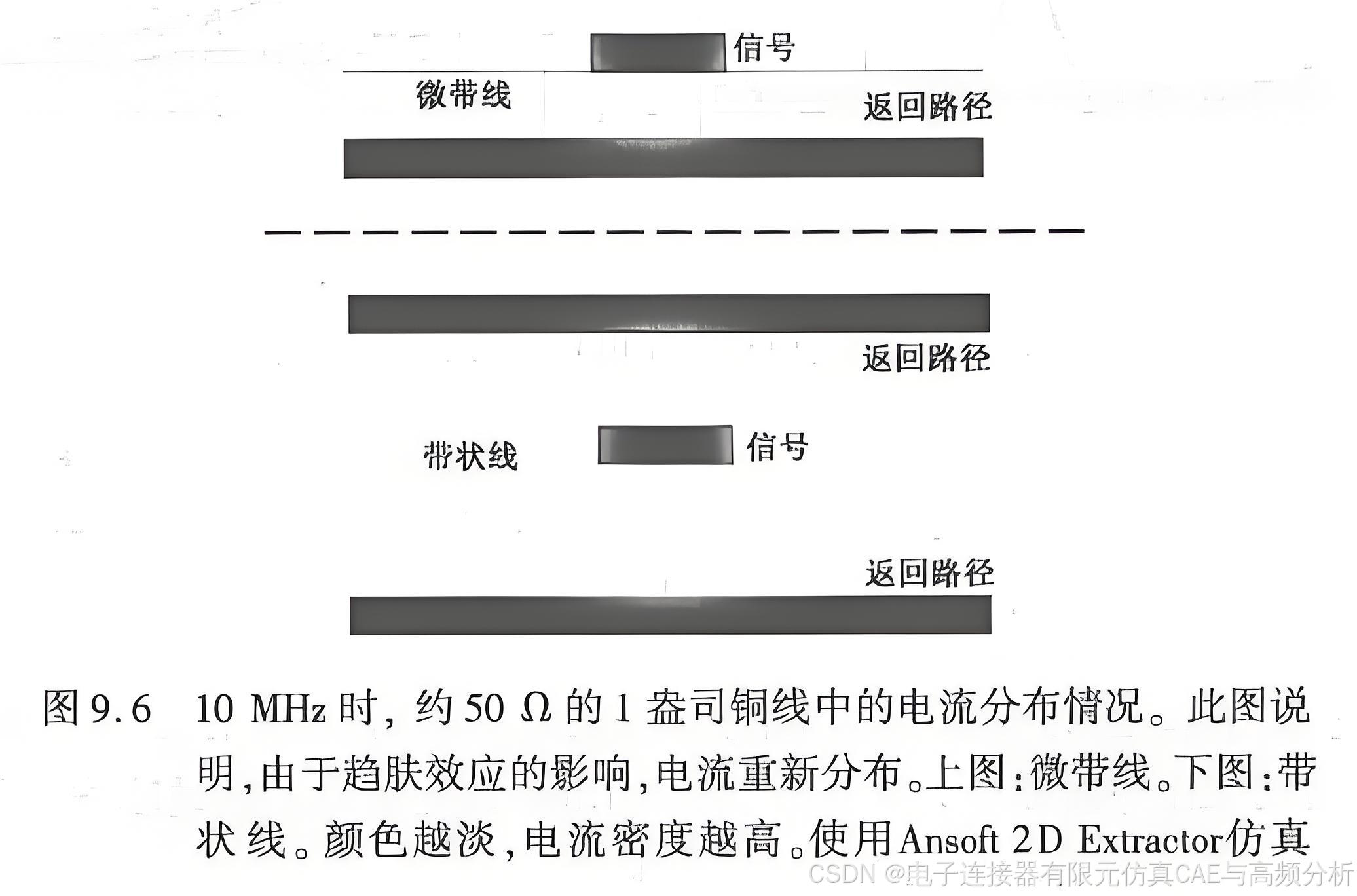
对于1盎司铜,它的几何厚度为35um。频率高于10MHz时,集肤深度小于厚度。电流的分布取决于电流总是寻求最小阻抗的路径,即频率更高时,寻找回路电感最低的路径。这体现为两种趋势:导线中的电流都尽可能地扩展开,以使导线的自感最小:同时导线中的反向电流尽可能地挤近,以使这两个电流之间的互感最大。
提示,显然,对于信号的所有重要频率分量,多数PCB互连中的电流分布总是受限于集肤深度。对于大于10MHz的频率分量,电阻与频率有关。
信号感受到的电阻取决于导线传输电流的有效横截面。频率越高,电流流经的导线横截面就越小,电阻随着频率的升高而增加。与频率有关的趋肤效应使电阻随频率变化。但要注意,当频率变化时,铜和大多数金属的电阻率是相当恒定的,所变化的是电流流过的横截面大约在10MHz以上时,信号路径单位长度电阻是与频率有关的。由于趋肤效应,如果电流仅流过导线的下半部分,则导线的电阻近似为
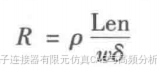
其中,R表示线电阻(单位为Ω),表示导线的体电阻率(单位为
·in),Len 表示线长(单位为in),w表示线宽(单位为in),
表示导线的集肤深度(单位为in)。
正如前面图中看到的,即使在微带线中,电流也不仅仅流经导线的下半部分。在导线的上半部分中也有相当多的电流,这两个区域是平行的。考虑到信号路径中的这两条平行路径,信号路径的电阻近似为0.5R。微带线和带状线信号路径中的电流分布非常相似。
趋肤效应是由电流流经最低阻抗路径的要求促成的,而在高频中,路径的阻抗主要由回路电感决定。这种机理也驱使电流在返回路径中重新分布,并随频率而变化。直流时,返回电流分布在整个返回平面上。在趋肤效应的制约下,返回路径中的电流将挤近分布在靠近信号路径的表面上,这样可以使回路电感最小。
如前面图9.6所示,微带线的返回路径中电流分布的宽度约等于信号路径宽度的3倍。返回路径的电阻与信号路径的电阻是串联的,所以在频率高于10 MHz时,传输线的总电阻为0.5R+0.3R=0.8R,即微带线信号路径的总电阻预计约为

其中,R表示线电阻(单位为Ω),表示导线的体电阻率(单位为
·in),Len表示线长(单位为in),w表示线宽(单位为in),
表示导线的集肤深度(单位为in).0.8表示系数,由信号路径和返回路径中的具体电流分布确定。
图9.7将这个简单的一阶模型与二维场求解器的计算结果进行比较,其中二维场求解器计算出了每一频率点的精确电流分布。对于这个简单模型而言,从低频区到趋肤效应作用频段,吻合得都非常好。从图9.7中可以看出,带状线单位长度电阻要稍微低一些。
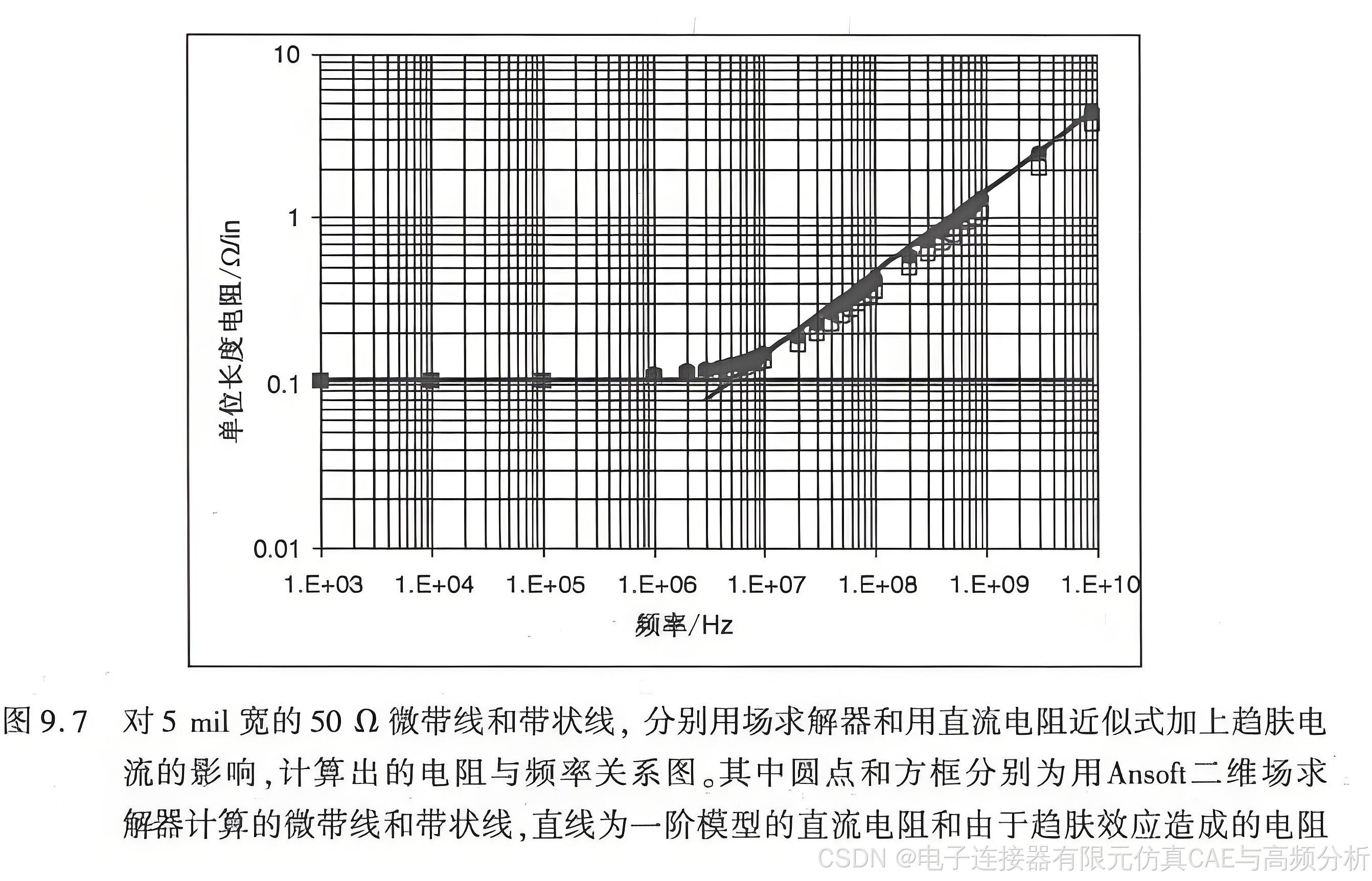
我们的结论是,传输线中的导线串联电阻随着频率的升高而增加。至于与频率有关的电阻怎样影响损耗,将在本章后面讨论。
