人工智能之数学基础：事件独立性

本文重点

在概率论与统计学中，事件独立性是构建概率模型的基础概念之一。它不仅简化了复杂事件的概率计算，更是统计学推断、机器学习算法（如朴素贝叶斯）的核心假设。

定义

如果P(B|A)=P(B)，或者P(A|B)=P(A)，则可以认为事件A并不会影响到事件B，专业术语是事件A和事件B独立。如果事件A和事件B独立，那么P(A,B)=P(A)P(B)

示例：

抛掷一枚均匀硬币两次，事件A="第一次正面朝上"，事件B="第二次反面朝上"。由于两次抛掷结果互不影响，显然：

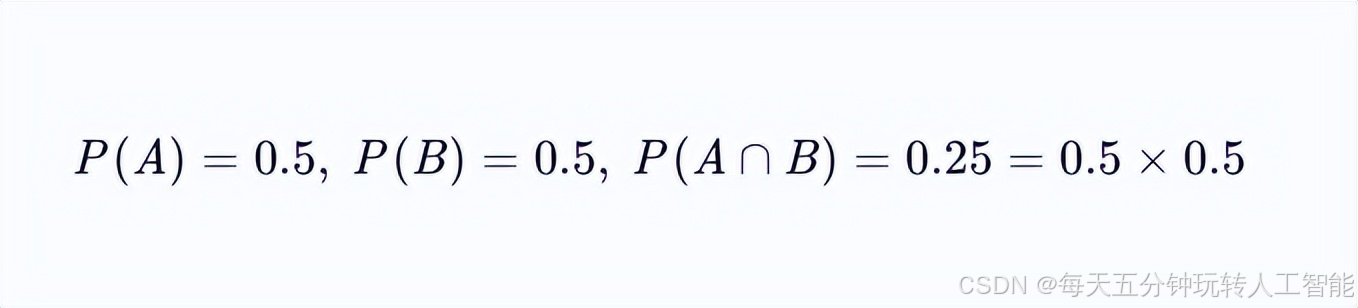
符合独立性的定义。

事件独立性推广

如果n个随机事件Ai，...,An相互独立，则有：

P(A1,A2,...,An)=P(A1)P(A2)...P(An)

注意：

多事件独立性要求所有子集满足乘积关系，而不仅仅是两两独立。例如，三个事件两两独立未必整体独立。

事件独立性的核心性质

独立事件与互斥事件的区别：

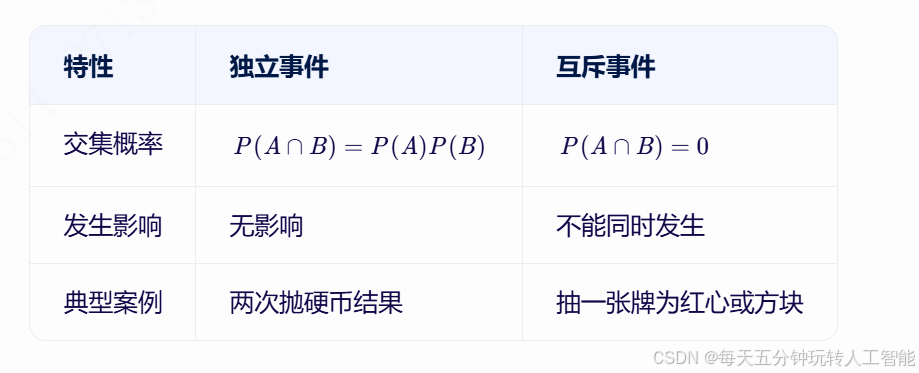
独立事件的运算规则

和事件概率：<