凸优化理论记录

1. 共轭函数

1.1 定义

一个函数 f 的共轭函数(conjugate function) 定义为

  是凸函数，证明也很简单，可以看成是一系列关于 y 的凸函数取上确界。

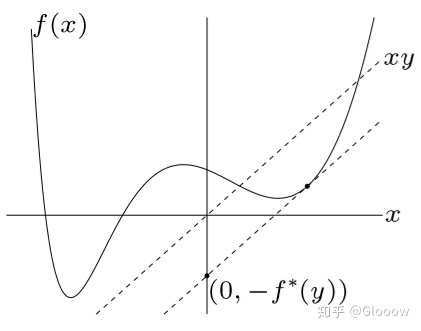
Remarks：实际上共轭函数与前面讲的一系列支撑超平面包围 f 很类似，通过 y 取不同的值，也就获得了不同斜率的支撑超平面，最后把 f 包围起来，就好像是得到了   的一个闭包，如下图所示

1.2 性质

关于共轭函数有以下性质

1. 若 f 为凸的且是闭的(   为闭集)，则   (可以联系上面提到一系列支撑超平面)
2. (Fenchel's inequality)   ，这可以类比均值不等式
3. (Legendre transform)如果   ，且为凸的、闭的，设  ，那么有  。这可以用来求极值，比如  

1.3 例子

常用的共轭函数的例子有

负对数函数  

凸二次函数  with  

指示函数  on  

log-sum-exp 函数 

范数  

范数平方  

负熵  

矩阵特征值对数