当前位置：首页 > ds >正文

力扣：2458. 移除子树后的二叉树高度（dfs序）

ds 2025/9/5 1:01:16

给你一棵 二叉树 的根节点 root ，树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。

你必须在树上执行 m 个独立的查询，其中第 i 个查询你需要执行以下操作：

从树中移除以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不等于根节点的值。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是执行第 i 个查询后树的高度。

注意：

查询之间是独立的，所以在每个查询执行后，树会回到其初始状态。
树的高度是从根到树中某个节点的 最长简单路径中的边数 。

示例 1：

输入：root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出：[2]
解释：上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2（路径为 1 -> 3 -> 2）。

示例 2：

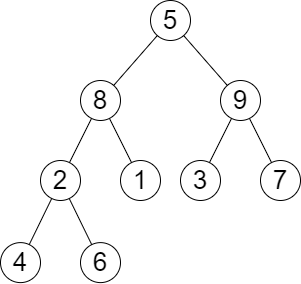
输入：root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
输出：[3,2,3,2]
解释：执行下述查询：
- 移除以 3 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 4）。
- 移除以 2 为根节点的子树。树的高度变为 2（路径为 5 -> 8 -> 1）。
- 移除以 4 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 6）。
- 移除以 8 为根节点的子树。树的高度变为 2（路径为 5 -> 9 -> 3）。

提示：

树中节点的数目是 n
2 <= n <= 105
1 <= Node.val <= n
树中的所有值 互不相同
m == queries.length
1 <= m <= min(n, 104)
1 <= queries[i] <= n
queries[i] != root.val

最初的思路很简单：

一遍 dfs 走完全程，枚举 queries里面的所有元素 i，在 i 结点被删除的情况下考虑最长路径。每一次枚举，dfs都从根节点出发向下搜索，先走左子树，再走右子树，每次向下搜索时都将深度+1，如果在搜索的过程中遇到了当前删除的结点 i 就回溯，直到当前结点不可向下 (一个子树为空，另一个子树为当前被删除，) 或者当前结点为叶子结点 (左右子树都为空)，搜索停止，判断当前深度是否为最大，然后return回溯。然而 35/40 时间超限。

参考代码：

class Solution {
public:vector<int> ans;vector<int> treeQueries(TreeNode* root, vector<int>& queries) {for (auto it : queries) {ans.push_back(0);if (it == root->val) {//删除的结点为根节点continue;}else {if (root->left != nullptr && root->left->val != it) {//左子树不空且左子树的节点值与删除的结点值不等dfs(root->left, 1, it);}if (root->right != nullptr && root->right->val != it) {//右子树不空且右子树的节点值与删除的结点值不等dfs(root->right, 1, it);}}}return ans;}void dfs(TreeNode* x, int sum,int re) {if (x->left == nullptr && x->right == nullptr) {//到达叶子结点int k = ans.back();if (sum > k) {ans.pop_back();ans.push_back(sum);}return;}else if ((x->left == nullptr && x->right->val == re) || (x->right == nullptr && x->left->val == re)) {// 未到达叶子结点但不可向下int k = ans.back();if (sum > k) {ans.pop_back();ans.push_back(sum);}return;}else {if (x->left != nullptr && x->left->val != re) {//左子树不空且左子树的节点值与删除的结点值不等dfs(x->left, sum + 1, re);}if (x->right != nullptr && x->right->val != re) {//右子树不空且右子树的节点值与删除的结点值不等dfs(x->right, sum + 1, re);}}}
};

接下来就是思考如何优化时间的问题：

在上述的代码中树上结点数n如果=1e5，queries 数组长度如果达到1e4，那么时间复杂度无疑是极大的。

而换一种想法，将某棵子树删除后求最大路径，就等同于在剩下的树中求最大深度。而将子树删除就等同于将子树上所有的结点标记，那么就需要2次 dfs，第一次dfs获取所有结点的深度并记录在dep数组中，然后枚举 queries数组中的元素 i，第二次 dfs搜索以 i 结点为根的子树，将子树上的所有结点标记，标记完成后遍历 dep数组，在未标记的dep数组中找出最大深度。

然而依旧时间超限。。。

参考代码：

class Solution {
public:vector<int> ans;static const int N = 1e5 + 10;int dep[N];//每个结点的深度bool flag[N];int n = 0;map<int, TreeNode*> mp;vector<int> treeQueries(TreeNode* root, vector<int>& queries) {dfs(root,0);//确定每个结点对应的深度for (auto it : queries) {memset(flag, 0, sizeof flag);dfs(mp[it]);int k = 0;for (int i = 1;i <= n;i++) {// 遍历所有结点的深度if (!flag[i]) {//在未标记的结点中找最大深度k = max(k, dep[i]);}}ans.push_back(k);}return ans;}void dfs(TreeNode* x, int sum) {dep[x->val] = sum;mp[x->val] = x;n++;if (x->left == nullptr && x->right == nullptr) {return;}else{if (x->left != nullptr) {dfs(x->left, sum + 1);}if (x->right != nullptr) {dfs(x->right, sum + 1);}}}void dfs(TreeNode* x) {flag[x->val] = 1;if (x->left == nullptr && x->right == nullptr) {return;}else {if (x->left != nullptr) {dfs(x->left);}if (x->right != nullptr) {dfs(x->right);}}}

再对上述代码进行分析：

树上结点数n如果=1e5，queries 数组中的元素如果都比较接近根节点，那么每次标记所走的 dfs其时间复杂度同样很大，在时间上并不会很占优。

然而写到这里就不难发现，上述代码中所删除的子树在 dfs序中无疑是一个整体，如果这时候通过dfs获取整棵树的 dfs序再通过一维数组将 dfs序罗列出来，我们想删除的子树实际上就是这个一维数组上的一个片段。举例如下图：

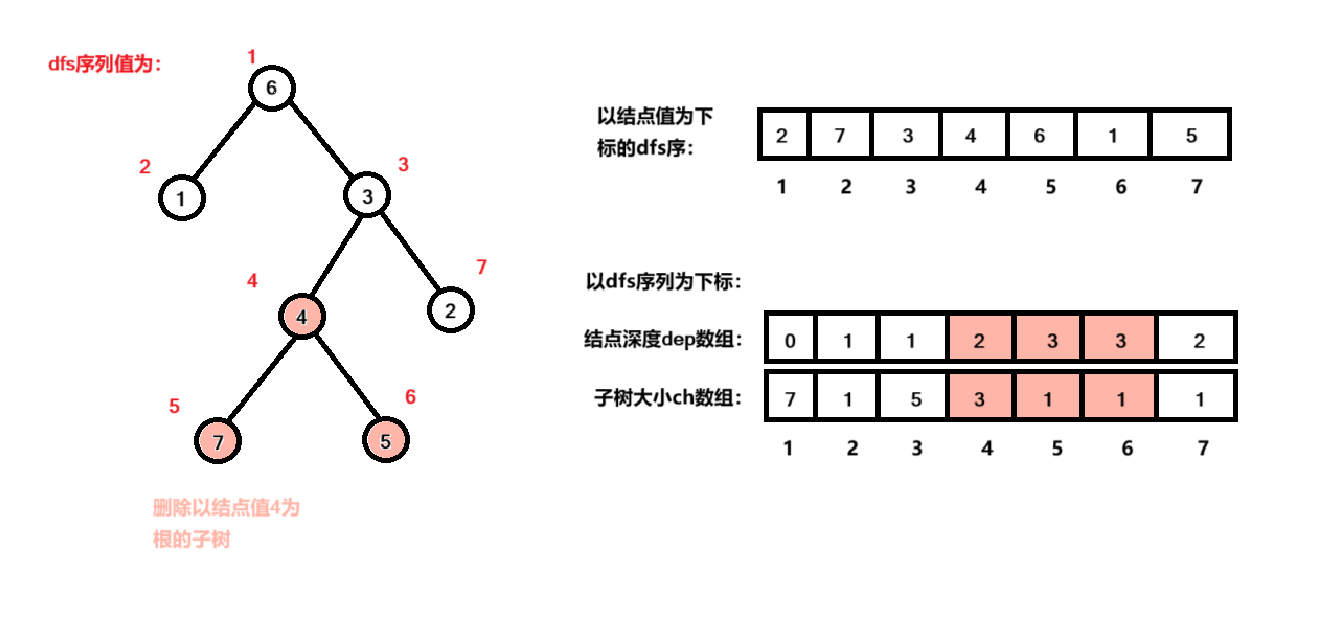
将片段删除后，整个一维数组就剩下左右两段。如果此时我们将上述代码获取到的 dep数组改写一下：原本dep数组表示结点值为 i 其对应深度，改写成 dfs序号为 i 的结点深度；将dep数组与dfs序数组对应起来，那么此时的最长路径就是在 dfs序的一维数组剩下的左右两侧中找最大深度。

在最后找最大深度时建议使用前后缀比大小，线性遍历dep数组会时间超限。

AC代码：

C++版：

class Solution {
public:static const int N = 1e5 + 10;int dep[N];//dfs序号为i的节点的深度int dfn[N];//第i个节点的dfs序号int ch[N];//以dfs序号为i的节点的子树大小int n = 1;int suf[N];//后缀最大值int pre[N];//前缀最大值vector<int> ans;vector<int> treeQueries(TreeNode* root, vector<int>& queries) {ch[1] = dfs(root, 0);//构建前缀最大值数组pre[0] = 0;for (int i = 1;i < n;i++) {pre[i] = max(pre[i - 1], dep[i]);}//构建后缀最大值数组suf[n] = 0;for (int i = n - 1;i >= 1;i--) {suf[i] = max(suf[i + 1], dep[i]);}for (auto it : queries) {//处理查询int l = dfn[it];int r = l + ch[l] - 1;int k = max(pre[l - 1], suf[r + 1]);ans.push_back(k);}return ans;}int dfs(TreeNode* x, int sum) {if (x == nullptr) {return 0;}dfn[x->val] = n;dep[n] = sum;int idx = n;n++;int l = dfs(x->left, sum + 1);int r = dfs(x->right, sum + 1);ch[idx] = l + r + 1;return ch[idx];}
};

java版本：

import java.util.ArrayList;class Solution {static final int N=100010;ArrayList<Integer> arr=new ArrayList<>();int ch[]=new int[N];int dfn[]=new int[N];int dep[]=new int[N];public int n=1;int pre[]=new int[N];int suf[]=new int[N];public int[] treeQueries(TreeNode root, int[] queries) {ch[1]=dfs(root,0);pre[0]=0;for(int i=1;i<n;i++){pre[i]=Math.max(dep[i],pre[i-1]);}suf[n]=0;for(int i=n-1;i>=1;i--){suf[i]=Math.max(dep[i],suf[i+1]);}for(int i:queries) {int l = dfn[i];int r = l + ch[l] - 1;int k = Math.max(pre[l - 1], suf[r + 1]);arr.add(k);}int ans[]=arr.stream().mapToInt(Integer::intValue).toArray();return ans;}int dfs(TreeNode x,int sum){if(x==null){return 0;}dfn[x.val]=n;int idx=n;dep[idx]=sum;n++;int l=dfs(x.left,sum+1);int r=dfs(x.right,sum+1);ch[idx]=l+r+1;return ch[idx];}
}