当前位置：首页 > ds >正文

比随机森林更快更强？极限森林的核心逻辑与完整实践指南

ds 2025/8/30 14:22:12

前言

在机器学习领域，集成学习凭借 “多模型协同决策” 的思想，往往能显著提升模型的泛化能力，其中*随机森林（Random Forest）*是最经典的代表之一。

而极限森林（Extremely Randomized Trees，简称 Extra-Trees） 作为随机森林的 “进阶版”，通过进一步增强随机性，在某些场景下能避免过拟合、提升计算效率。

本文将从 “极限森林的随机性本质” 切入，系统讲解其核心原理，并结合Sklearn实战代码，对比单棵决策树、随机森林与极限森林的差异，帮助读者深入理解极限森林的设计逻辑与应用价值。

1、极限森林介绍

极限森林的核心设计理念是通过增强决策树构建过程中的随机性，减少模型间的相关性，从而进一步降低过拟合风险。与随机森林相比，它的“随机”体现在两个关键环节，且随机性更强。

要理解极限森林的随机特性，我们先通过表格对比它与随机森林、单棵决策树的核心差异：

模型	训练集抽样方式	特征选择方式（节点分裂时）	分裂阈值选择方式	核心优势
单棵决策树	全量训练集	所有特征中选择最优分裂特征	遍历特征所有可能阈值，选最优	可解释性强，训练速度快
随机森林	自助采样（Bootstrap）	随机抽样部分特征（默认 $n\sqrt{n}$ 个）	遍历抽样特征的可能阈值，选最优	泛化能力强，抗过拟合
极限森林	全量训练集	随机抽样部分特征（更灵活）	随机选择阈值，而非最优	随机性更强，计算更快，抗过拟合更优

1.1 极限森林的三大随机

极限森林，都有哪些随机？

极限森林中每一个决策树都采用原始训练集

随机森林构建每棵决策树时，会通过Bootstrap自助采样（有放回抽样）生成不同的训练子集，以此保证单棵树的多样性。

而极限森林的每一棵决策树，都直接使用原始全量训练集—— 它不依赖抽样来制造数据差异，而是通过后续“特征随机”和“阈值随机”来实现树的多样性。这种设计的好处是：避免了Bootstrap抽样可能导致的部分样本被重复使用、部分样本被遗漏的问题，同时减少了抽样环节的计算开销。

抽样后，分裂时，每一个结点分裂时，都进行特征随机抽样（一部分特征作为分裂属性）

与随机森林类似，极限森林在每个节点分裂时，会随机抽取一部分特征（而非全部特征）作为候选分裂特征。默认情况下，分类任务中抽取的特征数为√总特征数，回归任务中为总特征数/3（可通过max_features参数调整）。

这种“特征随机”的目的是：避免单棵树过度依赖“强特征”（如数据集中区分度极高的特征），从而减少树与树之间的相关性 —— 如果所有树都依赖同一强特征，集成后的模型会过度偏向该特征，反而降低泛化能力。

从分裂随机中筛选最优分裂条件

这是极限森林与随机森林最核心的区别，也是其“极限（Extremely）”一词的来源。

随机森林 / 单棵决策树：在候选特征中，会遍历该特征的所有可能分裂阈值（如对连续特征排序后，取相邻样本的均值作为候选阈值），选择使分裂后不纯度（如Gini系数、信息增益）最小的阈值（即“最优阈值”）。

极限森林：在候选特征中，会随机生成若干个分裂阈值（而非遍历所有可能），然后从这些随机阈值中选择一个相对较优的（如使不纯度下降最多的）作为分裂条件。

这种“阈值随机”的设计，进一步增强了单棵树的随机性，同时大幅减少了阈值遍历的计算量 —— 尤其当特征维度高、样本量大时，极限森林的训练速度会显著快于随机森林。

1.2 极限森林的优缺点总结

优点

更强的抗过拟合能力：通过 “阈值随机” 减少单棵树的拟合程度，同时降低树间相关性，集成后泛化能力更优。

更快的训练速度：无需 Bootstrap 抽样，且不遍历所有阈值，计算开销低于随机森林。

对噪声数据更鲁棒：随机性增强使其不易受数据中噪声的影响。

缺点

可解释性略低：相比随机森林，阈值的随机性导致单棵树的分裂逻辑更难解释。

可能欠拟合：若随机性过强（如max_features过小、随机阈值数量过少），可能导致单棵树拟合不足，集成后性能下降。

2、极限森林实战

本节将通过“葡萄酒分类任务”（Sklearn内置数据集），对比单棵决策树、随机森林与极限森林的性能，并可视化极限森林的单棵树结构，验证其“阈值随机”特性。

2.1、加载数据

首先导入所需库，并加载数据集。葡萄酒数据集包含178个样本、3个特征，目标是将葡萄酒分为3个类别（对应3种不同的葡萄酒产地）。

import warnings
warnings.filterwarnings('ignore')
import numpy as np
from sklearn.ensemble import RandomForestClassifier,ExtraTreesClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
import graphviz
from sklearn import tree# 加载数据
X,y = datasets.load_wine(return_X_y = True)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 119)

2.2、单棵决策树

clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
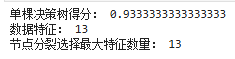
print('单棵决策树得分：',clf.score(X_test,y_test))
print('数据特征：',clf.n_features_in_)
print('节点分裂选择最大特征数量：',clf.max_features_)

2.3、随机森林

clf2 = RandomForestClassifier()
clf2.fit(X_train,y_train)
print('随机森林得分：',clf2.score(X_test,y_test))
print('数据特征：',clf2.n_features_)
for t in clf2:print('节点分裂选择最大特征数量：',t.max_features_)

2.4、极限森林

clf3 = ExtraTreesClassifier(max_depth = 3)
clf3.fit(X_train,y_train)
print('极限森林得分：',clf3.score(X_test,y_test))
print('数据特征：',clf3.n_features_)
for t in clf3:print('节点分裂选择最大特征数量：',t.max_features_)

2.5、可视化

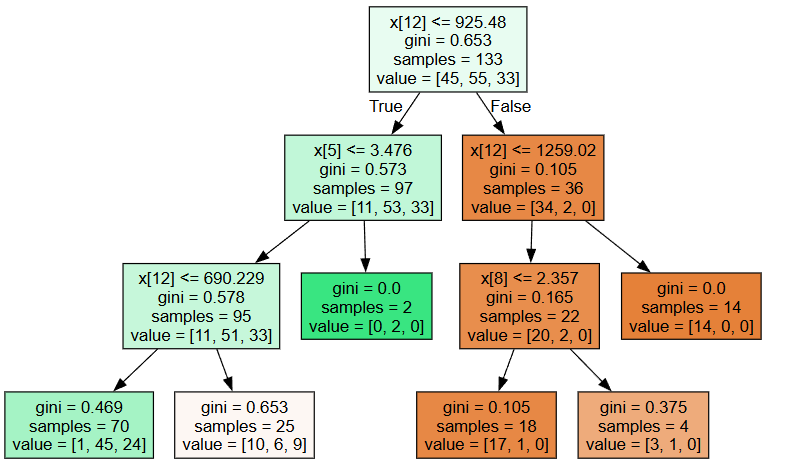
dot_data = tree.export_graphviz(clf3[0],filled=True)
graph = graphviz.Source(dot_data)
graph

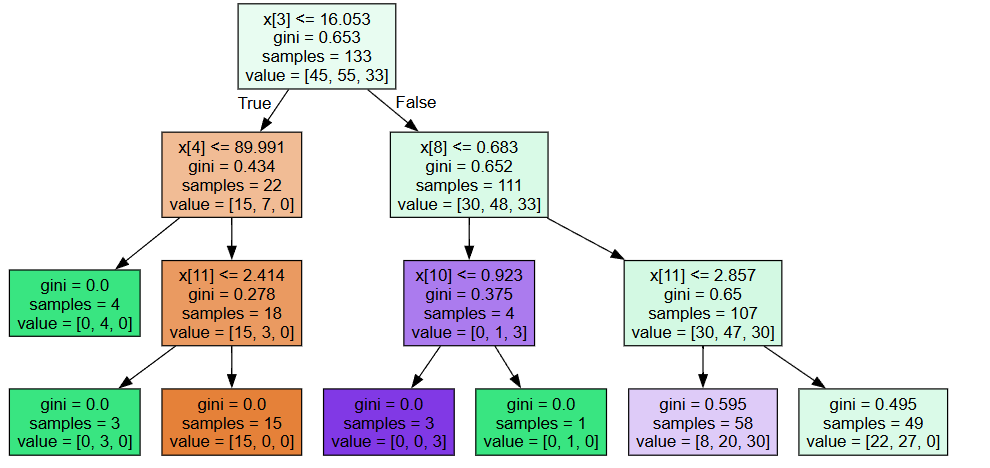
dot_data = tree.export_graphviz(clf3[49],filled=True)
graph = graphviz.Source(dot_data)
graph

2.6、分裂标准代码演练

为了深入理解极限森林的“随机分裂”特性，我们通过代码手动计算Gini系数，对比“最优分裂阈值”与极限森林实际选择的分裂阈值，验证其随机性。

2.6.1、计算未分裂gini系数

在进行特征分裂前，我们先计算整个训练集的Gini系数（不纯度），作为后续分裂的基准。

Gini系数的计算公式为：

$\sum_{i=1}^{k} p_i(1-p_i) = 1-\sum_{i=1}^{k} p_i^2$
其中， $p_i$ 是第 i 类样本在当前节点中的占比，k是类别总数。

# 统计训练集中每个类别的样本数量
count = []
for i in range(3):  # 葡萄酒数据集有3个类别count.append((y_train == i).sum())  # 计算类别i的样本数
count = np.array(count)  # 转换为数组，便于后续计算# 计算每个类别的占比
p = count / count.sum()  # 总样本数 = count.sum()# 计算Gini系数
gini = (p * (1 - p)).sum()  # 按公式计算print(f'未分裂时，Gini系数是：{round(gini, 3)}')

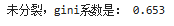
Gini系数的取值范围是 [0, 1]，0 表示节点中所有样本属于同一类别（纯度最高），1 表示类别分布最均匀（纯度最低）。

此处未分裂时 Gini 系数为 0.653，说明样本存在一定的类别混合，有分裂的必要。

2.6.2、根据属性寻找最佳分裂条件

接下来，我们以特征 11（根据前文特征重要性分析，该特征对分类影响较大）为例，遍历所有可能的分裂阈值，寻找使 Gini 系数最小的“最优分裂点”。

# 选择特征11（索引为11），并对该特征的取值进行排序
f = np.sort(X_train[:, 11])  # 排序后便于计算相邻样本的均值作为候选阈值gini_lower = 1  # 初始化最小Gini系数（初始值设为最大可能值1）
best_split = {}  # 用于存储最优分裂阈值# 遍历所有可能的分裂点（相邻样本的均值）
for i in range(len(f) - 1):# 计算相邻两个样本的均值作为候选分裂阈值split = round(f[i:i + 2].mean(), 3)# 根据阈值划分样本：小于等于阈值的为part1，否则为part2cond = X_train[:, 11] <= splitpart1 = y_train[cond]  # 左子节点样本part2 = y_train[~cond]  # 右子节点样本# 计算左子节点的Gini系数count1 = []for j in range(3):count1.append((part1 == j).sum())  # 统计左子节点中每个类别的数量count1 = np.array(count1)p1 = count1 / count1.sum() if count1.sum() > 0 else 0  # 避免除以0gini1 = round((p1 * (1 - p1)).sum(), 3)  # 左子节点Gini系数# 计算右子节点的Gini系数count2 = []for j in range(3):count2.append((part2 == j).sum())  # 统计右子节点中每个类别的数量count2 = np.array(count2)p2 = count2 / count2.sum() if count2.sum() > 0 else 0gini2 = round((p2 * (1 - p2)).sum(), 3)  # 右子节点Gini系数# 计算分裂后的整体Gini系数（加权平均）total_samples = y_train.sizegini = round(gini1 * (count1.sum() / total_samples) + gini2 * (count2.sum() / total_samples), 3)# 更新最优分裂点（保留Gini系数最小的阈值）if gini < gini_lower:gini_lower = ginibest_split.clear()best_split['阈值'] = splitbest_split['左子节点Gini'] = gini1best_split['右子节点Gini'] = gini2# 打印当前分裂点的详细信息（可选，用于调试）# print(f"分裂阈值: {split}, 左Gini: {gini1}, 右Gini: {gini2}, 整体Gini: {gini}")print(f"最优分裂条件: {best_split}")
print(f"分裂后最小Gini系数: {gini_lower}")