梯度下降(线性回归为例)
1.梯度下降
1.1梯度下降概念
正规方程求解的缺点
之前利用正规方程求解的W是最优解的原因是MSE这个损失函数是凸函数。但是,机器学习的损失函数并非都是凸函数,设置导数为0会得到很多个极值,不能确定唯一解,MSE还有一个问题,当数据量和特征较多时,矩阵计算量太大.
1.假设损失函数是这样的,利用正规方程求解导数为0会得到很多个极值,不能确定唯一解
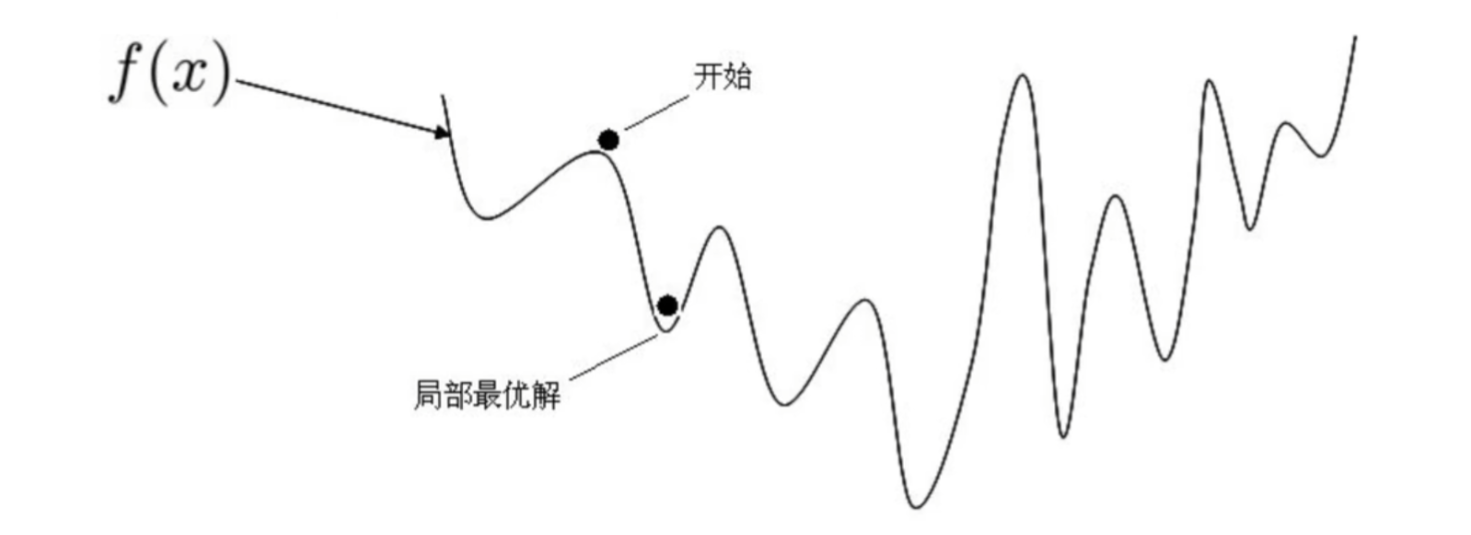
2.使用正规方程$W=(X^TX)^{-1}X^Ty$ 求解要求X的特征维度$(x_1,x_2,x_3...)$ 不能太多,逆矩阵运算时间复杂度为$O(n^3)$ , 也就是说如果特征x的数量翻倍,计算时间就是原来的$2^3$倍,8倍太恐怖了,假设2个特征1秒,4个特征8秒,8个特征64秒,16个特征512秒,而往往现实生活中的特征非常多,尤其是大模型,运行时间太长了
所以 正规方程求出最优解并不是机器学习和深度学习常用的手段,梯度下降算法更常用
什么是梯度下降
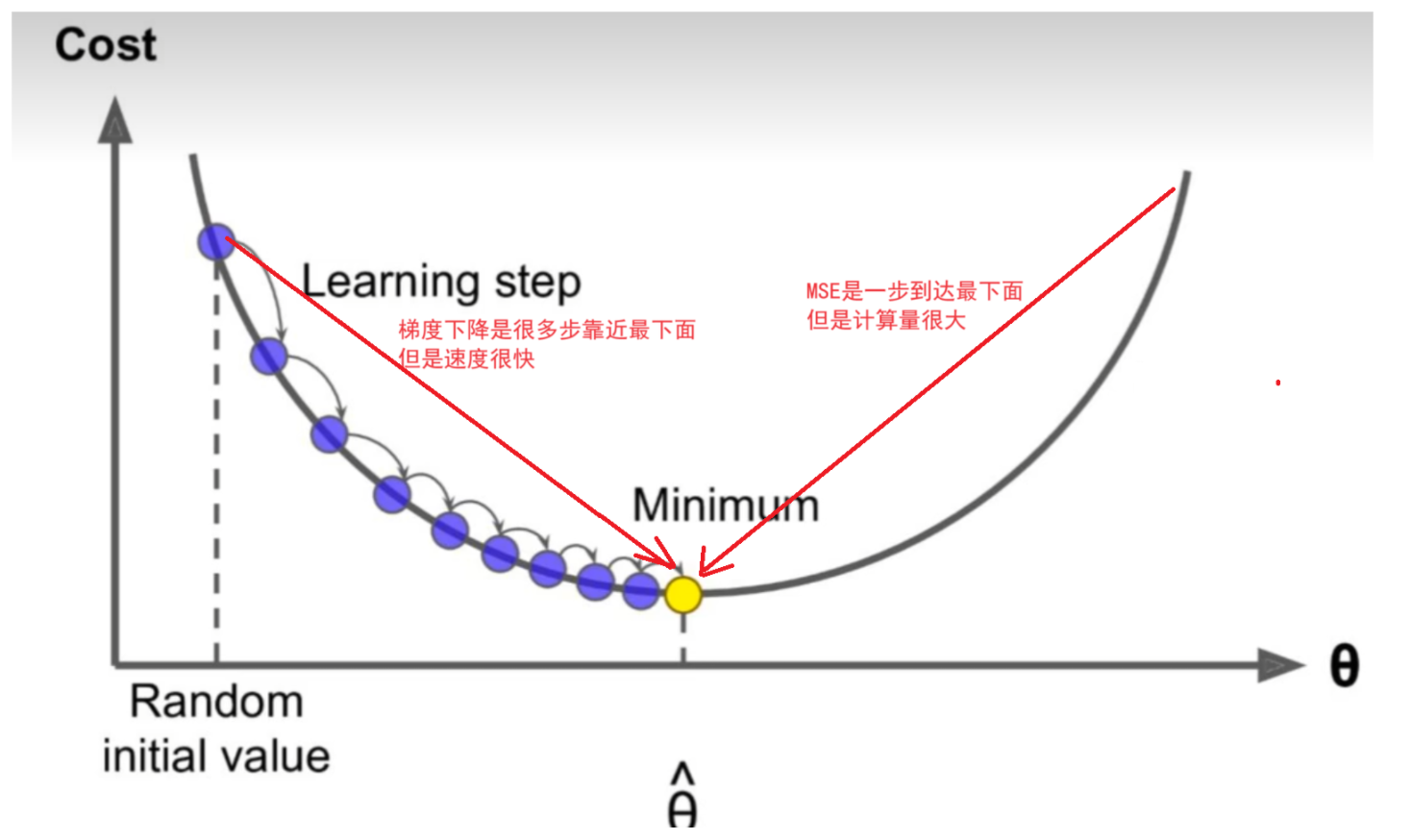
假设你在一个陌生星球的山地上,你想找到一个谷底,那么肯定是想沿着向下的坡行走,如果想尽快的走到谷底,那么肯定是要沿着最陡峭的坡下山。每走一步,都找到这里位置最陡峭的下坡走下一步,这就是梯度下降。
在这个比喻中,梯度就像是山上的坡度,告诉我们在当前位置上地势变化最快的方向。为了尽快走向谷底,我们需要沿着最陡峭的坡向下行走,而梯度下降算法正是这样的方法。
每走一步,我们都找到当前位置最陡峭的下坡方向,然后朝着该方向迈进一小步。这样,我们就在梯度的指引下逐步向着谷底走去,直到到达谷底(局部或全局最优点)。
在机器学习中,梯度表示损失函数对于模型参数的偏导数。具体来说,对于每个可训练参数,梯度告诉我们在当前参数值下,沿着每个参数方向变化时,损失函数的变化率。通过计算损失函数对参数的梯度,梯度下降算法能够根据梯度的信息来调整参数,朝着减少损失的方向更新模型,从而逐步优化模型,使得模型性能更好。
在 $\bar e={\frac{1}{n}}\sum{i=1}^{n}x{i}^{2}w^{2}-{\frac{2}{n}}\sum{i=1}^{n} x{i}y{i}w+{\frac{1}{n}}\sum{i=1}^{n} y_{i}^{2}$ 这个一元二次方程中,损失函数对于参数 w 的梯度就是关于 w 点的切线斜率。梯度下降算法会根据该斜率的信息来调整参数 w,使得损失函数逐步减小,从而找到使得损失最小化的参数值,优化模型的性能。
梯度下降法(Gradient Descent)是一个算法,但不是像多元线性回归那样是一个具体做回归任务的算法,而是一个非常通用的优化算法来帮助一些机器学习算法求解出最优解,所谓的通用就是很多机器学习算法都是用梯度下降,甚至深度学习也是用它来求解最优解。 所有优化算法的目的都是期望以最快的速度把模型参数W求解出来,梯度下降法就是一种经典常用的优化算法。
1.2梯度下降步骤
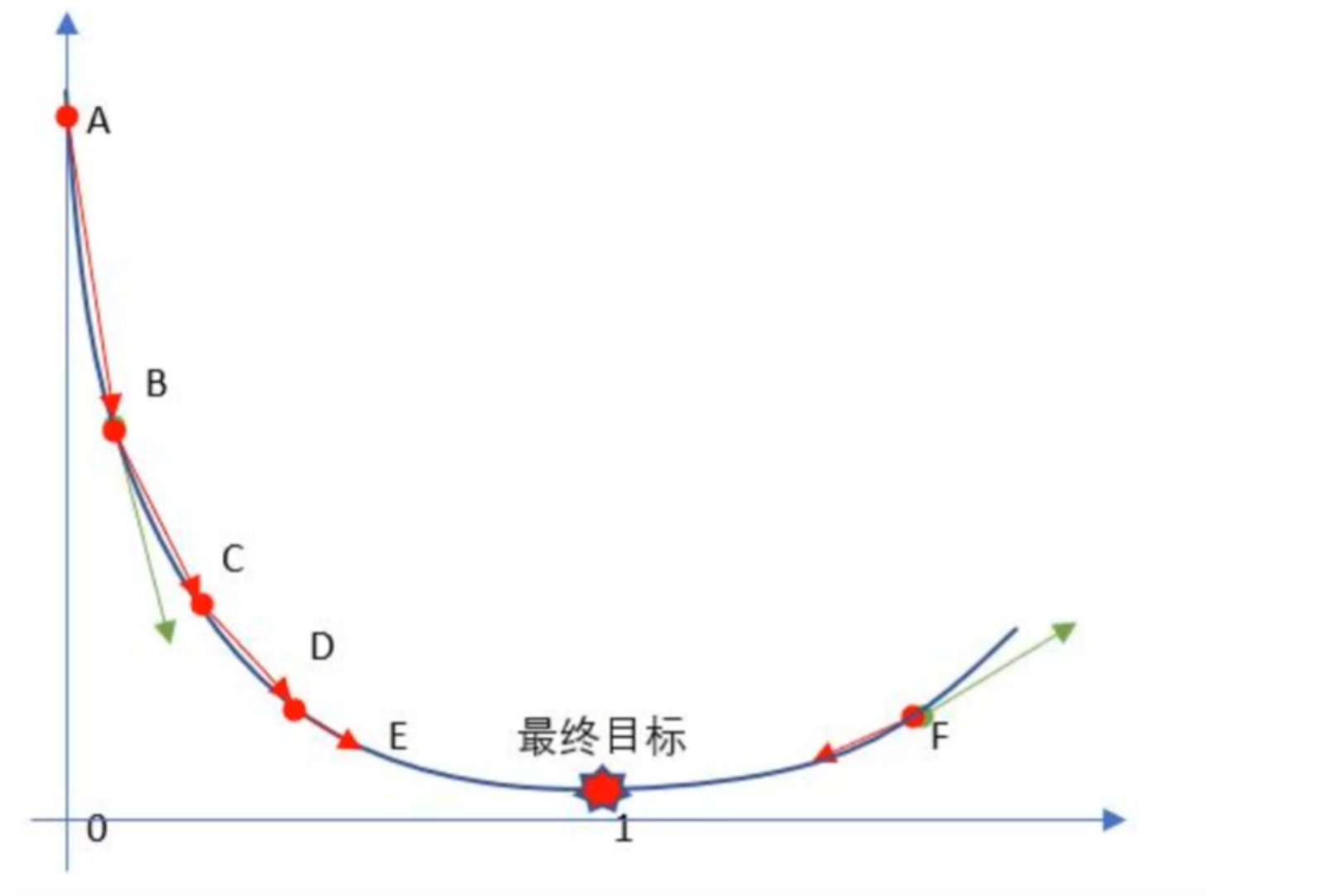
梯度下降流程就是“猜"正确答案的过程:
1、Random随机数生成初始W,随机生成一组成正太分布的数值$w_0,w_1,w_2....w_n$,这个随机是成正太分布的(高斯说的)
2、求梯度g,梯度代表曲线某点上的切线的斜率,沿着切线往下就相当于沿着坡度最陡峭的方向下降.
3、if g < 0,w变大,if g >0,w变小(目标左边是斜率为负右边为正 )
4、判断是否收敛,如果收敛跳出迭代,如果没有达到收敛,回第2步再次执行2~4步收敛的判断标准是:随着迭代进行查看损失函数Loss的值,变化非常微小甚至不再改变,即认为达到收敛
5.上面第4步也可以固定迭代次数
1.3梯度下降公式
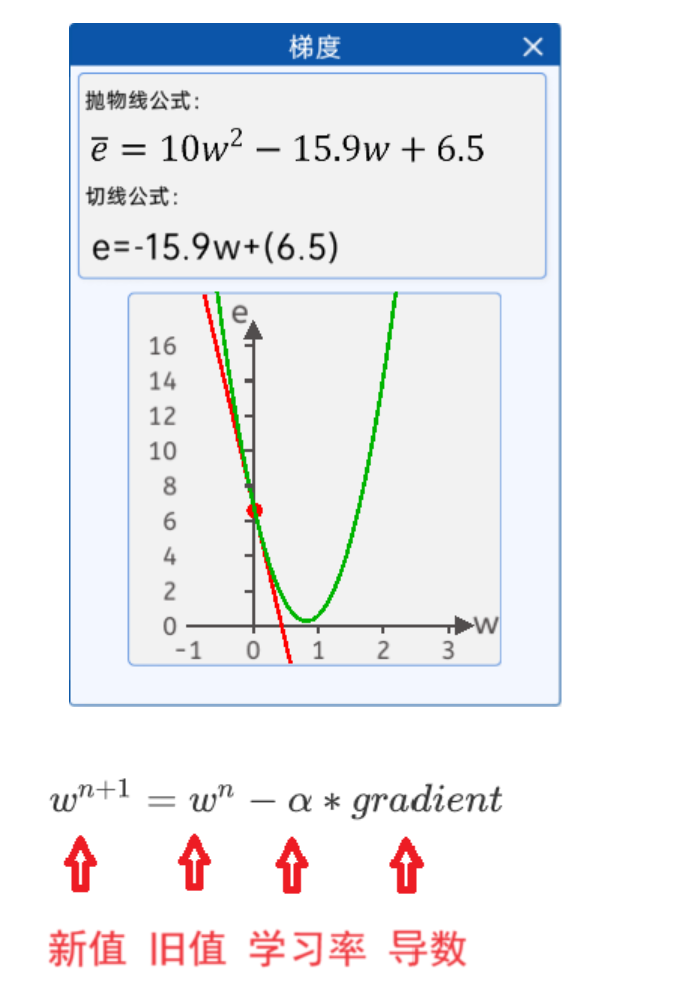
随机给一个w初始值,然后就不停的修改它,直到达到抛物线最下面附近,比如
w=0.2
w=w-0.01*w为0.2时的梯度(导数) 假设算出来是 0.24
w=w-0.01*w为0.24时的梯度(导数) 假设算出来是 0.33
w=w-0.01*w为0.33时的梯度(导数) 假设算出来是 0.51
w=w-0.01*w为0.51时的梯度(导数) 假设算出来是 0.56
w=w-0.01*w为0.56时的梯度(导数) 假设算出来是 0.58
w=w-0.01*w为0.58时的梯度(导数) 假设算出来是 0.62
就这样一直更新下去,会在真实值附近,我们可以控制更新的次数
关于随机的w在左边和右边问题:
因为导数有正负
如果在左边 导数是负数 减去负数就是加 往右移动
如果在右边 导数是正数 减去正数就是减 往左移动
1.4学习率
根据我们上面讲的梯度下降公式,我们知道α是学习率,设置大的学习率α;每次调整的幅度就大,设置小的学习率α;每次调整的幅度就小,然而如果步子迈的太大也会有问题! 学习率大,可能一下子迈过了,到另一边去了(从曲线左半边跳到右半边),继续梯度下降又迈回来,使得来来回回震荡。步子太小呢,就像蜗牛一步步往前挪,也会使得整体迭代次数增加。
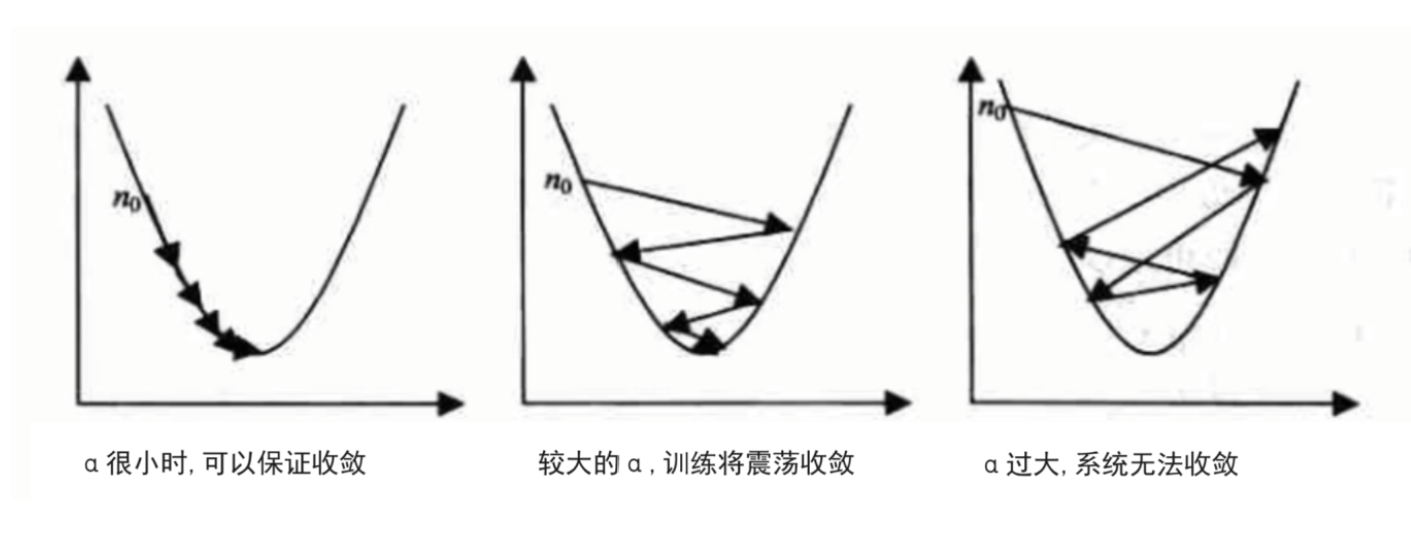
学习率的设置是门一门学问,一般我们会把它设置成一个小数,0.1、0.01、0.001、0.0001,都是常见的设定数值(然后根据情况调整)。一般情况下学习率在整体迭代过程中是不变,但是也可以设置成随着迭代次数增多学习率逐渐变小,因为越靠近山谷我们就可以步子迈小点,可以更精准的走入最低点,同时防止走过。还有一些深度学习的优化算法会自己控制调整学习率这个值
