59. 螺旋矩阵 II|从“左闭右开”的圈层模拟入手(附图解与 C++ 实现)
59. 螺旋矩阵 II|从“左闭右开”的圈层模拟入手(附图解与 C++ 实现)
个人刷题笔记,整理了更清晰的圈层模拟法与统一边界规则,配了过程图,参考与延伸阅读见文末。
题目
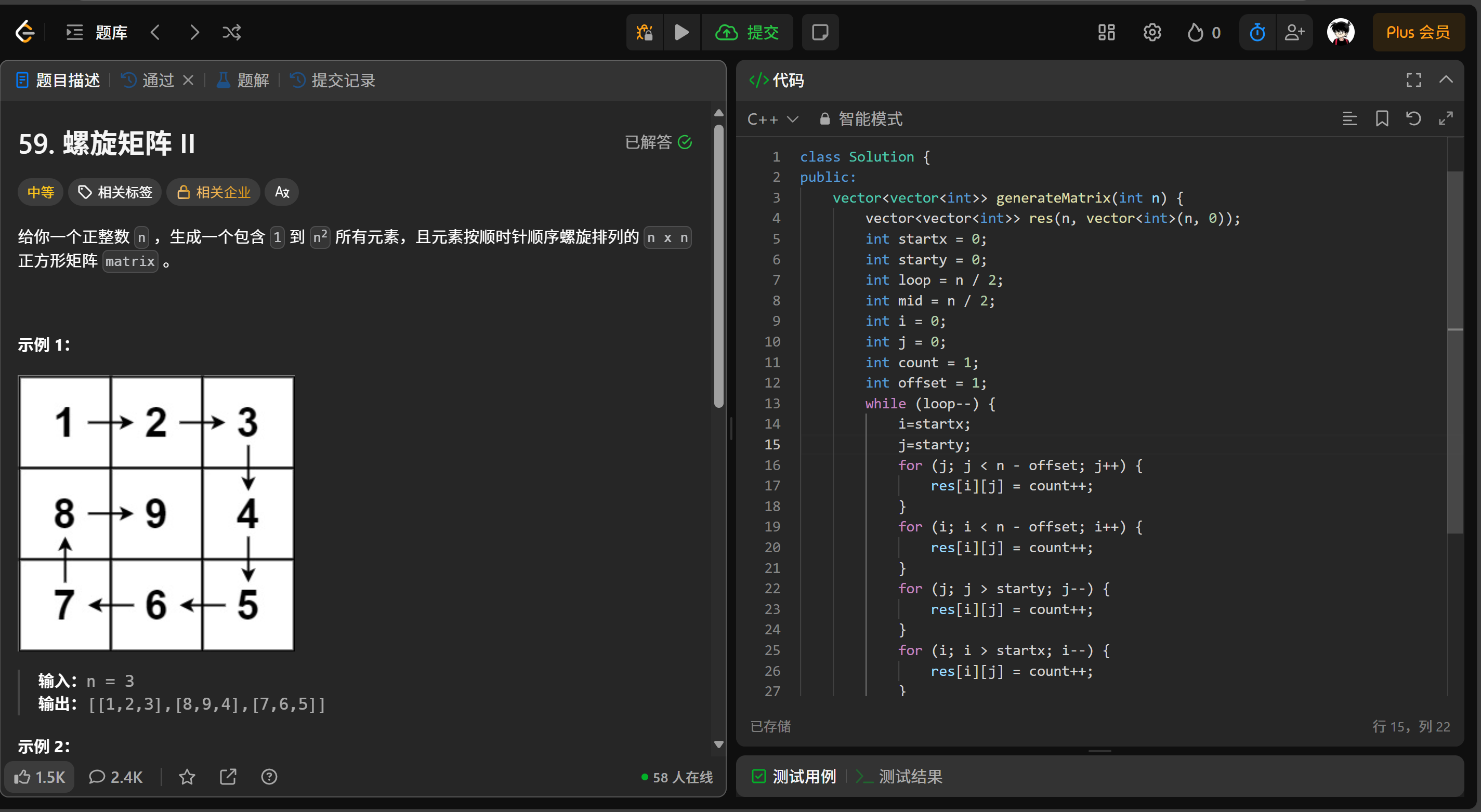
给定正整数 n,生成一个包含 1 到 n^2,按顺时针螺旋排列的 n×n 正方形矩阵。
- 输入:n = 3
- 输出:
[ [1,2,3],[8,9,4],[7,6,5] ]
(核心就两点)
- 圈层推进:从外到内一圈一圈地填数,一圈对应四条边。
- 统一边界规则:每条边都用“左闭右开”,保证拐角处不重复覆盖,代码更整洁不打补丁。
关键变量
- startX/startY:当前圈起点(左上角)
- loop = n / 2:完整圈的数量(奇数时最中心单元格另行处理)
- offset:控制右/下边界缩进量(每圈 +1)
- mid = n / 2:奇数时中心坐标
- count:当前要填的数值,从 1 自增到 n^2
解析
- 圈层定义:第 t 圈覆盖坐标区间 [t, n-1-t] 的四条边(不含已在上一条边写过的拐角)。本实现里 t 由
startX/startY表示,右/下边界由n - offset表示。 - 循环次数:
loop = n / 2。偶数 n 全由圈层完成;奇数 n 还需最后补中心点(mid, mid)。 - 指针语义:
startX, startY:当前圈的左上角。offset:右/下边界的缩进量(每完成一圈自增 1),因此本圈的最右列与最下行下标为n - offset。count:从 1 自增到 n^2 的写入值。
- 循环不变量(进入每一圈前,设
i = startX, j = startY):- 上边:
for (; j < n - offset; ++j)写入(i, startY .. n-offset-1),不包含右上角;结束时j == n - offset。 - 右边:
for (; i < n - offset; ++i)写入(startX .. n-offset-1, j),不包含右下角;结束时i == n - offset。 - 下边:
for (; j > startY; --j)写入(i, n-offset .. startY+1),不包含左下角;结束时j == startY。 - 左边:
for (; i > startX; --i)写入(n-offset .. startX+1, j),不包含左上角;结束时i == startX。至此一圈闭合且没有角点重复写入。
- 上边:
- 统一规则为何用“左闭右开”:四条边都遵循同一开闭区间,使得四个拐角各自只被一次边写入,避免重复与漏写;若混用不同规则,极易出现覆盖或空洞。
- 终止与收缩:完成一圈后执行
startX++,startY++,offset++,圈层向内收缩;当loop次数耗尽即退出。 - 特殊用例:
- n=1:
loop=0,直接补中心(0,0)为 1。 - n=2:只做一圈,得到
[[1,2],[4,3]]。
- n=1:
走一遍 n=3(步骤与坐标)
初始:startX=0, startY=0, offset=1, 右/下边界=2
1) 上边: (0,0)→(0,1) 写入 1,2
2) 右边: (0,2)→(1,2) 写入 3,4
3) 下边: (2,2)→(2,1) 写入 5,6
4) 左边: (2,0)→(1,0) 写入 7,8
中心: (1,1) 写入 9
结果:[[1,2,3],[8,9,4],[7,6,5]]
与“四指针法”的对比
- 经典写法常用
top/bottom/left/right四指针并在每次遍历后判空,逻辑正确但分支较多。 - 本实现用圈层 + 统一“左闭右开”,无需中途判空,结构更规整、边界更容易校验。
排错建议
- 顶边循环应为
j < n - offset,写成<=会覆盖右上角。 - 底边/左边应使用严格大于号
>,否则会覆盖上/右边的拐角。 - 忘记
startX++/startY++/offset++会导致死循环或重复写入。
解题
1)一圈四边的遍历顺序
ASCII 示意(以 n=5,第一圈举例)
(0,0) → → → → (0,3)↓↓↓
(4,3) ← ← ← ← (4,0)
↑
↑
(1,0)
- 说明:每条边都不取最后一个端点,把拐角让给下一条边写入,避免重复。
2)圈层推进与边界收缩
3)奇数中心处理
C++ 实现(可直接提交)
class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> res(n, vector<int>(n, 0));int startX = 0, startY = 0;int loop = n / 2;int mid = n / 2;int offset = 1;int count = 1;while (loop--) {int i = startX, j = startY;// 上:左→右(左闭右开)for (; j < n - offset; ++j) res[i][j] = count++;// 右:上→下(左闭右开)for (; i < n - offset; ++i) res[i][j] = count++;// 下:右→左(左闭右开)for (; j > startY; --j) res[i][j] = count++;// 左:下→上(左闭右开)for (; i > startX; --i) res[i][j] = count++;startX++; startY++; offset++;}if (n % 2 == 1) res[mid][mid] = count;return res;}
};
常见坑位
- 边界风格不统一:一会儿左闭右开、一会儿全闭,极易重复/漏写;统一采用“左闭右开”。
- 圈层收缩遗漏:
startX/startY与offset必须同步推进,否则越界或死循环。 - 奇数中心漏填:循环结束后再单点赋值。
复杂度
- 时间:O(n^2)(每个格子只写一次)
- 空间:O(1) 额外空间(不计返回矩阵)
测试用例
n = 1
n = 2
n = 3
n = 4
n = 5
扩展
- 逆时针:调整四条边的遍历方向顺序即可。
- 从 k 开始填:把
count初始值换成 k。 - 非方阵“圈层遍历”:思路一致,但边界更复杂,通常用上下左右四指针更通用。
参考
- 思路参考:代码随想录《59. 螺旋矩阵 II》一文,链接
