当前位置：首页 > ds >正文

从密度到聚类：DBSCAN算法的第一性原理解析

ds 2025/8/20 9:02:35

从密度到聚类：DBSCAN算法的第一性原理解析

“如果你不能简单地解释它，说明你还没有完全理解它。” —— 理查德·费曼

一、📚引言：为什么需要基于密度的聚类？

想象你在夜空中观察星星。有些星星聚集成星座，有些散落各处，还有些形成了银河。如果让你对这些星星分组，你会怎么做？

🎯 第一性原理思考：聚类的本质是什么？

聚类就是找到数据的自然分组，让组内相似度高，组间相似度低。但"相似"可以有不同的定义：

距离相似：K-means关注的是到中心点的距离
密度相似：DBSCAN关注的是局部密度

传统的K-means算法假设簇是球形的，但现实世界的数据往往不是这样。DBSCAN应运而生，它能发现任意形状的簇。

二、DBSCAN的核心思想：密度定义一切

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) 的核心洞察是：簇是高密度区域，由低密度区域分隔。
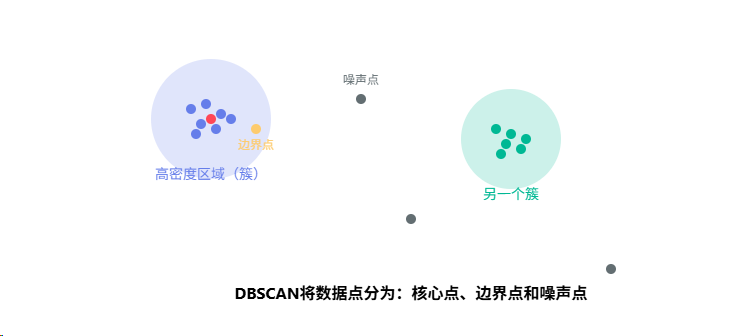
在这里插入图片描述

三、三种样本类型：核心、边界与噪声

🔥 用费曼的方式理解三种点

想象你在一个派对上：

🔴 核心样本（Core Point）：派对中心的活跃分子，周围总是围着很多人（≥min_samples）
🟡 边界样本（Border Point）：站在圈子边缘的人，虽然属于这个圈子，但自己周围人不多
⚫ 噪声样本（Noise Point）：独自站在角落的人，既不在中心，也不属于任何圈子

数学定义

点p是核心点 ⟺ |N_ε§| ≥ min_samples

其中 N_ε§ = {q ∈ D | dist(p,q) ≤ ε}

简单说就是：

以p为中心、半径为ε的圆内，至少有min_samples个点（包括p自己）

四、算法原理：密度可达与密度相连

核心概念解析

直接密度可达：如果点p在点q的ε-邻域内，且q是核心点，则p从q直接密度可达
密度可达：存在一个点的序列p1, p2, …, pn，其中p1=q，pn=p，每个pi+1从pi直接密度可达
密度相连：如果存在点o，使得p和q都从o密度可达，则p和q密度相连

DBSCAN算法流程

def DBSCAN(D, eps, MinPts):"""D: 数据集eps: 邻域半径MinPts: 最小点数(min_samples)"""C = 0  # 簇计数器for P in D:if P.visited:continueP.visited = True# 获取P的ε-邻域NeighborPts = getNeighbors(P, eps)if len(NeighborPts) < MinPts:P.label = NOISE  # 标记为噪声else:C += 1expandCluster(P, NeighborPts, C, eps, MinPts)return clusters

五、代码实现：从理论到实践

1. 训练阶段：发现簇结构

from sklearn.cluster import DBSCAN
import numpy as np# DBSCAN训练：使用预计算的距离矩阵
# 关键参数解释：
# eps: 邻域半径（派对圈子的大小）
# min_samples: 成为核心点的最小邻居数（活跃分子的标准）clustering_model = DBSCAN(eps=0.3,              # 半径阈值min_samples=10,       # 最小样本数metric='precomputed', # 使用预计算的距离矩阵n_jobs=4             # 并行计算
)# 拟合数据
clustering_model.fit(dist_mat)# 获取核心样本索引
core_indices = clustering_model.core_sample_indices_
print(f"发现了 {len(core_indices)} 个核心样本")# 查看簇的分布
unique_labels = set(clustering_model.labels_)
n_clusters = len(unique_labels) - (1 if -1 in unique_labels else 0)
print(f"簇的数量: {n_clusters}")
print(f"噪声点数量: {list(clustering_model.labels_).count(-1)}")

2. 预测阶段：为新样本分配簇标签

在这里插入图片描述

def dbscan_predict_text(model: DBSCAN, pre_datas: List[str], vectorizer: CountVectorizer, x: List[str]) -> np.ndarray:"""DBSCAN预测新样本的簇标签核心思想：1. 提取所有核心样本2. 计算新样本到核心样本的距离3. 如果最小距离 ≤ eps，归属到对应簇4. 否则标记为噪声(-1)参数:model: 训练好的DBSCAN模型pre_datas: 聚类时用到的所有数据vectorizer: 文本向量化器x: 待预测的新样本返回:预测的簇标签数组"""# 获取核心样本（簇的代表）components = [pre_datas[i] for i in model.core_sample_indices_]# 特征转换components_feat = vectorizer.transform(components)x_feat = vectorizer.transform(x)# 计算距离矩阵（使用Jaccard距离）dist_mat = 1 - jaccard_similarity_sparse(x_feat, components_feat).toarray()# 找最近的核心点shortest_dist_idx = dist_mat.argmin(axis=1)  # x对应距离最近的components# 取距离最近的components对应的clustery_new = model.labels_[model.core_sample_indices_[shortest_dist_idx]]# 距离大于eps则置-1（噪声）y_new = np.where(dist_mat.min(axis=1) < model.eps, y_new, -1)return y_new

3. 简化版预测实现

def dbscan_predict_simple(model, X_new, X_train, eps):"""简化版DBSCAN预测"""# 获取核心样本core_indices = model.core_sample_indices_core_samples = X_train[core_indices]# 计算距离distances = compute_distances(X_new, core_samples)# 找最近的核心点min_distances = distances.min(axis=1)nearest_core_idx = distances.argmin(axis=1)# 分配标签y_pred = np.full(len(X_new), -1)  # 默认噪声mask = min_distances <= epsy_pred[mask] = model.labels_[core_indices[nearest_core_idx[mask]]]return y_pred

六、参数调优：min_samples的影响

在这里插入图片描述

参数影响对比

min_samples值	密度门槛	核心点数量	簇的特征	适用场景
较小 (3-5)	低	多	多个小簇，链状结构	发现微小模式
中等 (10-15)	中	适中	平衡的簇大小	一般用途
较大 (20+)	高	少	只保留高密度核心	强噪声过滤

🎯 参数选择经验法则

min_samples ≈ 维度 + 1：这是最小值，保证在d维空间中形成有意义的邻域
min_samples ≈ 2 × 维度：对于高维稀疏数据的推荐值
eps的选择：使用k-距离图，找到"肘点"

# eps参数选择：k-距离图方法
from sklearn.neighbors import NearestNeighborsdef plot_k_distance(X, k):"""绘制k-距离图，帮助选择eps"""nbrs = NearestNeighbors(n_neighbors=k).fit(X)distances, indices = nbrs.kneighbors(X)# 获取第k个最近邻的距离k_distances = distances[:, k-1]k_distances = np.sort(k_distances)# 绘图plt.plot(k_distances)plt.ylabel(f'{k}-NN Distance')plt.xlabel('Data Points sorted by distance')plt.title('K-distance Graph')plt.show()# 使用方法：观察曲线的"肘点"作为eps的参考值
plot_k_distance(X, k=min_samples)

七、高级话题：核心样本的分布分析

统计每个簇的核心样本数

from collections import Counter# 获取核心样本的簇标签
core_labels = model.labels_[model.core_sample_indices_]# 统计分布
core_count = Counter(core_labels)
for cluster_id, count in sorted(core_count.items()):if cluster_id != -1:  # 排除噪声print(f"簇 {cluster_id}: {count} 个核心样本")# 分析簇的密度特征
total_samples_per_cluster = Counter(model.labels_)
for cluster_id in core_count:if cluster_id != -1:density = core_count[cluster_id] / total_samples_per_cluster[cluster_id]print(f"簇 {cluster_id} 的核心密度: {density:.2%}")

💡 关键洞察

核心样本数量反映了簇的"密度质量"：

核心样本占比高 → 簇内部紧密，质量好
核心样本占比低 → 簇较松散，可能包含较多边界点
没有核心样本 → 不可能形成簇（这是DBSCAN的基本原理）

八、DBSCAN vs K-means：本质区别

特征	DBSCAN	K-means
基本假设	簇是高密度区域	簇是球形分布
簇的形状	任意形状	凸形（球形）
簇的数量	自动发现	需要预设
噪声处理	自然识别噪声	强制分配到簇
参数敏感性	对eps和min_samples敏感	对初始中心敏感
计算复杂度	O(n²)最坏情况，O(nlogn)使用索引	O(nkt)，t是迭代次数

九、常见问题与解答

Q1: 每个簇的核心样本数是固定的吗？

不是固定的。min_samples只是判断一个点是否是核心样本的阈值。每个簇里究竟有多少核心样本，取决于该簇的密度分布：

若某簇内部点非常稠密，几乎每个点的邻居都 ≥ min_samples，那么这个簇会有很多核心样本
若另一簇比较"松散"，只有少数几个点周围才够得上min_samples，那它的核心点就比较少

Q2: 如果没有噪声，是不是所有样本都是核心样本？

不一定。没有噪声只说明每个点都能"可达"到某个核心点，但并不意味着它本身就是核心样本。簇的外围那些与核心区连接但邻居 < min_samples的点，虽然被归到该簇（作为边界点），却不是核心样本。

Q3: 边界样本和核心样本的区别是什么？

        核心区域（密集）●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●  ← 核心样本（周围点≥min_samples）●●●●●●●●●●○○○○○      ← 边界样本（在核心点邻域内，但自己不是核心）○○○·        ← 噪声（既不是核心，也不在核心邻域内）

十、实战技巧总结

1. 数据预处理

# 对于文本数据，使用合适的距离度量
from sklearn.feature_extraction.text import TfidfVectorizervectorizer = TfidfVectorizer(max_features=5000)
X = vectorizer.fit_transform(texts)# 计算距离矩阵
from sklearn.metrics.pairwise import cosine_distances
dist_matrix = cosine_distances(X)

2. 参数网格搜索

# 参数优化
from sklearn.metrics import silhouette_scorebest_score = -1
best_params = {}for eps in np.arange(0.1, 1.0, 0.1):for min_samples in range(5, 20, 5):db = DBSCAN(eps=eps, min_samples=min_samples)labels = db.fit_predict(X)# 忽略噪声点计算轮廓系数if len(set(labels)) > 1:score = silhouette_score(X[labels != -1], labels[labels != -1])if score > best_score:best_score = scorebest_params = {'eps': eps, 'min_samples': min_samples}print(f"最佳参数: {best_params}")
print(f"轮廓系数: {best_score}")

3. 可视化结果

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA# 降维可视化
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X.toarray())# 绘制聚类结果
plt.figure(figsize=(10, 8))
unique_labels = set(labels)
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))for k, col in zip(unique_labels, colors):if k == -1:col = 'black'  # 噪声用黑色marker = 'x'else:marker = 'o'class_members = labels == kplt.scatter(X_reduced[class_members, 0], X_reduced[class_members, 1],c=[col], marker=marker, s=50, label=f'Cluster {k}')plt.title('DBSCAN Clustering Results')
plt.legend()
plt.show()