自由学习记录(81)
Compute Shader 代码一共做了两件大事:
-
先用 4 个“基站”算出每只 boid 到基站的距离(相当于给每只 boid 一个 4 维“距离指纹”);
-
再根据 flocking 三法则(分离/对齐/聚合)+ 目标点 + 随机噪声,更新 boid 的方向和位置。
我把两个 kernel 分开讲,再指出几处容易忽略的小坑和可改进点。
ComputeMultilateration(定位/测距)
[numthreads(1,1,1)]
void ComputeMultilateration(uint3 id : SV_DispatchThreadID)
{float3 station_to_position[4] = {float3(500,1000,0), float3(-500,500,-500),float3(0,500,500), float3(0,-500,0)};Boid boid = boidBuffer[id.x];float3 pos = boid.position;float distance_to_station[4] = boid.distance_to_station;// 计算该 boid 到四个固定“基站”的距离,写回它的4维“距离指纹”[unroll] for (int i = 0; i < 4; i++)distance_to_station[i] = distance(pos, station_to_position[i]);boid.distance_to_station = distance_to_station;boidBuffer[id.x] = boid;
}
-
线程布局:
[numthreads(1,1,1)],所以你在 C# 侧用Dispatch(BoidsCount,1,1)是合理的(一个 boid 对应一个线程)。 -
功能:为每个 boid 计算并缓存它到 4 个锚点的距离,后面做“是否邻近”的快速筛选。
理解点:
把“空间中的近邻关系”换成“与相同四个点的距离是否相近”。如果四个距离都差不多,两个 boid 就大概率彼此靠近(多边测距的思想)。
Move(群聚运动)
[numthreads(GROUP_SIZE,1,1)]
void Move(uint3 id : SV_DispatchThreadID)
{uint instanceId = id.x;Boid boid = boidBuffer[instanceId];// 速度扰动:用噪声给每只 boid 略微不同的速度float noise = clamp(noise1(_Time / 100.0 + boid.noise_offset), -1, 1) * 2.0 - 1.0;float velocity = BoidSpeed * (1.0 + noise * BoidSpeedVariation);float3 boid_pos = boid.position;float3 boid_dir = boid.direction;const float boid_distance_to_station[4] = boid.distance_to_station;// 三法则的三个向量项float3 separation = float3(0,0,0);float3 alignment = float3(0,0,0);float3 cohesion = FlockPosition; // 先以目标点为起点参与平均int nearbyCount = 1; // 计数器,从 1 起算(把自身占位考虑入平均)// O(N) 扫一遍其它 boid:先用“距离指纹”粗筛,再用空间距离细筛for (int i = 0; i < BoidsCount; i++) {if (i == instanceId) continue;if (AreBoidsCloseBy(boidBuffer[i].distance_to_station,boid_distance_to_station, NeighbourDistance)){if (distance(boid_pos, boidBuffer[i].position) < NeighbourDistance){float3 otherPos = boidBuffer[i].position;// 分离:越近推力越大(避免重叠)float3 diff = boid_pos - otherPos;float d = length(diff);float k = clamp(1.0 - d / NeighbourDistance, 0.0, 1.0);separation += diff * (k / d);// 对齐:朝邻居平均方向alignment += boidBuffer[i].direction;// 聚合:向邻居位置的平均靠拢cohesion += otherPos;nearbyCount += 1;}}}// 求平均,得到三法则分量float inv = 1.0 / nearbyCount;alignment *= inv;cohesion *= inv;cohesion = normalize(cohesion - boid_pos);// 合成期望方向float3 desired = alignment + separation + cohesion;// 方向平滑过渡(指数平滑)float ip = exp(-RotationSpeed * DeltaTime); // 0..1, dt 越小越接近1boid.direction = lerp((desired), normalize(boid_dir), ip);// 位置更新boid.position += (boid.direction) * (velocity * DeltaTime);boidBuffer[id.x] = boid;
}
逻辑要点:
-
噪声调速:
velocity = BoidSpeed * (1 + noise * variation);让群体看起来自然不齐步。 -
近邻筛选:先比对“到 4 个站的距离差是否都小于阈值”,再做实际空间距离的判断,减少无效计算。
-
三法则:
-
分离 separation:基于距离的反比权(越近推得越开);
-
对齐 alignment:对邻居方向取平均;
-
聚合 cohesion:对邻居位置取平均再指向那个均值。
-
-
方向平滑:用指数衰减
exp(-k*dt)做低通滤波,避免方向瞬变。 -
写回:把更新后的
boid写回boidBuffer。
小坑与建议(强烈建议改/查)
索引越界保护(重要)
Move 用的是 numthreads(GROUP_SIZE,1,1),而 C# 侧用
Dispatch(BoidsCount / GROUP_SIZE + 1, 1, 1)。
最后一组通常是不完整的,所以必须在 kernel 顶部加:
uint i = id.x;
if (i >= BoidsCount) return;
否则最后一组会读写越界。
float d = length(diff);
separation += diff * (k / d);
如果两只 boid 位置重合,d=0 会产出 Inf/NaN。要加 epsilon:
xxxxx
bitonic的效果查看
什么是“双调序列”(Bitonic Sequence)
一个序列如果先单调递增后单调递减(或先递减后递增),就叫双调序列。
例如:
[2, 4, 7, 9, 8, 5, 3] // 先上升(2→9),再下降(9→3)
[9, 7, 4, 3, 5, 8, 10] // 先下降(9→3),再上升(3→10)
循环移位后也算,比如 [9, 8, 5, 3, 2, 4, 7]。
算法核心流程
Bitonic Sort 分两个阶段:
阶段 A:构造双调序列
通过递归或迭代,把原始数据不断分组,每一组先升序排列,另一组降序排列,然后把这两组拼接起来,就得到一个双调序列。
例(长度 8):
原始: [3, 7, 4, 8, 6, 2, 1, 5]
分成两半:
[3, 7, 4, 8] 升序 → [3, 4, 7, 8]
[6, 2, 1, 5] 降序 → [6, 5, 2, 1]
拼接成:
[3, 4, 7, 8, 6, 5, 2, 1] // 双调序列
阶段 B:双调归并(Bitonic Merge)
对于一个双调序列,我们可以并行比较并交换前后对应的元素,使前半段变小,后半段变大,然后递归对两半分别做双调归并,最终得到有序序列。
例(升序目标):
[3, 4, 7, 8, 6, 5, 2, 1]
比较交换 (i, i+4):
[3, 4, 2, 1, 6, 5, 7, 8]
递归处理前半:[3, 4, 2, 1] → 排序
递归处理后半:[6, 5, 7, 8] → 排序
合并完成
特点
-
时间复杂度:O(log² N)
因为每一层归并是 O(log N) 层,每层比较 O(N)。 -
空间复杂度:O(1)(就地交换)
-
并行友好:每一层的比较都可以并行执行,非常适合 GPU / SIMD / FPGA。
-
限制:通常要求 N 为 2 的幂次方(方便分组)。
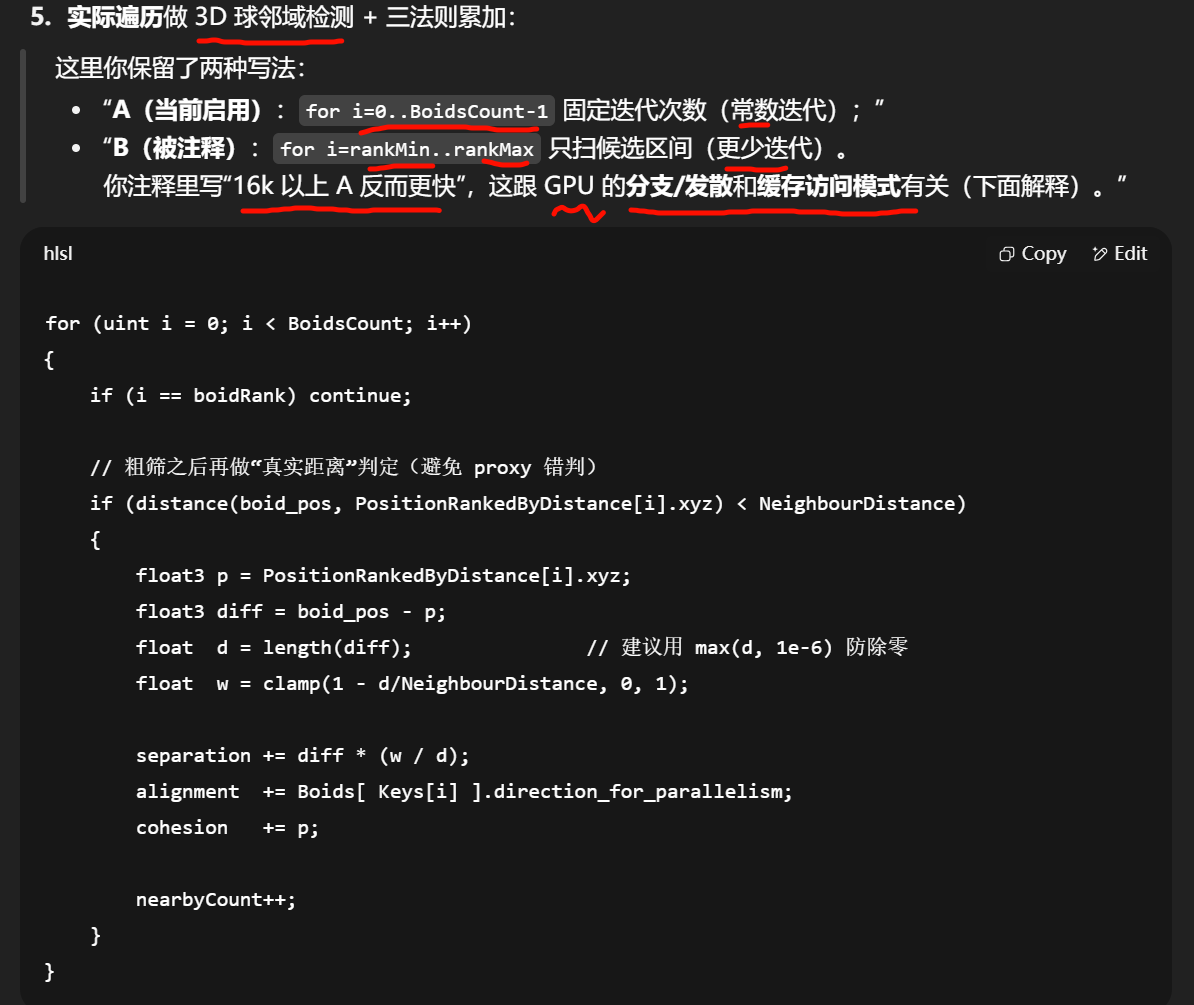
“按标量键排序 + 二分确定 rank 区间 + 真实距离复核”的套路,把 O(N²) 邻居遍历降成了“受控窗口”。你之所以看到“固定总循环有时更快”,是因为 GPU 更怕分支发散与不连续访问——在高 N 时,规则一致的循环 + 连贯内存可能胜过“少算几次但分支乱、缓存差”的写法。
[numthreads(GROUP_SIZE, 1, 1)]
void Move(uint3 id : SV_DispatchThreadID)
{uint instanceId = id.x;Boid boid = Boids[instanceId];float noise = clamp(noise1(_Time / 100.0 + boid.noise_offset), -1, 1) * 2.0 - 1.0;float velocity = BoidSpeed * (1.0 + noise * BoidSpeedVariation);float3 boid_pos = boid.position_for_parallelism;float3 boid_dir = boid.direction_for_parallelism;float boid_distance_to_station = boid.distance_to_station;float3 separation = float3(0.0, 0.0, 0.0);float3 alignment = float3(0.0, 0.0, 0.0);float3 cohesion = FlockPosition;int nearbyCount = 1; // Add self that is ignored in loop//// Binary search on our bitonic sortinguint boidRank = ValueIdxToKeyIdx[instanceId];//获取 Boid 在排序数组中的排名(boidRank)。float minDistanceToBoid = boid_distance_to_station - NeighbourDistance;uint rankMinDistance = getClosestRankForDistance(minDistanceToBoid, 0, boidRank);//二分查找确定距离范围内的 Boid 索引区间(rankMinDistance 到 rankMaxDistance)。float maxDistanceToBoid = boid_distance_to_station + NeighbourDistance;uint rankMaxDistance = getClosestRankForDistance(maxDistanceToBoid, boidRank, BoidsCount - 1);//修正查找算法可能偏差的边界,确保不会漏掉临界点的 Boid。rankMinDistance = max(rankMinDistance - 1, 0); // Fix search algorithm can take one offrankMaxDistance = min(rankMaxDistance + 1, BoidsCount - 1); // Fix search algorithm can take one offuint rankMaxDistancePlusOne = rankMaxDistance + 1;for (uint i = 0; i < BoidsCount; i++){// Faster : Use a constant of iterations each frame seems better than to change it even if it's 10x less...// for (uint i = rankMinDistance; i < rankMaxDistancePlusOne; i++) { // Same behaviour but slower though less iterations...if (i == boidRank)continue;if (distance(boid_pos, PositionRankedByDistance[i].xyz) < NeighbourDistance){float3 tempBoid_position = PositionRankedByDistance[i].xyz;float3 diff = boid_pos - tempBoid_position;float diffLen = (length(diff));float scaler = clamp(1.0 - diffLen / NeighbourDistance, 0.0, 1.0);separation += diff * (scaler / diffLen);alignment += Boids[Keys[i]].direction_for_parallelism; // If I use DirectionRankedByDistance[i] instead it becomes 2x slower...cohesion += tempBoid_position;nearbyCount += 1;}}float avg = 1.0 / nearbyCount;alignment *= avg;cohesion *= avg;cohesion = normalize(cohesion - boid_pos);float3 direction = alignment + separation + cohesion;float ip = exp(-RotationSpeed * DeltaTime);boid.direction = lerp((direction), normalize(boid_dir), ip);boid.position += (boid.direction) * (velocity * DeltaTime);Boids[id.x] = boid;
}-
StructuredBuffer<Boid> Boids;
原始的 Boid 数据(位置、方向、噪声偏移等)。按 instanceId(原始索引) 存放。 -
StructuredBuffer<float4> PositionRankedByDistance;
按某个标量键(你这段里是distance_to_station)排序后的位置表(xyz用,w可当 padding / 备用)。下标 = 排名 boidRank。
-
StructuredBuffer<uint> Keys;
rank → instanceId 的映射(“有序表的第 r 名是哪只 boid”)。
读取其他属性(比如方向)时,需要从Keys[r]反查回原数组Boids[...]。 -
StructuredBuffer<uint> ValueIdxToKeyIdx;
instanceId → rank 的映射(“这只 boid 在有序表里排第几”)。 -
getClosestRankForDistance(dist, lo, hi)
在PositionRankedByDistance对应的“距离键”上做二分,找最接近 dist 的排名(锁定区间端点)。
这些映射是典型的“排序视图”:数据还在原数组里,但再附一套“按某个 key 排序”的 rank 视图,读写互相可跳转。
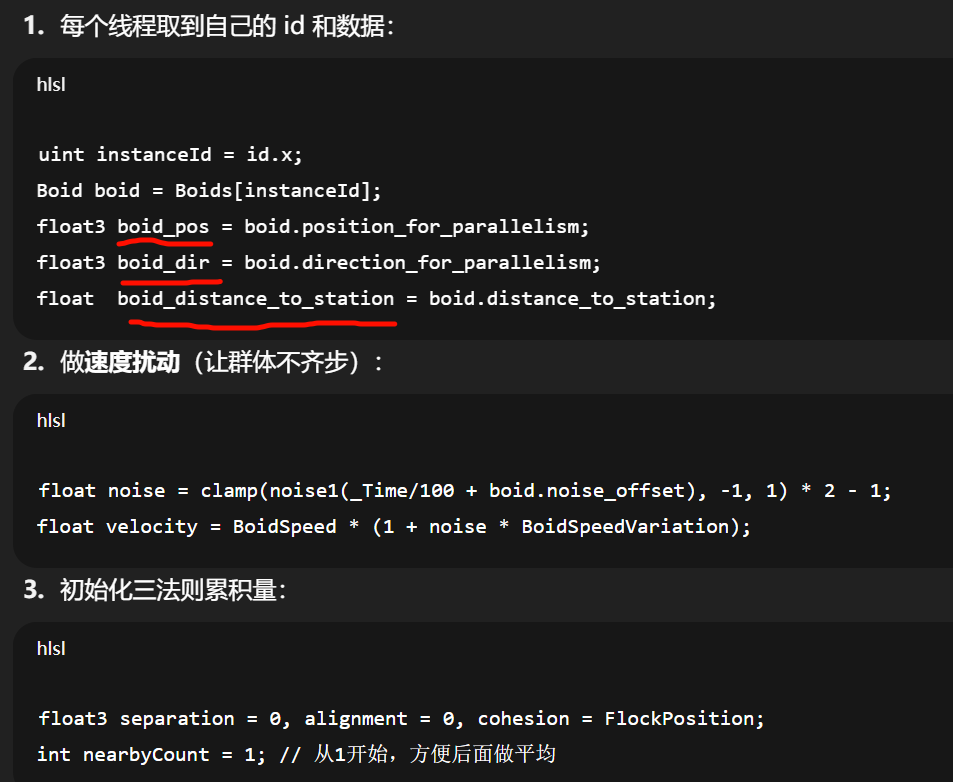
float inv = 1.0 / nearbyCount;
alignment *= inv;
cohesion *= inv;
cohesion = normalize(cohesion - boid_pos);float3 desired = normalize(alignment + separation + cohesion);// 建议的平滑写法(朝 desired 旋转):
float s = 1 - exp(-RotationSpeed * DeltaTime); // 0..1
boid.direction_for_parallelism = normalize(lerp(boid_dir, desired, s));boid.position_for_parallelism += boid.direction_for_parallelism * (velocity * DeltaTime);
为什么“固定迭代更快”有时会发生(>16k 时)
-
GPU 线程束(warp/wavefront)里如果每个线程的循环次数不同(
rankMax - rankMin在每个 boid 上差异大),会产生严重发散:一些线程提前退出、另一些还在跑,硬件得排队执行分支,吞吐掉下去。 -
用 固定迭代次数(
0..BoidsCount-1)虽然算起来更多,但每个线程做完全一样的工作量,发散少,SM/ALU 利用率可能更高。 -
同时,按 rank 顺序访问
PositionRankedByDistance[i]更连贯,缓存命中率也可能更好。
所以你看到的经验:<16k ✚区间迭代更快;>16k 反而固定迭代更快——这正是 GPU 的“少分支/好内存模式 > 少算几次”的典型现象。
建议的小修小补(稳定性 + 性能)
越界保护(和 CPU 侧 Dispatch 配套):
[numthreads(GROUP_SIZE,1,1)] + Dispatch(ceil(BoidsCount/GROUP_SIZE),1,1) 时,最后一组通常不满,建议开头就:
uint instanceId = id.x;
if (instanceId >= BoidsCount) return;
_for_parallelism;结构体的两个属性
不“必须”,但你现在这两对字段(position vs position_for_parallelism、direction vs direction_for_parallelism)其实是在**充当“前一帧快照(只读)+ 本帧写入”**的角色,用来避免并行更新时的“读写相互污染”。是否保留,取决于你怎么组织并行读写。
为什么会想要两份?
在同一个 kernel 里你会:
-
读邻居的“上一状态”来算三法则(需要稳定一致的快照);
-
写自己的“新状态”。
如果只用一份数据,线程 A 改了自己,线程 B 此时读到 A 时就会读到“半新的”数据 → 结果不稳定/帧间抖动。
两份字段等价于对单个 boid 做了场内双缓冲: -
只从
*_for_parallelism读取邻居; -
只写
position/direction自己的新值; -
帧末再把新值拷到
*_for_parallelism,供下一帧读取。
更标准的几种组织方式(供你选)
-
只读
position_for_parallelism/direction_for_parallelism,只写position/direction。 -
每帧末尾跑一个很小的 copy kernel:
Boids[i].position_for_parallelism = Boids[i].position; Boids[i].direction_for_parallelism = Boids[i].direction; -
优点:简单、不用换 buffer;目前你的代码就是这么在用。
-
缺点:每元素多占一份内存(你这个
Boid恰好是 64B,对齐不错,但带宽更大)。
双缓冲 ping-pong(推荐)
-
用两份
RWStructuredBuffer<Boid>:BoidsRead、BoidsWrite。 -
Movekernel 只从Read读,写到Write;帧末 CPU 侧交换指针(或下一帧互换角色)。 -
优点:语义清晰(读的是旧帧,写的是新帧),可把
Boid精简成单份字段(省内存/带宽)。 -
缺点:需要多一份大 buffer(内存换带宽/清晰度)。
在同一个 RWStructuredBuffer 里 读邻居的值,同时写回自己的新值,在一次 Dispatch 的生命周期内没有任何顺序保证。GPU 可能交错执行、乱序写回、缓存合并 —— 你今天“看起来正常”,不代表明天在另一块卡/驱动/编译器优化下还正常。
为什么会“看起来没事”
-
你只写
Boids[instanceId],读Boids[i] (i≠instanceId);很多 GPU 的实际调度会让大多数读取发生在邻居写回之前,所以大部分时候像是在读“上一帧”。 -
更新量小、滤波/插值平滑,会把偶尔的“读到半新值”抹平,所以肉眼不易察觉。
-
但这完全是未定义行为的“偶然对”。换卡、改
GROUP_SIZE、加优化,甚至场景更复杂时,常会出现抖动、发散、NaN。
GPU 内存一致性要点(这就是“别赌运气”的原因)
-
线程/线程组之间无全局顺序保证;同一
Dispatch内,谁先写谁后读不确定。 -
RWStructuredBuffer是 UAV(Unordered Access View)——字面就叫“无序访问”。 -
想在线程间沟通,必须用共享内存 + 局部屏障(
GroupMemoryBarrierWithGroupSync),而你这里是跨线程组的全局数据,无解。 -
内核边界才是全局屏障:
Dispatch结束 → 下一个 kernel 才能“确定地”看到完整写回。
稳妥做法(任选其一)
-
Ping-Pong 双缓冲(推荐)
-
BoidsRead(只读旧帧) →BoidsWrite(只写新帧) -
帧末在 CPU 侧交换引用。读旧写新,彻底没竞态。
-
-
同缓冲体内“双字段”快照(你现在的
*_for_parallelism)-
规则:只从
position_for_parallelism / direction_for_parallelism读;只写position / direction; -
帧末跑一个小 kernel 把新值拷回到
*_for_parallelism。 -
好处:改动少;坏处:占带宽/内存。
-
-
分离 SoA + 必要快照
-
位置、方向各自独立缓冲(甚至
float4对齐),给需要“上一帧”的量做只读快照; -
大规模时访存更规整、带宽更省。
-
无论选哪个,都保证:本帧计算只读旧状态、只写新状态。跨 kernel 的自然屏障负责把“新”变成“旧”。
稳妥做法(任选其一)
-
Ping-Pong 双缓冲(推荐)
-
BoidsRead(只读旧帧) →BoidsWrite(只写新帧) -
帧末在 CPU 侧交换引用。读旧写新,彻底没竞态。
-
-
同缓冲体内“双字段”快照(你现在的
*_for_parallelism)-
规则:只从
position_for_parallelism / direction_for_parallelism读;只写position / direction; -
帧末跑一个小 kernel 把新值拷回到
*_for_parallelism。 -
好处:改动少;坏处:占带宽/内存。
-
-
分离 SoA + 必要快照
-
位置、方向各自独立缓冲(甚至
float4对齐),给需要“上一帧”的量做只读快照; -
大规模时访存更规整、带宽更省。
-
无论选哪个,都保证:本帧计算只读旧状态、只写新状态。跨 kernel 的自然屏障负责把“新”变成“旧”。
你当前管线的小提示
-
你已经把“测距(
ComputeMultilateration)→ Move”分成两个 kernel:这两个 kernel 之间天然有全局屏障,这很好。 -
但在
Move内 仍有“读邻居/写自己”的竞态问题,所以才需要旧状态快照(*_for_parallelism或双缓冲)。 -
另外要记得:
-
if (id.x >= BoidsCount) return;(防越界) -
距离除零:
float d = max(length(diff), 1e-6); -
方向插值建议用
s = 1 - exp(-RotationSpeed*DeltaTime),normalize(lerp(old, desired, s))。
-
专业资料论述
Stack Overflow 上关于 Compute Shader 的 race condition
“First of all, a race condition happens whenever one thread writes to a memory location while another thread reads OR writes from/to that same location. So, yes,
+=is already causing a race condition...”
Game Development Stack Exchange+4Stack Overflow+4gamedev.net+4
这说明:只要你的 shader 线程在运算中修改了某个位置,而别的线程又读(或写)那个位置,就可能出问题。这恰好就是你当前“虽然暂未出现噪乱,但依然在赌运气”的核心问题。
Unity 论坛对双缓冲(ping-pong)的推荐
“ReadWriteBuffers are restricted to only read & write the element at the job index. You can use double buffering strategies to avoid race conditions.”
Unity Discussions
Unity 官方讨论中都建议用“双缓冲”来避免这种竞态:你要么保留两套数据(旧值用于读,写进新值),要么确保在合适的时间点交换。
“键–索引分离”的 Bitonic 排序(双调排序)初始化 + 单轮比较交换(pass)内核。它们把真正要排序的“值”放在 Values,而把“当前顺序”放在 Keys,并维护一个反向映射 ValueIdxToKeyIdx(值下标 → 当前名次)。
InitBitonicSort:初始化“键–值”视图 + 计算排序键
-
为 Bitonic 排序准备三件东西
-
Values[i]:第i个元素的排序键(这里是到站点的距离) -
Keys[i]:当前顺序里第i名对应的原始元素下标 -
ValueIdxToKeyIdx[valueIndex]:原始元素在当前顺序中的名次
-
-
小提醒:你计算了
i = id.x + id.y * MAX_DIM_THREADS,但访问Boids用的是id.x,如果调度用了id.y>0的二维线程格,应把Boids[id.x]改成Boids[i],否则会错读。
BitonicSort:单个 (dim, block) pass 的并行“配对比较 + 交换”
int block; // 当前 pass 的配对跨度(j)
int dim; // 当前子序列大小(k)
uint count; // 元素总数(可≤缓冲大小)[numthreads(GROUP_SIZE, 1, 1)]
void BitonicSort(uint3 id : SV_DispatchThreadID)
{uint i = id.x + id.y * MAX_DIM_THREADS;uint j = i ^ block; // XOR 配对:与距离为 block 的伙伴配对if (j < i || i >= count) return; // 只让 i<j 的线程动手;越界直接返回// rank -> 原始索引uint key_i = Keys[i];uint key_j = Keys[j];// 原始索引 -> 值float value_i = Values[key_i];float value_j = Values[key_j];// (i & dim)==0 → 该半段做“升序”;否则做“降序”float dir = ((i & dim) == 0) ? 1.0 : -1.0;float diff = (value_i - value_j) * dir;if (diff > 0) {// 交换“当前顺序”的两个位置Keys[i] = key_j;Keys[j] = key_i;// 同时更新反向映射:原始元素在新顺序中的名次ValueIdxToKeyIdx[key_i] = j;ValueIdxToKeyIdx[key_j] = i;}
}
-
核心:对每对
(i, j=i^block)做一次比较交换-
block是这一轮的配对跨度(传统伪码里的j) -
dim是当前正在归并的双调段长度(传统伪码里的k)
-
-
方向控制:
(i & dim) == 0的半边做升序,另一半做降序,这是 bitonic-merge 的关键。 -
防竞态:用
if (j < i) return;只让一侧线程负责这对交换,避免两线程同时写同一对元素。 -
为什么只改
Keys/ValueIdxToKeyIdx不改Values:
你按“索引视图”排序——值本身不动,变的是“顺序”。以后要读“名次 r 的值”,就先key=Keys[r]再Values[key];要从原始下标反查名次,用ValueIdxToKeyIdx[valueIndex]。
CPU 侧(或驱动层)怎么驱动多轮 pass
Bitonic Sort 的外层循环要在 C# 里设置 dim 与 block 并多次 Dispatch:
for (uint k = 2; k <= count; k <<= 1) {for (uint j = k >> 1; j > 0; j >>= 1) {// 设置常量 dim=k, block=jcompute.SetInt("dim", (int)k);compute.SetInt("block", (int)j);// 以二维/一维方式分派,使 i = id.x + id.y*MAX_DIM_THREADS 覆盖 0..count-1compute.Dispatch(bitonicKernel, groupsX, groupsY, 1);}
}-
count最好是 2 的幂;不是的话要补齐/填充或在比较时小心处理越界。 -
每次
Dispatch本身就是一个全局内存屏障,因此不同 pass 之间不会读到“半成品”。
Bitonic 这个词不是“二分查找”,它其实指的是一种并行排序网络的形状。
-
二分查找:是在一个排好序的数组里,用一半一半的方式找某个值的位置(查找)。
-
Bitonic 排序:是把一个乱序数组,先组合成一种特殊的“先升后降”或“先降后升”的形状(bitonic sequence),然后不断比较交换,最后变成完全有序(排序)。
什么是 bitonic(双调)?
-
调就是“单调”,意思是一直升或者一直降。
-
双调(bitonic)就是“先升后降”或者“先降后升”的形状。
例子:
-
2, 4, 7, 9, 6, 3 // 先升到 9 再降 -
10, 8, 5, 2, 6, 9 // 先降到 2 再升 -
这种形状有个好处:只要知道它的拐点在哪,你就可以很快地把它完全排好序。
为什么 GPU 爱用 Bitonic Sort?
GPU 适合做那种每个线程做同样的事的算法。
Bitonic 排序是固定的步骤:
-
把数据两两配对比较,交换成“局部有序”。
-
再组合成更大的 bitonic 序列。
-
重复比较交换,直到整个数组有序。
因为比较顺序是固定的(j = i ^ block),
GPU 能提前安排所有线程并行去做比较,不用像普通排序那样东跳西跳。
它和二分查找的区别
-
Bitonic Sort → 是 排序,目标是让所有数据按顺序排好。
-
Binary Search → 是 查找,前提是数据已经有序。
在你代码里:
-
Bitonic Sort:先把 boid 按“到锚点距离”排好序。
-
Binary Search:在排好序的数组里,用距离范围找邻居的 index 区间。
为什么要这样?
如果不用排序,你找邻居只能全遍历 N 次(N² 的复杂度)。
有了排序 + 二分,查找邻居的复杂度能降很多(接近 N log N),大规模 boid 才跑得动。
Bitonic Sort 和你印象中的“一个一个排到位”(比如冒泡排序、插入排序)最大的区别:
它不是按「找一个元素→放到最终位置」的顺序来做的,而是分阶段、固定模式地全局比较交换。
普通排序(冒泡 / 插入)的逻辑
-
你拿一个元素,不停跟前面或后面比较,直到它到正确位置。
-
每一步的比较对象取决于当前的状态(动态的)。
-
顺序是串行的:一个元素位置没定,其他的比较可能等它。
Bitonic Sort 的逻辑
-
不关心某个元素现在是不是在“最终位置”,
先强制把数据分成升序段和降序段(bitonic 段)。 -
然后用一个固定的比较表(谁和谁比)来让所有线程同时去比较交换。
-
经过几轮这样的全局操作,所有元素自然就落到正确顺序。
为什么能做到?
靠的是它的「网络结构」:
-
第 1 阶段:把 2 个元素配成对,比较交换成升序对/降序对。
-
第 2 阶段:把对拼成 4 个元素的段,再比较交换,形成更大的升/降段。
-
第 3 阶段:段拼成更大的段,再比较交换……
-
因为模式是固定的(
j = i ^ block这种按位异或找配对),所以 GPU 每一轮都知道谁跟谁比,不用动态决定。
https://www.youtube.com/watch?v=Z9TA2iz1LME
神奇
快速排序虽然不稳定,但它的排序结果在数值意义上依然是正确的——也就是说,排序完成后数组中元素的值一定是按升序(或降序)排列的。
不稳定只是意味着:
对于值相同的元素,它们在排序后不保证保持原来的先后顺序。
所以:
-
正确性 ✅:按数值顺序排列是没问题的
-
稳定性 ❌:相等值的原顺序可能被打乱
换句话说,如果你只关心排序后的值顺序(比如 [1,1,2,3]),快速排序完全没问题;
但如果相等值背后还带有额外信息(比如学生分数相同但要保留报名顺序),那就要用稳定排序了。

