Graham 算法求二维凸包
前言
本篇文章原为笔者七升八数学论文作业,如有纰漏,请各位指出,在此感激不尽!
二维凸包的定义
我们先看一张图: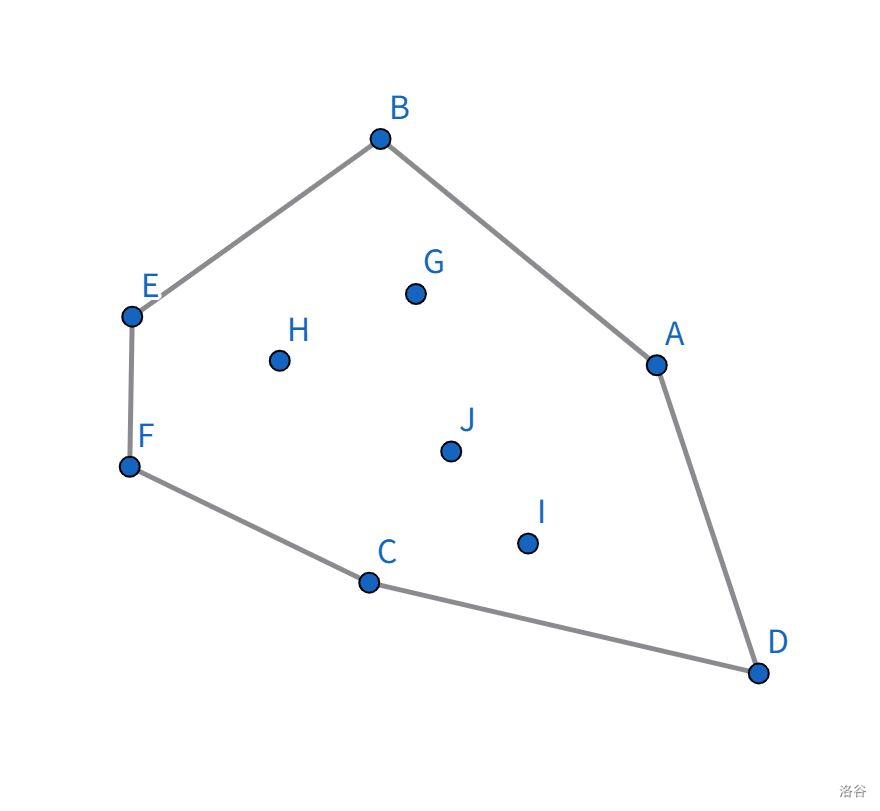
在这张图片里,一个平面上有数个点,同时还有一个凸多边形将这数个点完全覆盖,那么使这个图形面积最小的凸多边形就称为凸包。更具象化地讲,就是用手撑开一个橡皮筋并用其把一堆钉子围住,然后再松开手使橡皮筋收缩,那么最终橡皮筋形成的图形便是这些钉子的凸包。
二维凸包的求法
本文章主要介绍使用 Graham 算法求解二维凸包。
Graham 算法
我们先介绍几个前置知识;
- 极角
- 向量叉积
极角
极角指的是在极坐标中,平面上任意一点到极点的连线与极轴的夹角,如图:
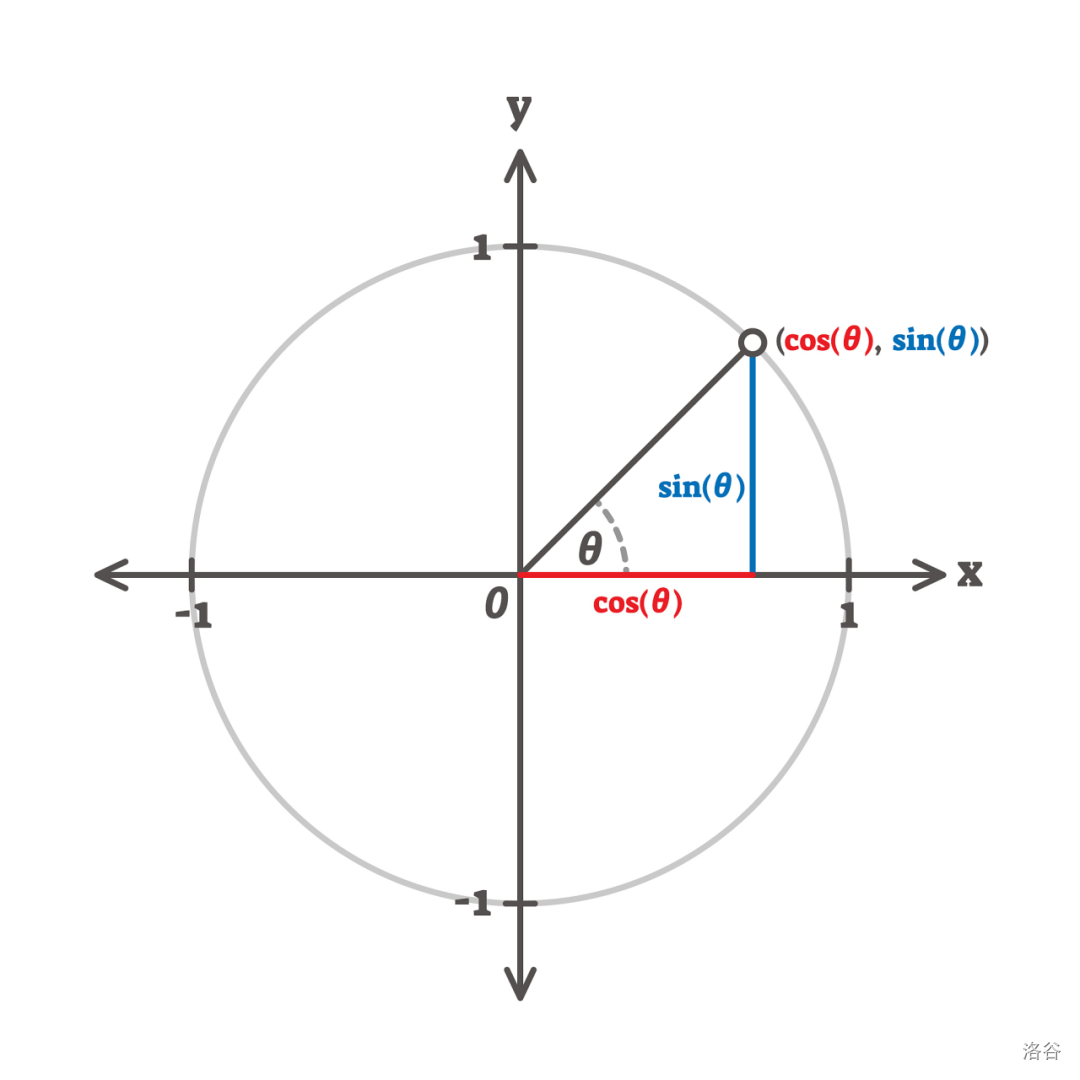
我们设 xxx 为 cos(θ)\cos(\theta)cos(θ),yyy 为 sin(θ)\sin(\theta)sin(θ)。则:
∵tan(yx)=θ\because \tan(\frac{y}x) = \theta∵tan(xy)=θ
∴θ=arctan(yx)\therefore \theta = \arctan(\frac{y}x)∴θ=arctan(xy)
这个公式在进行按极角大小排序时将会很有用。
向量叉积
向量叉乘是有大小有方向,并且不满足交换律的运算。在求解凸包的过程中,我们并不关心向量的大小,而是关心后者,即其方向。由于向量的运算满足右手法则,所以当两向量的叉积为正时,后一个向量便在前者的左边,在下文称之为左拐;否则,若两向量的叉积为负,那么后一个向量便在前者的右边,在下文称之为右拐。如下图:
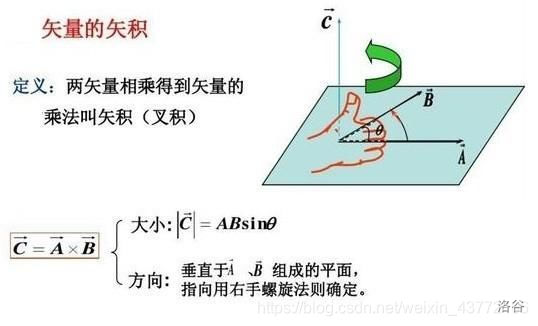
通过该运算,我们可以很清楚的判断两向量的位置关系,这在使用 Graham 算法求解凸包中发挥着很大的作用。
Graham 算法求解凸包
下面我将先介绍一下该算法求解凸包的流程:
- 首先选取一个 yyy 坐标最小的点作为起始节点,如果有多个点的 yyy 坐标相同,那就选择 xxx 坐标做小的点,此点必为凸包上的点。
- 令起始节点为极坐标原点,按平面内其它点的极角从小到大进行排序,如果极角相同,按其到原点的距离从大到小排序。
- 按排序后的顺序将原点和第一个点加入到一个栈中。
- 依次遍历排序后的点,每遍历到一个点时将栈顶的点和栈顶下面的点连线得到直线 lll,然后判断遍历到的新点与栈顶元素所连成的直线与 lll 为左拐、右拐或者处在同一直线上。如果是右拐或在同一直线上,则执行步骤五;否则执行步骤六。
- 栈顶元素不在凸包上,出栈,执行步骤四。
- 新点已处于凸包上,入栈。
- 如果此时排序后的最后一个点以入栈,那么算法结束,否则执行步骤四。
最后,栈中的所有元素便是凸包上的点了。
正确性证明
我们将通过两个方面证明该算法正确性。
栈中所有点均为凸包顶点
- 原点为凸包顶点:因为原点 yyy 坐标以及 xxx 坐标均为最小的,所以它必然为凸包顶点。
- 栈中其它点均为凸包顶点:假设栈中有一点 ppp 不为凸包顶点,那么 ppp 必为凸包边上或内部一点。但因为每次遇到在同一直线上或者在栈顶元素连线的右边的点时都会弹出栈顶元素(即步骤四),这样,便使得凸包内部和边上的点均被弹出。所以凸包边上和内部的点必然不会在算法结束后出现在栈内。
凸包顶点均在栈内
假设凸包顶点 qqq 不在栈内,那么 qqq 必然在算法进行时存在后继点 q1q_1q1 使得 qqq 和 q1q_1q1 所连成的直线与 qqq 和原栈中的元素所连成的直线右拐。但因为在进行极角排序以后,凸包的顶点必然逆时针排列,即凸包的任意连续的三个顶点 pi−1,pi,pi+1p_{i-1}, p_i, p_{i+1}pi−1,pi,pi+1 均满足左拐。所以在处理凸包顶点 qqq 与后继节点 q1q_1q1 时必满足左拐,所以 qqq 必然在栈内。
时间复杂度分析
在算法过程中极角排序的时间复杂度为 O(nlogn)O(n\log n)O(nlogn),而每个点只会入栈和出栈一次,所以时间复杂度为 O(n)O(n)O(n)。总时间复杂度为 O(nlogn)O(n\log n)O(nlogn),效率较高。
代码实现(实现语言为 C++)
对于极角排序,我们可以使用内置的 atan2函数,即计算 arctan\arctanarctan 值。而每次判断栈顶元素是否需要出栈便相当于判断此时栈顶的两个点 AAA,BBB 和 新点 CCC 是否满足 AB→\overrightarrow{AB}AB 与 BC→\overrightarrow{BC}BC 是否为左拐,这便是判断 AB→×BC→≥0\overrightarrow{AB} \times \overrightarrow{BC} \ge 0AB×BC≥0,我们可以使用向量叉积来判断。
以下 C++ 求解凸包的代码:
#include<bits/stdc++.h>
#define ll long long
#define inf (1ll << 62)
#define pb push_back
#define mp make_pair
#define PII pair<int , int>
#define fi first
#define se second
using namespace std;
struct Point {long double x , y , a;
};
vector<Point>pos;inline long double dis(Point a , Point b) {//计算两点距离return sqrtl((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}inline long double cross(Point a , Point b) {//计算向量叉积return a.x * b.y - b.x * a.y;
}inline void solve() {int n;cin >> n;for(int i = 0;i < n;i ++) {long double x , y;cin >> x >> y;pos.pb({x , y , 0});}for(int i = 1;i < n;i ++) {//找出 y 坐标且 x 坐标最小的点if(pos[i].y < pos[0].y || (pos[i].y == pos[0].y && pos[i].x < pos[0].x)) {swap(pos[i] , pos[0]);} }for(int i = 1;i < n;i ++) {//计算极角pos[i].a = atan2(pos[i].y - pos[0].y , pos[i].x - pos[0].x);}sort(pos.begin() + 1 , pos.end() , [](Point &x , Point &y) {//极角排序if(x.a == y.a) return dis(pos[0] , x) > dis(pos[0] , y);return x.a < y.a;});vector<int>st(n + 1);int top = 0;st[++ top] = 0;st[++ top] = 1;for(int i = 2;i < n;i ++) {//维护栈while(top >= 2 && cross({pos[st[top]].x - pos[st[top - 1]].x , pos[st[top]].y - pos[st[top - 1]].y} , {pos[i].x - pos[st[top]].x , pos[i].y - pos[st[top]].y}) < 0) top --;st[++ top] = i;}long double ans = 0;int last = 0;for(int i = top;i >= 1;i --) {//计算凸包周长ans += dis(pos[st[i]] , pos[last]);last = st[i];}cout << fixed << setprecision(2) << ans << "\n";return;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t --) {solve();}return 0;
}
