当前位置：首页 > backend >正文

【机器学习】支持向量机（SVM）

backend 2025/5/22 5:52:56

一、支持向量机基本概念

1.1 定义

1.2 支持向量：距离超平面最近的样本点，决定了超平面的位置。

二、线性支持向量机

2.1 硬间隔支持向量机

2.2 软间隔支持向量机

三、非线性支持向量机

3.1 核函数

3.2 常用核函数

3.2.1 线性核：等价于线性SVM，适合线性可分数据。

3.2.2 多项式核：适合数据具有多项式关系，参数c>=0控制常数项，d控制多项式阶数

3.2.3 高斯核（RBF核）：适合复杂非线性数据，参数控制映射的局部性。

3.2.4 Sigmoid核：类似神经网络激活函数，参数,c控制形状

四、实战：SVM垃圾邮件分类器实现

4.1 项目分析

4.2 代码实现

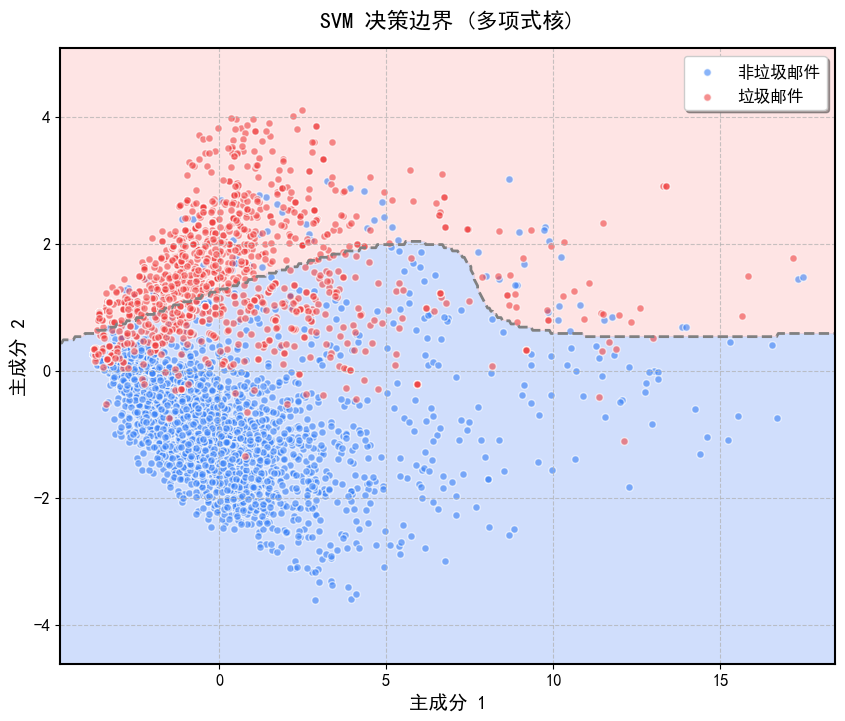
4.3 结果显示（可视化）

一、支持向量机基本概念

1.1 定义

SVM是一种基于统计学习理论的监督学习模型，旨在找到一个最优超平面，将不同类别的数据点分隔开，同时最大化分类间隔（Margin）

具体来说：

在线性可分时，在原空间寻找两类样本的最优分类超平面。
在线性不可分时，加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分，这样就可以在该特征空间中寻找最优分类超平面。

1.2 支持向量：距离超平面最近的样本点，决定了超平面的位置。

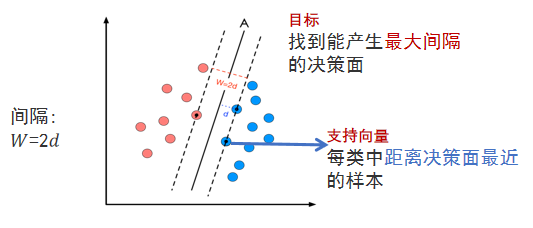
二、线性支持向量机

线性支持向量机假设数据是线性可分的，目标是找到一个超平面 $w^{T}x+b=0$ ，将不同类别的数据点分隔开，并最大化分类间隔。

2.1 硬间隔支持向量机

适用场景：数据完全线性可分，无噪声干扰。

目标：找到一个超平面，使得所有数据点被正确分类，且到最近数据点（支持向量）的间隔最大。

（1）超平面： $w^{T}+b=0$

（2）间隔：数据点 $x_{i}$ 到超平面的距离为 $\frac{|w^T x_i + b|}{||w||}$ 。

支持向量是距离超平面最近的点，满足： $w^T x_i + b = \pm 1$

（3）最大化间隔等价于使 $\frac{1}{||w||}$ 最大，即最小化 $||w||^{2}$

优化目标：最小化法向量范数的平方 $\min_{w, b} \frac{1}{2} \|w\|^2$

约束条件：确保所有数据点被正确分类且位于间隔边界之外 $y_i (w^T x_i + b) \geq 1, \quad \forall i$

其中 $x_{i}$ 是数据点， $y_i \in \{ +1, -1 \}$ 是类别标签，w是法向量，b是偏置

拉格朗日对偶问题：

引入拉格朗日乘子𝛼𝑖≥0，构造拉格朗日函数：

$L(w, b, \alpha) = \frac{1}{2} \|w\|^2 - \sum_i \alpha_i [y_i (w^T x_i + b) - 1]$

对w和b求偏导并令其为0：

$\frac{\partial L}{\partial w} = w - \sum_i \alpha_i y_i x_i = 0 \implies w = \sum_i \alpha_i y_i x_i$

$\frac{\partial L}{\partial b} = -\sum_i \alpha_i y_i = 0 \implies \sum_i \alpha_i y_i = 0$

代回拉格朗日函数，得到对偶问题： $\max_{\alpha} \sum_i \alpha_i - \frac{1}{2} \sum_i \sum_j \alpha_i \alpha_j y_i y_j (x_i^T x_j)$
约束条件： $\sum_i \alpha_i y_i = 0, \quad \alpha_i \geq 0$

求解方法：使用序列最小优化（SMO）算法等方法求解 $\alpha_i$ ，然后计算w和b。

预测：对于新数据点x，分类决策函数为： $f(x) = \text{sign} \left( \sum_i \alpha_i y_i (x_i^T x) + b \right)$

2.2 软间隔支持向量机

适用场景：数据近似线性可分，存在噪声或少量误分类点。

核心思想：引入松弛变量 $\xi_i \geq 0$ ,允许部分数据点位于间隔内或被误分类，通过惩罚参数C平衡间隔最大化与误分类最小化。

优化目标：最小化法向量范数的同时，控制误分类的惩罚 $\min_{w, b, \xi} \frac{1}{2} \|w\|^2 + C \sum_i \xi_i$

约束条件：允许数据点偏离正确分类的间隔 $y_i (w^T x_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0, \quad \forall i$

其中，C>0是惩罚参数， $\xi_i \geq 0$ 是松弛变量，表示数据点偏离正确分类的程度

几何意义：

𝜉𝑖=0：数据点正确分类且在间隔外。

0<ξi≤1：数据点在间隔内但分类正确。

ξi>1：数据点被误分类。

C 控制间隔大小与误分类的权衡：C 越大，惩罚误分类越多，模型更严格；C 越小，允许更多误分类，间隔更大。

拉格朗日对偶问题：

构造拉格朗日函数：

$L(w, b, \xi, \alpha, \mu) = \frac{1}{2} \|w\|^2 + C \sum_i \xi_i - \sum_i \alpha_i [y_i (w^T x_i + b) - 1 + \xi_i] - \sum_i \mu_i \xi_i$

对w，b， $\xi$ 求偏导并令其为0： $w = \sum_i \alpha_i y_i x_i, \quad \sum_i \alpha_i y_i = 0, \quad \alpha_i + \mu_i = C$
代回得到对偶问题： $\max_{\alpha} \sum_i \alpha_i - \frac{1}{2} \sum_i \sum_j \alpha_i \alpha_j y_i y_j (x_i^T x_j)$
约束条件： $\sum_i \alpha_i y_i = 0, \quad 0 \leq \alpha_i \leq C$

求解方法：使用序列最小优化（SMO）算法等方法求解 $\alpha_i$ ，然后计算w和b。

预测：对于新数据点x，分类决策函数为： $f(x) = \text{sign} \left( \sum_i \alpha_i y_i (x_i^T x) + b \right)$

三、非线性支持向量机

当数据线性不可分时（例如，数据点在二维空间呈环形或交叉分布），通过核函数将数据映射到高维空间，使其在高维空间中线性可分。

3.1 核函数

核心思想：

显式映射到高维空间计算复杂，核函数通过计算低维空间的内积 𝐾(𝑥𝑖,𝑥𝑗)=𝜙(𝑥𝑖)𝑇𝜙(𝑥𝑗)替代高维计算。
核函数满足Mercer条件（正定性），确保对偶问题的凸性。

数学表述：

对偶问题与软间隔SVM一致，但用核函数替换内积 $\max_{\alpha} \sum_i \alpha_i - \frac{1}{2} \sum_i \sum_j \alpha_i \alpha_j y_i y_j K(x_i, x_j)$

约束条件： $\sum_i \alpha_i y_i = 0, \quad 0 \leq \alpha_i \leq C$

决策函数： $f(x) = \text{sign} \left( \sum_i \alpha_i y_i K(x_i, x) + b \right)$

3.2 常用核函数

3.2.1 线性核：等价于线性SVM，适合线性可分数据。

$K(x_i, x_j) = x_i^T x_j$

3.2.2 多项式核：适合数据具有多项式关系，参数c>=0控制常数项，d控制多项式阶数

$K(x_i, x_j) = (x_i^T x_j + c)^d$

3.2.3 高斯核（RBF核）：适合复杂非线性数据，参数 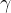$\gamma$ 控制映射的局部性。

$K(x_i, x_j) = \exp(-\gamma \|x_i - x_j\|^2)$

$\gamma$ 越大，模型越倾向于拟合局部数据（可能过拟合）；
$\gamma$ 越小，模型更平滑。

3.2.4 Sigmoid核：类似神经网络激活函数，参数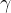 $\gamma$ ,c控制形状

$K(x_i, x_j) = \tanh(\gamma x_i^T x_j + c)$

四、实战：SVM垃圾邮件分类器实现

4.1 项目分析

任务：构建一个垃圾邮件分类器，用于区分垃圾邮件（y=1）和非垃圾邮件（y=0）。

方法：使用支持向量机（SVM）分类器，尝试不同的核函数（线性核、多项式核、RBF核）。

数据：

vocab.txt：词汇表，包含1899个单词及其索引。
emailSample1.txt：示例邮件，用于测试特征提取。
spamTrain.mat 和 spamTest.mat：预处理后的训练和测试数据集，包含1899维二值特征向量和标签。

可视化：通过PCA降维到2D，绘制SVM的决策边界，展示不同核函数的分类效果。

4.2 代码实现

import numpy as np
import scipy.io
import re
import os
from sklearn.svm import SVC
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import matplotlib# 设置 Matplotlib 支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False# 步骤 1：加载词汇表
def load_vocabulary(vocab_file):"""从 vocab.txt 加载词汇表（单词到索引的映射）。"""if not os.path.exists(vocab_file):raise FileNotFoundError(f"文件 {vocab_file} 不存在，请检查路径或文件是否正确。")vocab = {}with open(vocab_file, 'r', encoding='utf-8') as f:for line in f:index, word = line.strip().split()vocab[word] = int(index)return vocab# 步骤 2：将邮件转换为特征向量
def process_email(email_content, vocab):"""将邮件文本转换为 1899 维二值特征向量。"""feature_vector = np.zeros(len(vocab))email_content = email_content.lower()email_content = re.sub(r'[^\w\s]', '', email_content)words = email_content.split()for word in words:if word in vocab:feature_vector[vocab[word] - 1] = 1return feature_vector# 步骤 3：加载训练和测试数据
def load_mat_data(train_file, test_file):"""加载 spamTrain.mat 和 spamTest.mat。"""if not os.path.exists(train_file):raise FileNotFoundError(f"文件 {train_file} 不存在，请检查路径。")if not os.path.exists(test_file):raise FileNotFoundError(f"文件 {test_file} 不存在，请检查路径。")train_data = scipy.io.loadmat(train_file)test_data = scipy.io.loadmat(test_file)X_train = train_data.get('X', train_data.get('Xtest'))y_train = train_data.get('y', train_data.get('ytest')).ravel()X_test = test_data.get('X', test_data.get('Xtest'))y_test = test_data.get('y', test_data.get('ytest')).ravel()return X_train, y_train, X_test, y_test# 步骤 4：训练和评估 SVM
def train_svm(X_train, y_train, X_test, y_test, kernel='linear', **kwargs):"""训练 SVM 分类器并评估准确率。"""clf = SVC(kernel=kernel, **kwargs)clf.fit(X_train, y_train)train_accuracy = clf.score(X_train, y_train)test_accuracy = clf.score(X_test, y_test)return clf, train_accuracy, test_accuracy# 步骤 5：可视化 2D 决策边界（美化版）
def plot_decision_boundary(X, y, clf, kernel_name):"""使用 PCA 降维到 2D 并绘制美化的决策边界。"""# PCA 降维到 2Dpca = PCA(n_components=2)X_2d = pca.fit_transform(X)# 训练 2D 分类器params = clf.get_params()clf_2d = SVC(**params)clf_2d.fit(X_2d, y)# 创建网格h = 0.05  # 增大步长，减少计算量并平滑边界x_min, x_max = X_2d[:, 0].min() - 1, X_2d[:, 0].max() + 1y_min, y_max = X_2d[:, 1].min() - 1, X_2d[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# 预测网格点类别Z = clf_2d.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# 创建画布并设置大小plt.figure(figsize=(10, 8), dpi=100)# 绘制决策边界（使用更柔和的配色）plt.contourf(xx, yy, Z, levels=[-1, 0, 1], colors=['#A3BFFA', '#FECACA'], alpha=0.5)plt.contour(xx, yy, Z, levels=[0], colors='gray', linestyles='--', linewidths=2)# 绘制数据点（分别绘制两类，添加标签用于图注）spam = y == 1non_spam = y == 0plt.scatter(X_2d[non_spam, 0], X_2d[non_spam, 1], c='#3B82F6', s=30, alpha=0.6, edgecolors='white',label='非垃圾邮件')plt.scatter(X_2d[spam, 0], X_2d[spam, 1], c='#EF4444', s=30, alpha=0.6, edgecolors='white', label='垃圾邮件')# 设置标题和标签（增大字体，调整样式）plt.title(f'SVM 决策边界 ({kernel_name})', fontsize=16, pad=15)plt.xlabel('主成分 1', fontsize=14)plt.ylabel('主成分 2', fontsize=14)# 添加图注plt.legend(loc='upper right', fontsize=12, frameon=True, shadow=True)# 添加网格线plt.grid(True, linestyle='--', alpha=0.7)# 调整刻度字体plt.tick_params(axis='both', which='major', labelsize=12)# 设置边框样式ax = plt.gca()ax.spines['top'].set_linewidth(1.5)ax.spines['right'].set_linewidth(1.5)ax.spines['left'].set_linewidth(1.5)ax.spines['bottom'].set_linewidth(1.5)# 保存图像plt.savefig(f'decision_boundary_{kernel_name.lower()}.png', bbox_inches='tight')plt.close()# 主函数
def main():# 文件路径vocab_file = 'D:/Desktop/Code/ML/ML/SVM/svm_data/data/vocab.txt'train_file = 'D:/Desktop/Code/ML/ML/SVM/svm_data/data/spamTrain.mat'test_file = 'D:/Desktop/Code/ML/ML/SVM/svm_data/data/spamTest.mat'email_file = 'D:/Desktop/Code/ML/ML/SVM/svm_data/data/emailSample1.txt'# 检查文件是否存在for file in [vocab_file, email_file, train_file, test_file]:if not os.path.exists(file):print(f"错误：文件 {file} 不存在，请检查路径。")return# 加载词汇表vocab = load_vocabulary(vocab_file)print(f"词汇表大小: {len(vocab)}")# 处理示例邮件with open(email_file, 'r', encoding='utf-8') as f:email_content = f.read()sample_features = process_email(email_content, vocab)print(f"示例邮件特征向量维度: {sample_features.shape}")# 加载训练和测试数据X_train, y_train, X_test, y_test = load_mat_data(train_file, test_file)print(f"训练数据维度: {X_train.shape}, 测试数据维度: {X_test.shape}")# 定义核函数和参数kernels = [('线性核', {'kernel': 'linear', 'C': 1.0}),('多项式核', {'kernel': 'poly', 'degree': 3, 'C': 1.0}),('RBF核', {'kernel': 'rbf', 'gamma': 'scale', 'C': 1.0})]# 训练并评估 SVMfor kernel_name, params in kernels:print(f"\n正在训练 {kernel_name} 的 SVM 模型...")clf, train_acc, test_acc = train_svm(X_train, y_train, X_test, y_test, **params)print(f"{kernel_name} - 训练集准确率: {train_acc:.4f}, 测试集准确率: {test_acc:.4f}")plot_decision_boundary(X_train, y_train, clf, kernel_name)print(f"决策边界图已保存为 'decision_boundary_{kernel_name.lower()}.png'")if __name__ == "__main__":main()