计算机图形学基础--Games101笔记（一）数学基础与光栅化

数学基础

向量

点乘，叉乘和投影：

插值

三角形插值

**重心坐标：**我们通过任意点的重心坐标来插值。$V=\alpha V_A+\beta V_B+\gamma V_C$。注意重心坐标没有投影不变性，如果插值三维属性，需要利用投影前的坐标插值。例如深度插值应该用三维空间坐标。

双线性插值

平面定义

法线-点表示

第一部分：光栅化

坐标变换

二维变换

从上述公式中我们发现，平移变换需要两个向量的加和，为了使得所有的变换统一写成矩阵乘法的形式，我们引入齐次坐标。在齐次坐标中，每个点表示为：$(x,y,1{)}^{\mathrm{T}}$,每个向量表示为：$(x,y,0{)}^{\mathrm{T}}$。通过这种方式我们可以确保，点加点等于点（中点），点减点等于向量，向量加减向量还是向量。点加减向量还是向量。特别地，我们认为$(x,y,k{)}^{\mathrm{T}}=(x/k,y/k,1{)}^{\mathrm{T}}$。在引入齐次坐标后，平移可以写成：

在其次坐标系下的变化矩阵最后一行一般都是001，左上角是缩放，拉伸，镜像，旋转变化，最后一列是平移变换。在这种情况下，是先进性二维变换，在进行平移变换。

如果要求逆变换，求矩阵的逆即可。由于矩阵乘积不满足交换律，因此计算的时候不可更改变换矩阵的顺序。注意旋转矩阵是正交矩阵，求旋转矩阵的逆相当于求旋转矩阵的转置。

3D变换

在三位空间中点和向量的描述形式和二维空间类似（只增加了一个z维）。三位空间中的旋转和二位空间有些许不同。我们按照xyz的顺序构建坐标系，沿x轴旋转的时候yxz是x轴，沿y轴旋转的时候xz是-y轴。因此需要添加符号（conx=-conx）

我们可以通过分解的方式，吧沿任意轴旋转a度分解为沿xyz轴分别旋转a1,b1,c1度。也可以通过三位旋转矩阵直接求沿着任意轴旋转。$R(n,\alpha )$是沿着空间中任意一个轴n逆时针旋转$\alpha$度后的结果。

视图变换（MVP）

投影变换

投影变换分为两种：正交投影和透视投影。正交投影我们先做平移，再做缩放。我们把物体的中心移动到坐标轴远点，之后把物体限制在（-1，1）的立方体中。

**透视投影：**我们先把透视投影变换为正交投影所需的长方体，再进行正交投影。再压缩透视投影的梯形体时，对于前面的面上的点，z值不变，后面面上的点同理。

光栅化

采样

我们先忽略z轴，考虑-1，1的正方体。采样就是判断像素点是否在三角形内。我们可以对整个屏幕范围采样，也可以采用bounding采样，还有行bounding采样。

抗锯齿（反走样）

可见性（遮挡）

如何在采样的时候维持正确的模型顺序？–深度缓冲方法。该方法无法处理透明物体。如果两个三角形在同一个像素内有相同的深度如何处理？（工程实现问题）

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

着色与纹理

着色器可以做任何事情！！！

在本章节，我们只考虑着色点本身，不考虑其他点（比如遮挡）。每个着色点可以是一个像素，也可以是一个fragment，这取决于我们如何采样。I表示入色光的单位光强，V代表反色方向，n是法线。ivn都是单位向量。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

Blinn-Phong着色模型

该模型是一个经验模型。在该模型中，我们考虑漫反射，镜面反色和环境光。

漫反射diffuse：$L_d=k_d(I/r^2)max(0,nI)$。其中kd为漫反射系数（物体颜色），nI是光线和着色点的cos值。

镜面反射specular：$L_s=k_s(L/r^2)max(0,nh{)}^p,,,h=(v+I)/||V+I||$，H代表入i和v的半程向量，如果该半程向量与n很近，则代表人眼看到的高光越明显（为什么算半程向量，而不是算光的反色向量和人眼向量的sin，是因为半程向量计算简单）ks一般为白色。

环境光ambient:$L_a=K_a{I}_a$，该模型是一个经验模型，环境光当作一个常熟项简单处理。

最终着色：$L_d+L_s+L_a$

着色频率

1. 三角形着色，三角形法线可以用叉乘计算
2. 顶点着色，顶点法线可以用该顶点相关的三角形的法线的加权平均值。此外也可以用该顶点实际表示的图形来确定法线，例如如果用三角形组合表示圆，则顶点的法线防线可能是圆心到该顶点的连线方向。
3. 像素着色（fragemt），算出三角形的所有顶点法线，用插值方法得到像素法线。phong shadings

渲染管线

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

纹理

物体不同位置可能有不同的属性（着色时用特有的属性而不用同一的属性），该属性定义在物体表面上。我们把这个属性用一张图（纹理图）来表示，同时给出模型上每一个点对应纹理图上的点（纹理映射，纹理坐标一般定义在三角形的顶点上）。

**纹理太小：**映射道德如果是纹理中的非整数坐标，我们可以采用该顶点周围的四个点进行双线性插值，用差值，返回插值后的属性。

**纹理太大：**纹理太大时会导致采样频率不足，从而产生走样。不同像素覆盖纹理的区域不同，有些点可能实际覆盖了很大一部分纹理区域，只返回该点的属性必然会导致走样问题。可以通过范围查询方法MipMap来缓解。范围查询返回一定范围内的平均值，MipMap是一种近似方法，fast,approx，square。该方法在远距离下会导致过度模糊。

MipMpa方法

该方法会提前计算4和1，8和1，，，，点的平均值，并保存$lo{g}_{2}h$个纹理图。其中h是正方形纹理的长度。

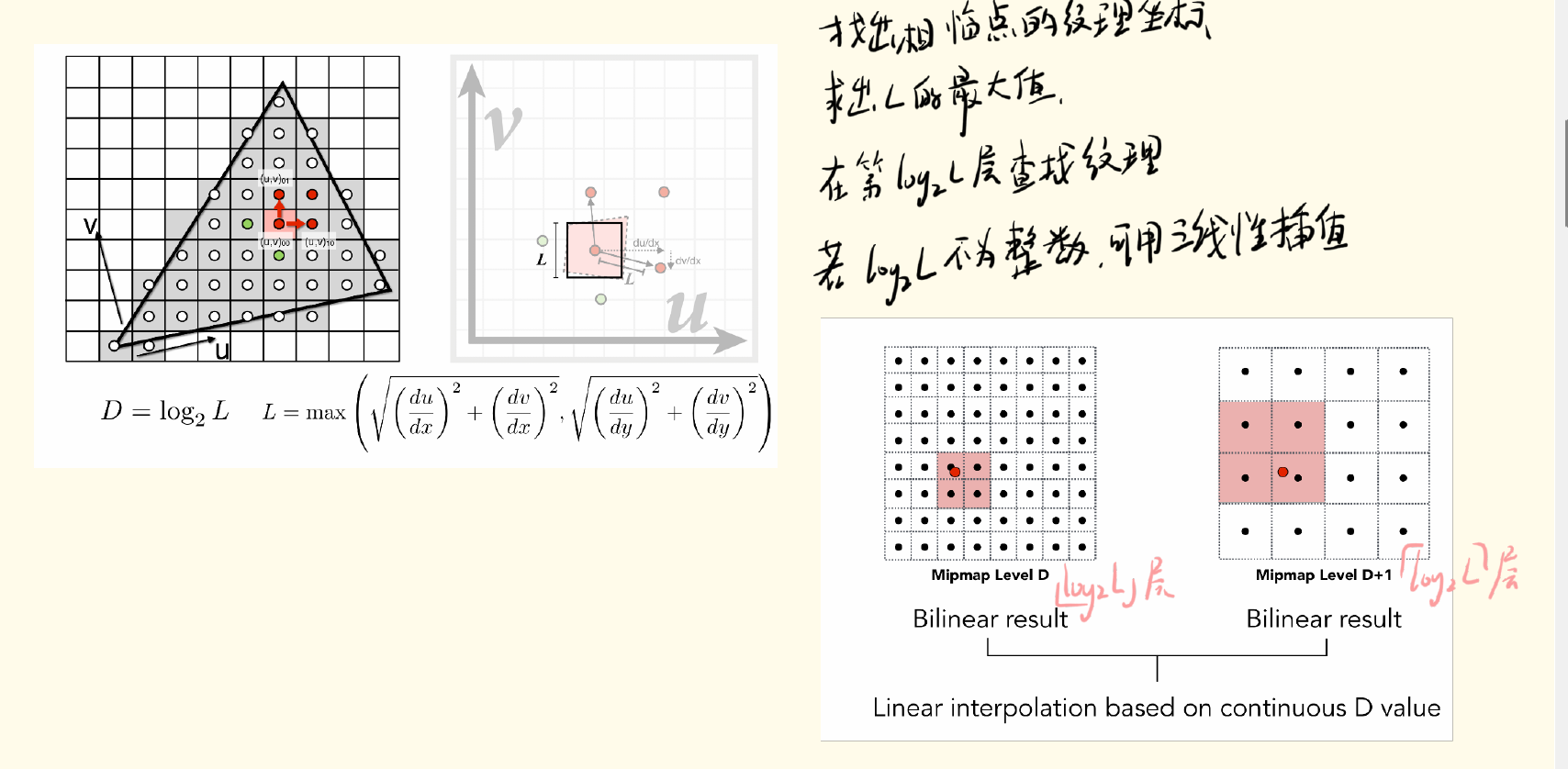
在进行纹理映射时，我们首先确定每个点所覆盖的纹理范围。我们通过该点周围的四个点的坐标来把纹理覆盖范围近似成正方形。通过纹理覆盖范围的边长查找相应层级的纹理图。如果log2L不为整数，我们可以在两层纹理图中采用三线性插值的方式得到最终属性。

MipMap方法无法解决该点所覆盖的纹理是矩形（尤其是长条矩形）情况下的的走样问题。一种缓解方法是各向异性过滤。该方维护不同长宽比例下的纹理分层图。

如果要缓解倾斜矩形，可以采用EWA filtering方法，但是该方法计算量大。

纹理作用

**环境光纹理：**纹理可认为是gpu中的一块数据，可以做点查询和范围查询。因此我们可以把环境光做成纹理，渲染过程中通过纹理映射仿照环境光。我们可以用一个光滑的球体来记录环境光，把球展开贴到环境中的物体表面。用球有个缺点是极点初会被压缩。为了解决这个问题，我们可以用一个正方体包围一个球体。把球体上的每一个点都沿着法线方向打到立方体表面。

**凹凸贴图：**凹凸贴图定义了每个点的相对移动距离，从而改变着色点的法线，渲染出一种凹凸的质感。实际上该点并不会凹凸。我们假设原始表面是水平，并且法线向上。在二维情况下更改后的法线如下图左图。我们通过推广，可以得到三位空间下更改后的法线，下图右图。（纹理保存的是高度变化信息h）。注意在三位空间中，法线方向不一定为001,此时我们需要转换坐标系，在新的坐标系下法线方向为001，此时我们求出新坐标系下更改后的法线，再将该法线映射会原坐标系。

**三维纹理：**我们也可以定义一个三维空间的噪声函数来作为纹理。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

**环境光遮蔽纹理：**我们可以提前算出物体的环境光遮蔽，把他保存为纹理，加速实时渲染。