强化学习_PPO算法
定义:在强化学习框架中,智能体通过与环境交互来学习。在每一步,智能体根据当前的环境状态选择一个行动,然后环境会根据这个行动反馈一个新的状态和一个奖励给智能体。智能体的目标是通过这种交互过程来学习一个最佳策略,即一系列的行动,使得长期累积的奖励最大化。可以想象跟AI下围棋的过程
1.相关定义
state定义:比如说视觉就是一幅图像或者是一幅矩阵(模型的输入)

action定义:交互后的反应,例如选择上下左右(模型的输出,反作用于模型的下个输入state)
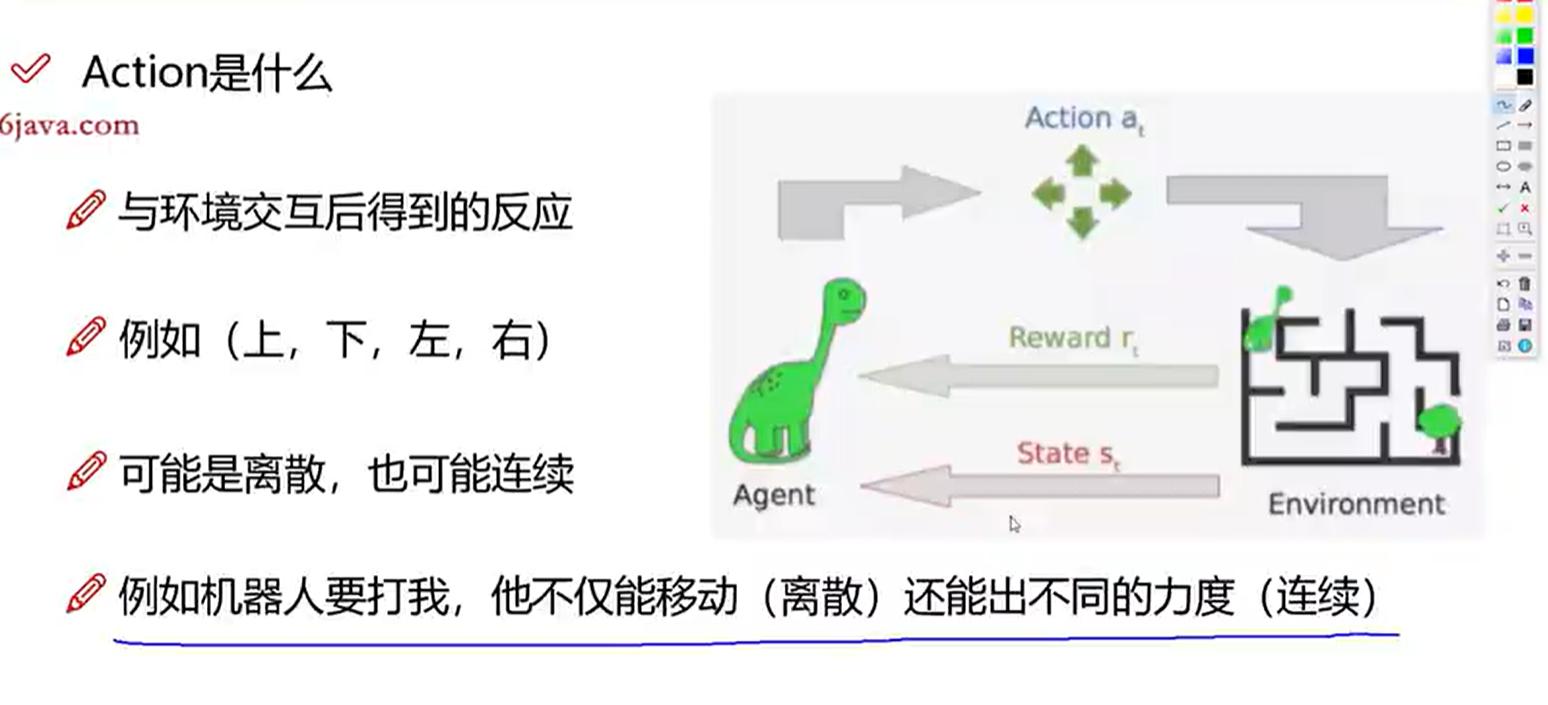
初步理解:如何得到state和action:比如以超级玛丽游戏为例子,由现在的图片(当前状态state)作为输入,来控制上下左右走的行动action,也就是输出
- 奖励(reward)背景:我们前面提到了超级玛丽的例子,提到了不同的行动,但是并没有说明那种行为更好,因此我们在此处引入了奖励
- 奖励(reward)定义:与环境交互得到奖励(用于得到不同的损失用于训练网络)
前面介绍了三个基本的内容 State Action 和 Reward,后面我们站在整个模型层面进行介绍:
- trajectory(轨迹
- ):包括一个完整的游戏过程中的state和action,比如说我们前面提到的超级玛丽,开始到登上小红旗通关
- 公式:
- 公式解释:
- 是在策略参数
- θ 下观察到整个轨迹 τ (轨迹包含内容见上一幅图片)的概率。
- 是初始状态
- 出现的概率,通常认为是环境给定的。
- 是时间步从1到T的乘积操作符,表示连乘所有时间步。
- 是在策略参数 θ 下,在时间步t给定状态 时选择动作
- 的概率(下面有解释)。
- 是在时间步t给定状态 和动作的情况下转移到状态
- 的概率,这是环境的转移概率。
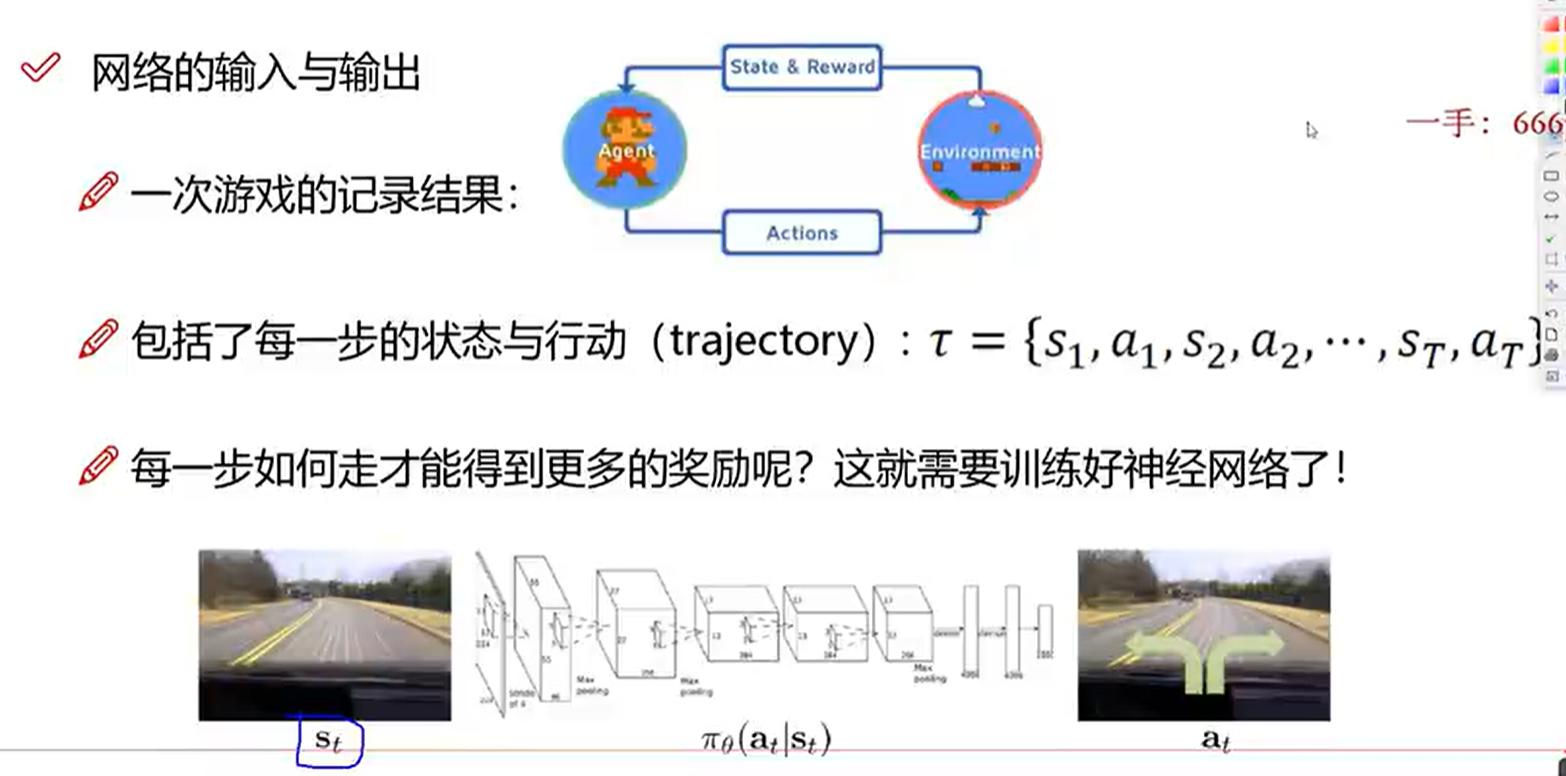
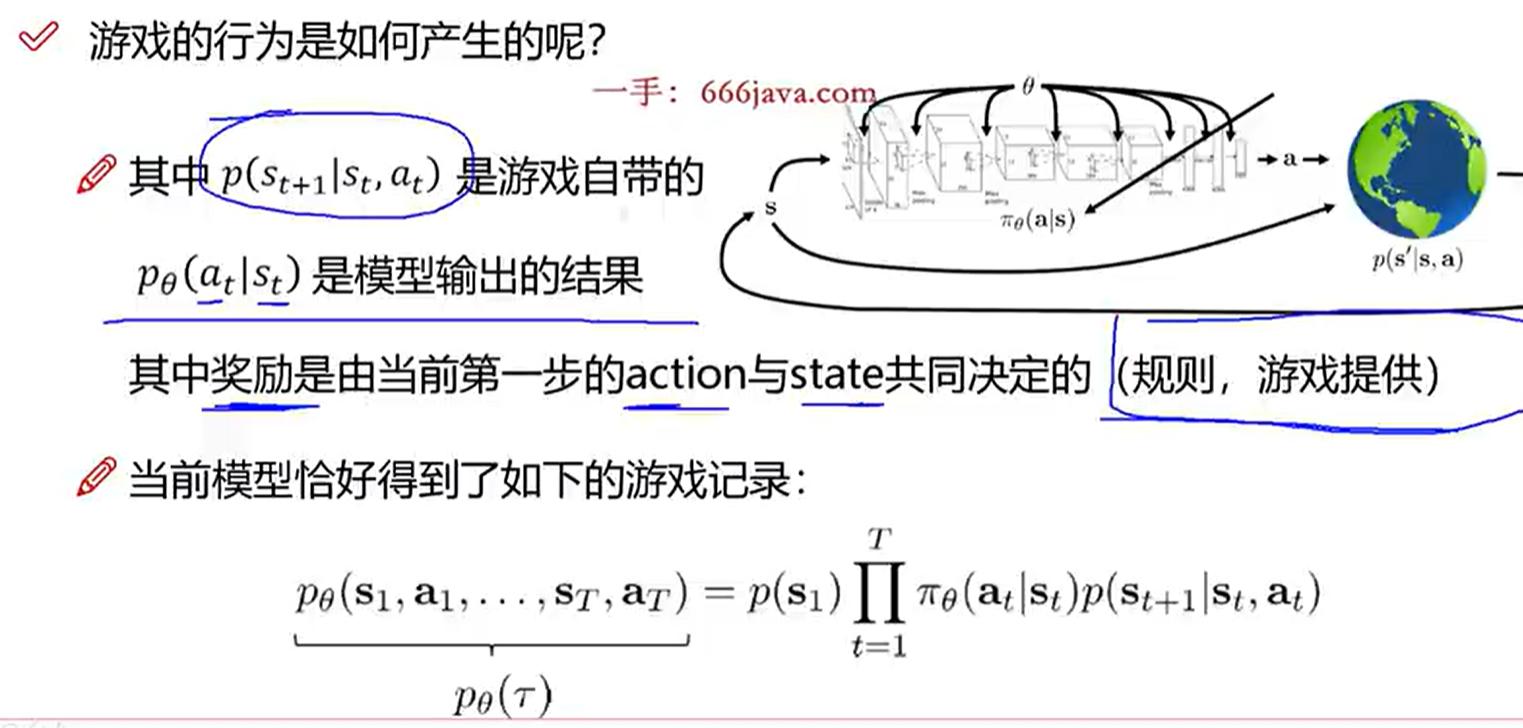
游戏的过程
我们可以通过一个强化学习的例子来解释
,假设你在训练一个自动驾驶的智能体在一个简单的十字路口环境中行驶。
- 1. 状态
- 可以表示智能体所在的位置(比如十字路口的某一条路上),周围是否有车辆行驶,红绿灯的状态等。
- 2. 动作
- :在给定状态
- 下,智能体可以执行的动作。比如在十字路口,智能体可以选择 “前进”、“左转”、“右转” 或 “停车”。
- 3. 策略
- :这个策略函数根据当前的状态 来输出执行每一个动作
- 的概率。例如:
- - 如果当前状态
- 是“绿灯且无车辆”,则智能体可能以高概率 前进
- 选择前进的动作。
- - 如果当前状态
- 是“红灯且有车辆靠近”,则策略函数可能给停车的概率较高, 停车
2.优化目标
优化目标:
是控制策略的参数。在 PPO 中,通过优化来找到一个最优的策略,使得智能体能够在环境中获得最大化的累积奖励。
- 1. 策略的定义: 假设策略
- 是神经网络的权重和偏置,它们决定了输入状态如何映射到动作的概率。
- 2.
- 的作用:如果
- 的值设置得合适,机器人在看到某些状态时可能更倾向于选择正确的动作,从而更快地找到终点并获得更高的奖励。
- 3. 策略更新:在训练过程中,PPO 算法会不断调整
- 的值(也就是更新神经网络的权重),让机器人在特定状态下更有可能做出获得奖励更高的动作。因此,
- 的值会随着训练迭代而改变,以便让机器人更有效地完成任务。

公式定义:定义了强化学习中的一个目标:找到一个策略参数 θ,使得期望的累积回报最大化。直观含义是:我们试图找到参数 θ,使得策略
在所有可能轨迹上的期望回报最大。具体来说:
- :这是我们想要找到的最优策略参数。
- :这表示我们的目标是找到能使后面的期望值最大化的参数 θ。
- :这是在策略
- 下产生轨迹 τ 的期望,表示我们对所有可能的轨迹进行平均。
- :这是在时间步 t 下,状态 和动作
- 对应的累积回报的总和
3.数学推导(可跳过)

- 公式含义:对于每一条采样的轨迹 i,计算它在每个时间步 t 的回报,然后对所有轨迹的总回报取平均,得到期望回报的近似值。
- 表示总共由N条路径,i代表选取的一种路径,每一个时间步 t 的平均值。
- 是在时间 t 通过采取动作 在状态
- 获得的即时奖励。
- 对于每一条轨迹 i,我们在每个时间步 t 上都计算对应的奖励,
- ,并在所有时间步上求和。
借助大数定律的思想:做i次实验(i是一个比较大的次数)来模拟穷去所有可能性

- 上图:(公式一)进一步定义目标函数
- :这是策略的性能函数,它表示了给定策略
- 下的期望回报。
- :这个期望表示所有可能的轨迹 τ(即状态和动作序列)的累积回报 的期望值。轨迹 τ 是由策略
- 产生的。
- :这是在一条轨迹中所有时间步的即时奖励 r 的和。它表示一个完整轨迹中从时间步 t=1 到 T 的累计奖励。
- :这是连续状态空间和/或动作空间中对所有可能轨迹的期望回报的积分形式。
上图(公式二):下面是对第二个求解梯度公式的说明,化成log函数求解(下图解释)

推导视频 : https://www.bilibili.com/video/BV1D5411B79i?t=13.3&p=11
- 上图公式
- (公式一):log函数求导定义
- (公式二):梯度符号
- 代表对参数 θ 的偏导数
- (公式三):利用log函数定义,将求解任务转变为对数求导。利用下面黄线可知,左右两式相等

- 上图公式
:这表示对策略性能函数
- 的期望回报进行梯度(导数)计算。这个梯度指出了参数 θ 应该如何改变来提升策略的期望回报。
- :这是对 N 个轨迹(或者说样本)的平均操作。每个轨迹 i 都是独立采样的,代表了策略
- 在环境中的一次完整执行。
- :这部分是对数概率的梯度,它衡量了在给定状态 下,采取动作
- 的概率的对数对参数 θ 的敏感度。通过取梯度,我们可以知道参数 θ 的哪些变化最可能增加这个对数概率。
- :这是从时间步 t=1 到 T 的第 i 个轨迹的所有即时奖励之和。

加入惩罚项:将绿色部分进行优化,可以理解为一个标准化操作,有正值有负值

4.On-OffPolicy策略
- 感性理解OnPolicy:利用一个模型与环境交互更替参数值
- 感性理解OffPolicy:在此处,我们利用两个网络模型,一个跟环境进行交互(模型A),而另一个跟模型A进行交互更替参数值,模型(B)

视频定位:https://www.bilibili.com/video/BV1D5411B79i?t=6.4&p=13
On policy为什么只会更新一次:在每次迭代中,基于当前策略产生的数据,只对策略参数进行一次更新。这是因为每一次策略的更新理论上都会导致策略的变化,进而影响后续数据的分布。为了准确计算期望值,理论上需要从更新后的策略中重新采样数据。("也就是这好像有麻烦了"的出处)

Importance Sampling操作:使用一个新的分布来代替旧的分布

公式一:理论部分,最初的分布为P
表示函数 在概率分布 下的期望值。它可以被理解为 加权平均值,其中每个值的权重由 给出。这个期望是对所有可能 值的
- 加权和的度量。
- 积分表达式
- 是期望值的连续形式的精确定义。当 取遍所有可能值的时候, 的值乘以它们发生的概率
- ,然后对整个空间积分。
- 是期望值的蒙特卡洛估计,它是对左边期望值的近似。在这种情况下,我们采用从分布 中抽取的 个样本 ,然后计算这些样本上函数 值的平均值。当 很大时,根据大数定律,这个平均值会趋于实际的期望值
- 。
公式二:图片的第二部分引入了重要性采样
,这是一个当直接从p(x) 采样困难或者不方便时使用的技术。
- 这里q(x) 是另一个概率分布,从这个分布采样通常比从p(x) 采样更容易或者更高效。关键在于,当你用q(x) 来生成样本时,你必须使用一个权重 q(x)p(x) 来调整每个样本的贡献,使得最终的估计是无偏的。
- .在这里,你从 分布中采样N 个样本 ,然后计算加权平均,其中权重是 。这个方法允许我们用一个辅助分布
- 来有效估计在分布 P(x) 下的期望值。


策略 πθ 下关于轨迹 τ 的分布计算的。这里的 τ 代表了从开始到结束的一个完整的状态-动作序列。r(τ) 表示这条轨迹的回报。
PPO算法整体思路解析:https://www.bilibili.com/video/BV1D5411B79i?t=453.0&p=15
5.实例说明
PPO实战-月球登陆器训练实例

Critic表述的就是绿色部分的公式,用于在不同的阶段打不同的怪
- 表示目标函数J(θ)相对于策略参数θ的梯度。
- 近似符号≈表示真正的梯度通常是无法直接计算的,所以我们使用有限数量的样本来估计它。
- 是对N个轨迹或者说是剧情的平均。
- 从i=1到N的求和表示对N个采样轨迹的平均。
- 从t=1到T的求和在单个轨迹内部按时间步进行累加。T可能是每个轨迹的长度。
- 是策略概率的对数的梯度,这在策略梯度方法中是常见的项,因为取对数的梯度可以简化数学运算。它衡量了在状态 下,采取动作
- 的对数概率的改变如何影响策略参数θ。
- 是在状态s_i,t采取动作a_i,t后所得到的奖励。
PPO2版本公式解读

- :这是PPO的目标函数,我们的目标是找到参数 θ 使这个函数最大化。
- )
- :这是优势函数的估计,表示在状态 st 采取动作 at 相对于平均值的好处。优势函数的估计通常通过一些方法计算得出,例如通用优势估算 (GAE)。
- :这是新策略 p_θ 相对于旧策略 pθk 在动作 at 上的概率比例。这个比例也被称作“重要性采样比例” (importance sampling ratio)。
- :这是PPO特有的“截断策略比例”,其中 ϵ 是一个小常数,例如0.1或0.2。这个clip函数确保了重要性采样比例在 [1−ϵ,1+ϵ] 的范围内,这样可以避免策略更新太大。
代码:
#整体
self.policy = ActorCritic(state_dim, action_dim, n_latent_var).to(device)
self.optimizer = torch.optim.Adam(self.policy.parameters(), lr=lr, betas=betas)
self.policy_old = ActorCritic(state_dim, action_dim, n_latent_var).to(device)
self.policy_old.load_state_dict(self.policy.state_dict())#ActorCritic
class ActorCritic(nn.Module):def __init__(self, state_dim, action_dim):super(ActorCritic, self).__init__()self.state_dim = state_dimself.action_dim = action_dim# 定义 Actor 网络结构self.actor = nn.Sequential(nn.Linear(state_dim, 128),nn.ReLU(),nn.Linear(128, action_dim),nn.Softmax(dim=-1))# 定义 Critic 网络结构self.critic = nn.Sequential(nn.Linear(state_dim, 128),nn.ReLU(),nn.Linear(128, 1))def forward(self, state):# Actor 网络输出动作概率分布action_probs = self.actor(state)# Critic 网络输出状态价值state_value = self.critic(state)return action_probs, state_value