大连理工大学选修课——机器学习笔记（6）：决策树

决策树

决策树概述

决策树——非参数机器学习方法

参数方法：

参数估计是定义在整个空间的模型

所有训练数据参与估算

所有的检验输入都用相同的模型和参数

非参数方法：

非参数估计采用局部模型

输入空间被分裂为一系列可以用距离度量的局部空间
每个输入只使用邻近区域由训练样本计算得到的局部模型

决策树特点

1. 采用分治策略

   • 简洁高效可并行
   • 递归

2. 输入空间被描述为一种树形结构

   • 层次递归
   • 内部结点：决策节点
   • 叶子结点：决策结果，可做分类，也可做回归分析

   

决策树方法简介

→每个结点的决策函数都是定义在d维空间的判别式

• 将空间有效地分为较小区域

• 子结点对父结点确定的区域进一步分裂

• 每个结点的决策函数是一个简单函数

  • 不同的函数确定不同的判别式形状和区域形状

  

→可以快速确定输入的区域

• 对于二值分类，每次决策可以排除一半的实例
• 如果是$k$个类别，可在$lo{g}_{2}k$次决策后找到答案

→可解释性好

• 可写成容易理解的决策规则

构建决策树

决策树的构建方法

→只采用一个输入维

• 处理离散变量
  • 根据属性值的多少确定分支数量
  • 如果是连续数值，则离散化处理
• 处理连续变量
  • 根据数值确定阈值：$f_m(x):x_j>w_{m0}$
  • 将空间一分为二

→构造一棵决策树

L m = { x ∣ x j > w m 0 } R m = { x ∣ x j ≤ w m 0 } 两个区域相互正交，叶子节点定义输入空间的矩形 L_m=\{x|x_j>w_{m0}\}\\ R_m=\{x|x_j\leq w_{m0}\}\\ 两个区域相互正交，叶子节点定义输入空间的矩形 Lm​={x∣xj​>wm0​}Rm​={x∣xj​≤wm0​}两个区域相互正交，叶子节点定义输入空间的矩形

→单变量决策树：每次分裂只用一个特征

• 根据训练样本构造的决策树，称为树归纳。

• 给定的训练集可以构造很多的编码树，要找到最优树：

  • 节点数量
  • 决策函数复杂度
  • NP完全问题

  →通常采用贪心算法

单变量决策树的构建问题

→多特征样本在构建时的特征变量选择

• 不同的变量分裂结果不同
• 离散/连续变量分裂也存在差别

→何时分裂会得到最终结果？

• 没有特征变量时，分裂自然终止
• 如果还存在可用的特征变量，是否继续分裂？

→建立决策树过程中的评价方法

• 熵和定义基于熵的评价指标
• 基尼系数
• 分类误差

ID3算法

输入输出

输入:

• 训练数据集$D$，包含若干样本,每个样本有$d$个特征和一个类别标签。
• 特征集 A = { A 1 , A 2 , ⋯ , A d } A=\{ A_1,A_2,\cdots,A_d \} A={A1​,A2​,⋯,Ad​}。
• 目标属性（类别标签）$C$。

输出：一棵决策树。

算法步骤：

1. 检查终止条件

   满足以下任意条件，停止分裂，返回叶子结点：

   1. 所有样本属于同一类。
   2. 无剩余特征可用。
   3. 样本集为空（极少发生）。

2. 选择最优分裂特征

   对剩余特征逐个计算信息增益，选择增益最大的特征作为当前结点的分裂特征：

   1. 计算数据集的熵

      $$Entropy(D)=-\sum _{k=1}^K{p}_{k}lo{g}_2{p}_k$$

   2. 计算特征$A_i$的信息增益

      $$IG(D,A_i)=Entropy(D)-\sum _{v\in Values(A_i)}\frac{|D_v|}{|D|}Entropy(D_v)$$

      $Values(A_i)$：特征$A_i$的所有可能取值。

      $D_v$：$D$中$A_i=v$的子集。

   3. 选择信息增益最大的特征

$$A_{best}=argmaxIG(D,A_i)$$

1. 按特征值分裂数据集

   根据$A_{best}$的取值，将$D$划分为若干子集$D_v$，每个子集对应一个分支。

• ID3算法存在的问题
  • 只能处理离散属性
  • 更多值属性偏向问题：当一个属性具有大量可能值时，ID3算法倾向于选择该属性进行分裂，即使它可能不是最有信息量的属性。如：ID号可能会被优先选择，因为它的可能值很多。

C4.5算法

• 改进：
  • 连续属性的离散化
  • 解决多值属性的偏向

    • 信息增益计算的标准化

      引入增益率，通过特征的固有信息对信息增益进行归一化：

      $$\begin{gathered} I_R(D,A)=\frac{I(A,D)}{H_A(D)} \\ （H_A(D)=-\sum _{i=1}^n\frac{|D_i|}{D}lo{g}_2\frac{|D_i|}{D}） \end{gathered}$$

      $I_R(D,A)$：增益率。

      $H_A(D)$:固有信息，衡量特征$A_i$的取值分布的均匀性。

      其中n为特征 A 的类别数， Di为特征 A的第i个取值对应的样本个数，|D| 为样本个数。

CART算法

• 特点

  • 使用基尼系数选择分裂用的最优特征
  • 建立的决策树是二叉树

• 基尼系数的计算

  假设有K个类别，第k个类别的概率为pk , 则基尼系数的表达式为：

  

  对于二值分类：

  

  对于样本D，如果根据特征A的某个值a，把D分成D1和D2两部分，则在特征A的条件下，D的基尼系数表达式：

  

  对于个给定的样本D，假设有K个类别，第k个类别的数量|Ck|为，则样本D的基尼系数表达式为：

  

• 连续属性的离散化处理
  处理思路与C4.5一样，衡量的标准是基尼系数，连续属性还会参与后续的结点分裂

• 二叉树的实现
  找到基尼系数最小的二分结果
  例如{A2}和{A1, A3}，建立二叉树
  后续还有机会对结点{A1, A3}按照特征A进行分裂

• 算法描述
  算法输入是训练集D，基尼系数的阈值，样本数量的阈值输出是决策树T

1. 对于当前结点的数据集为D，如果样本个数小于阈值或者没有特征，则返回决策子树，当前结点停止递归；
2. 计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前结点停止递归；
3. 计算当前结点现有的各个特征的各个特征值对数据集D的基尼系数；
4. 在计算出来的各个特征的各个取值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的取值a。根据这个最优特征和最优值，把数据集分裂成两部分D1和D2，同时建立当前结点的左右结点，左结点的数据集为D1，右结点的数据集为D2；
5. 对左右的子结点递归的调用1-4步，生成决策树。

• 特殊处理

  CART的叶子结点的不纯性不一定降到最低：叶子结点中的样本可能会属于多个类
  在用CART树做预测时，选择训练样本所占比例最大的类别作为预测结果
  或者在构建决策树时，将叶子结点的类别标签选择为比例最大的训练样本类别

• 建立回归树

  • ID3和C4.5只建立分类树
    这一点限制了两个算法的使用范围
  • CART的长处除了计算量小以外，还有该算法既可以做分类又可以做回归
  • CART的回归树和分类树大同小异
    回归的输出是连续的
    设置为到达该结点所有样本实例输出的均值
    分裂属性选择的衡量标准是分类误差

• 均方误差度量
  定义二值化的指示函数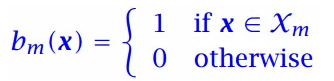

  

  结点m的预测输出：

  

  结点m的误差：

  

• 分裂的操作
  如果结点m的误差太大，不能接受（根据预设的阈值判断），需要对结点进行分裂
  在众多选的分裂结果中选择诸分支误差和最小的，每次递归的分裂都是得到二分的结果
  对于结点m的分支 j：

  

  分裂后的总误差：

  

• 误差阈值

  • 调节模型复杂程度的超参数

  • 图片为误差阈值降低后树的变化

    

    

    

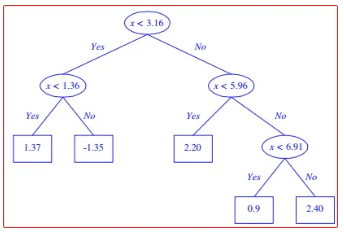
    过拟合

过拟合问题：不要期望把结点的不纯性降到最低，小于某个阈值即可

剪枝

• 先剪枝

到达一个结点的实例数小于训练集的某个百分比（设个阈值，例如5%），然后就停止该结点的进一步分裂。速度快，但效果不是很理想。

• 后剪枝

先让树完全增长至零训练误差或者结点不纯性降到最低，然后剪掉导致过拟合的子树。
后剪枝是全局搜索，效果更好，但会很慢。

几种量化结点纯度的指标对比

                          基尼系数是熵的一个很好的近似

熵与信息增益

熵的概念

——熵度量了事物的不确定性

• 越不确定的事物，熵越大

• 随机事件X的熵定义：

  $$H(X)=-\sum _{i=1}^n{p}_{i}log{p}_i$$

• 联合熵：

$$H（X,Y)=-\sum p(x_i,y_i)logp(x_i,y_i)$$

• 条件熵

$$H(X|Y)=-\sum p(x_i,y_i)logp(x_i|y_i)=\sum p(y_j)H(X|y_j)$$

信息增益

• 信息增益也称为互信息
• 定义如下：

$$I(X,Y)=H(X)-H(X|Y)$$

计算实例：

树结点度量指标

→度量结点的不纯性

• 用熵描述结点m的不纯性

  $$I_m=H(C)=-\sum _{i=1}^K{p}_m^{i}log{p}_m^i$$

  $p_m^i$表示第$i$类样本所占比例

  如果结点不需要分裂（到达结点m的所有实例只属于一个类别C，没有不确定性），则不纯性$I_m=0$，即$H(C)-0$。

• 子结点不纯性的计算

  假设父节点$m$的离散属性有n个取值，即有n个输出

  • 连续属性有两个输出$(n=2)$，有如下统计：

  $$\sum _{j=1}^n{N}_{mj}=N_m$$

  $N_{mj}$个实例中有$N_{mj}^i$个属于类$C_i$

  $$\sum _{i=1}^K{N}_{mj}^i=N_{mj}\sum _{i=1}^n{N}_{mj}^i=N_m^i$$

  $$\hat{p}(C_i|x,m,j)=p_{ml}^i=\frac{N_{mj}^i}{N_{mj}}$$

  n个子结点的总不纯度为：
  

分裂选用的特征

• 每次分裂需要选择特定的属性进行

  • 选择的策略：

    • 能使不纯度下降最大的属性：

      $$I_m-I_m^{AH}$$

    • 能使信息增益最大的属性

      两个随机变量之间的统计依赖性或信息共享程度

      衡量已知一个变量的信息后，另一个变量的不确定性减少的程度

    $$I(X_m,C_{mj})=H(X_m)-H(X_m|C_{mj})$$

连续属性的处理

• 通常，构建决策树时只考虑使用离散属性
• 而连续属性需要转换成只有两个取值的离散属性
• 可以选择使用所可能取值的平均值/均值作为阈值。

决策树C4.5算法的处理

设样本的连续属性有m个不同取值，将所有取值排序，取所有相邻的两个值，计算他们的均值，从而得到$m-1$个均值，将它们作为候选阈值。测试用每个阈值分裂二值结果的互信息，选择能带来最大互信息的均值作为最后的阈值进行二值分裂。

使用决策树

• 决策树的每一条从根到叶子的路径：对应的条件的合取（AND）。

• 对于分类树，可能有过个叶子被标记为相同的类：多个路径对应的条件用析取（OR）。

• 各个路径可以用IF-THEN规则表示

  

几种经典模型的对比

| 算法 | 支持
模型 | 树结构 | 特征选择 | 连续值
处理 | 缺失值
处理 | 剪枝 |
| — | — | — | — | — | — | — |
| ID3 | 分类 | 多叉树 | 信息增益 | 不支持 | 不支持 | 不支持 |
| C4.5 | 分类 | 多叉树 | 信息增益比 | 支持 | 支持 | 支持 |
| CART | 分类，
回归 | 二叉树 | 基尼系数，
均方差 | 支持 | 支持 | 支持 |

决策树模型评价

• 优点

1）简单直观，生成的决策树很直观

2）基本不需要预处理，不需要提前归一化

3）相比于神经网络之类的黑盒分类模型，决策树在逻辑上
可以得到很好的解释

4）可以交叉验证的剪枝来选择模型，从而提高泛化能力

5）对于异常点的容错能力好，健壮性高。

• 缺点

1. 决策树算法非常容易过拟合，导致泛化能力不强

• 通常把决策树用作基准模型（baseline）
• 或作为集成学习的弱学习模型

2. 决策树会因为样本发生一点点的改动，就会导致树
   结构的剧烈改变
3. 寻找最优的决策树是一个NP难的问题，我们一般是
   通过启发式方法，容易陷入局部最优。

总结

• 每个类可能存在对各分支对应的多个解释和描述
  • 这些不同的解释可能会在空间中不相交
• 不必考虑各个区域（特征子空间）上的分布信息
  • 直接对分离类实例的判别式进行编码
• 属于基于判别式的（discriminant-based）方法
• 更多地应用于分类