当前位置：首页 > backend >正文

前缀和和差分思路理解以及典题题解

backend 2025/9/5 9:33:51

前言

笔者是ACM选手，已经学习了一段时间算法，苦苦刷完大神拉的算法题单，感觉前缀和和差分是最简单的，所以想要写一篇理解前缀和和差分的文章，并为我刷的题单写题解，以检验对算法的掌握程度

本篇文章讲述了一维、二维前缀和和差分的思路以及代码实现，还会附一道典题题解，完全不会前缀和的读者也可以阅读

一维前缀和

（1）思路理解

一维前缀和数组存储的是一维数组前n个数的和，举一个简单的例子可以让大家看到显著的效率提升：

1 2 3 4 5 6，这个数组，要算出第二位到第四位、第三位到第六位、第一位到第五位……等等位的数之和，朴素版代码应当是这样的：

vector<ll>num{1,2,3,4,5,6};ll sum=0;for(int i=1;i<4;i++){sum+=num[i];}sum=0;for(int i=2;i<5;i++){sum+=num[i];}sum=0;for(int i=0;i<6;i++){sum+=num[i];}sum=0;

也就是每次求的时候，都一次一次遍历，再累加

如果数据很小这样做没问题，但是N如果到了1e7那个地步，这样算的话将会非常慢

前缀和的效率暂且不说，先说思路：

前缀和用到一个代码里非常重要的“预处理”思想，即提前将数据处理，进而大幅度减轻后续的负担。

核心思路是开一个数组，与原数组下标对应，前缀和数组下标存的是原数组前i个元素之和

即：第一个元素存原数组第一个元素，第二个元素存原数组前两个元素之和，第三个元素存原数组前三个元素之和……

那么这样做有什么用呢？试想一下，第二位到第四位的元素之和，是不是前四位元素之和减去前一位元素之和？第三位到第六位元素之和，是不是前六位元素之和减去前两位元素之和？

由此我们便得出了前缀和数组的用法：

sum[2-4]=sum[4]-sum[1]，sum[3-6]=sum[6]-sum[2]

由此可以看到，前缀和的时间复杂度是O(n)，后续只需要O(1)的减法即可，非常快

那么这个前缀和数组怎么用代码实现呢？

很明显，前i个元素之和等于前i-1个元素之和加上第i个元素的值，所以sum[i]=sum[i-1]+arr[i]

（2）代码实现

使用代码完整实现一次：

vector<ll>num(7);for(int i=1;i<=6;i++){cin>>num[i];}vector<ll>sum(7);for(int i=1;i<=6;i++){sum[i]=sum[i-1]+num[i];}cout<<sum[4]-sum[1]<<endl;cout<<sum[6]-sum[2]<<endl;cout<<sum[5]-sum[0]<<endl;

注意：因为前缀和涉及到很多i-1操作，所以为了方便，我们直接设定起始下标是1，0下标为0，也不对后边造成干扰

（3）典题题解——求区间和

题目出处：P8218 【深进1.例1】求区间和 - 洛谷

思路：这道题完全就是一维前缀和的模板题，输入所有数据，计算前缀和，然后每次输入l和r处理即可

AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;void solve() 
{ll n;cin>>n;vector<ll>arr(n+1);for(int i=1;i<=n;i++) cin>>arr[i];ll m;cin>>m;vector<ll>s(n+1);s[1]=arr[1];for(int i=2;i<=n;i++){s[i]=s[i-1]+arr[i];}while(m--){ll l,r;cin>>l>>r;cout<<s[r]-s[l-1]<<endl;}
}int main() 
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while (t--) {solve();}return 0;
}

（4）常用技巧——使用前缀和判断括号串

直接上题目：

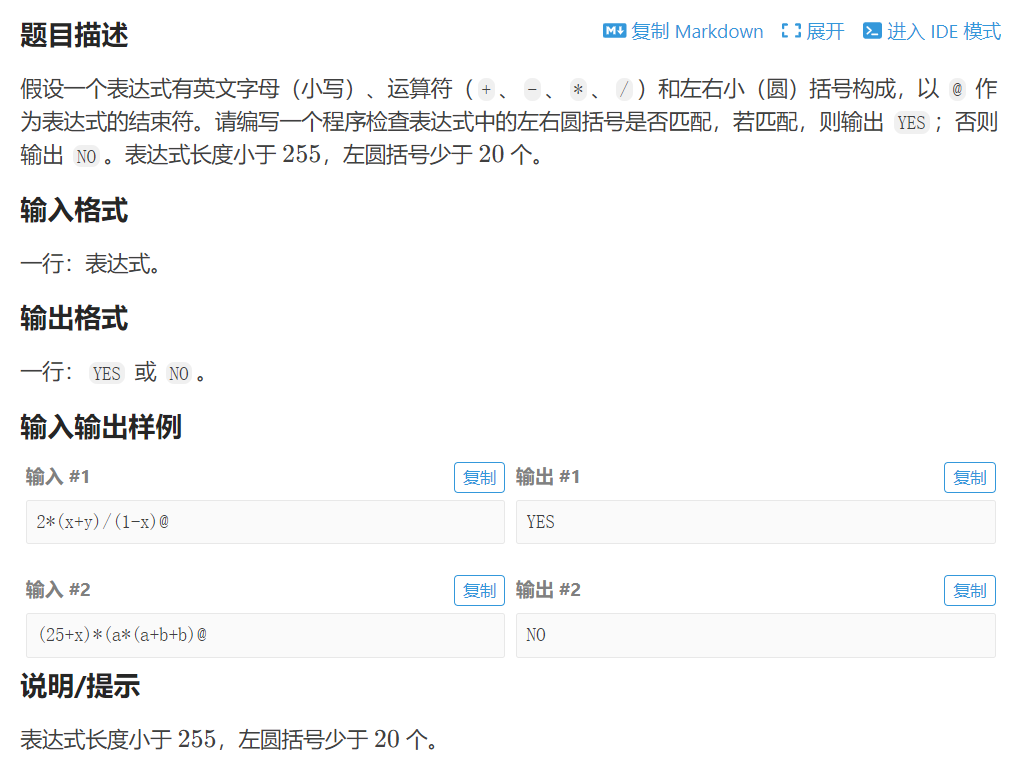
题目出处：P1739 表达式括号匹配 - 洛谷

暴力做法是一遍一遍搜，非常慢且不优雅，前缀和有一个很常用的技巧：设"("的权重是1，")"的权重是-1，扫一遍字符串，如果前缀和小于0，说明有一个")"没有对应的"("，如果最终前缀和不等于0，说明肯定数量不对应，也是不匹配。如此只需要扫一遍即可

AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;void solve() 
{string s;cin>>s;ll sum=0;for(int i=0;i<s.size();i++){if(s[i]=='('){sum++;}if(s[i]==')'){sum--;}if(sum<0){cout<<"NO"<<endl;return;}}if(sum!=0){cout<<"NO"<<endl;return;}cout<<"YES"<<endl;
}int main() 
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while (t--) {solve();}return 0;
}

使用前缀和处理括号串是一个很常用的做法

二维前缀和

（1）思路理解

二维前缀和和一维前缀和的作用一样，存的是二维数组元素之和。

还是使用一个例子来引入：

有这样一个矩形：

1 -2 3 -4 5

5 -3 2 -4 -1

4 -5 -6 3 2

要求出所有可能存在的矩形中元素之和最大的部分，画个图方便大家理解题意：

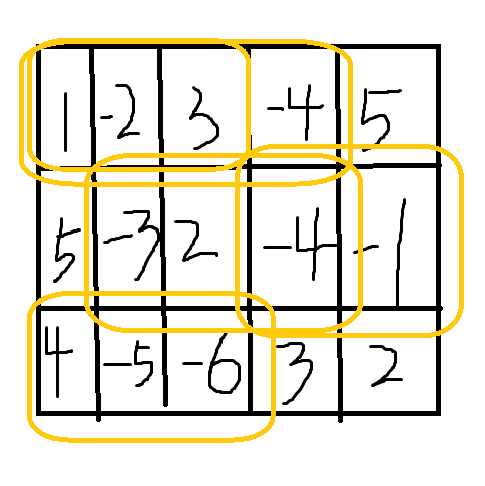
在这个大矩形中可以任意圈数字，像黄色圈住的一样，要求找到这样能圈住的有最大元素之和矩形

有没有暴力思路？

可想而知，如果暴力做的话，一定是相当慢且非常麻烦的。

所以我们再用一下刚才一维前缀和的思路，使用s[i][j]存从(0,0)到(i,j)的矩形面积大小，那么任意的矩形面积都可以算出来了。

我们先推出s[i][j]的求法：首先s[1][1]一定是arr[1][1]，s[i][j]的求法也可以通过递归的思想，通过已经求出的s数组存的内容来算

再画个图表示：

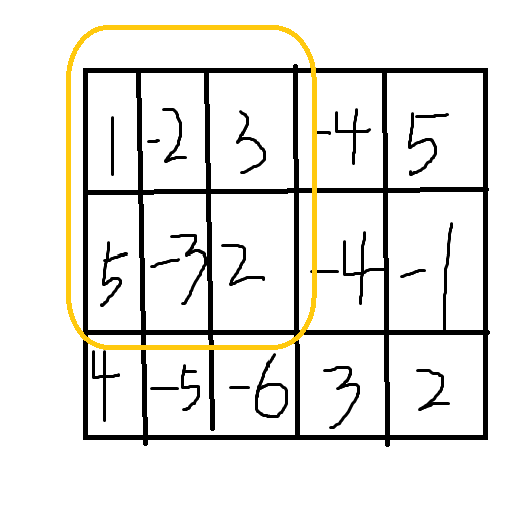
我们想算图中黄笔圈住的部分怎么做呢？这个部分是s[2][3]，首先我们要想清楚：s数组的遍历一定是下标从小到大的，也就是说算到s[2][3]的时候s[1][2]、s[2][1]这些下标更小的部分一定是已经算出来的，所以我们可以直接用这些数据。

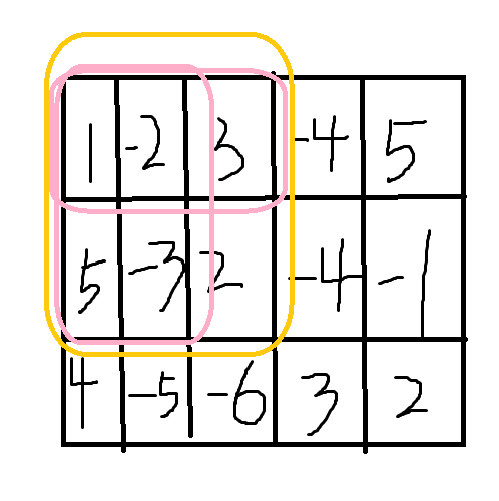
图中粉笔圈住的部分比当前要求的要小，一定是已经求好的。我们可以观察到这两个部分加起来，再减去重叠部分，再加上arr[2][3]，直接就是黄笔圈住的面积了。

所以s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+arr[i][j]

使用这个普适的式子，我们可以尝试从s[1][1]这个已知点遍历来证明其正确性，s[1][2]=s[0][2]+s[1][1]-s[0][1]+arr[1][2]，因为带0下标的都是0，不会对前缀和造成影响，所以s[1][2]=s[1][1]+arr[1][2]，依次往后推，会发现每个点都可以正确计算

如果这里你理解了，那么二维前缀和你已经理解了一半

另一半就是例子中的问题了：计算任意矩形的元素之和

比如图中这个黄色圈住的部分怎么算呢：

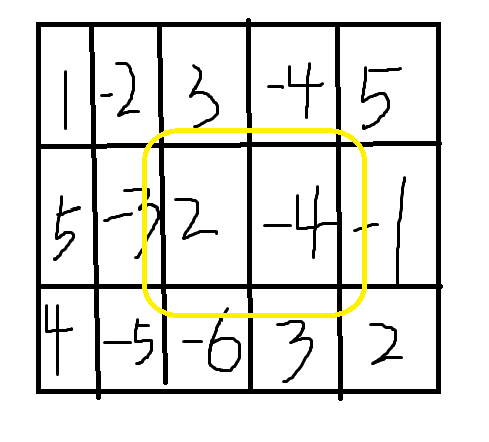
注意我们没有上帝视角，可以直接2+（-4），我们能用的只有s数组，即我们只知道从（1，1）到(i,j)的面积，我们可以这样算：

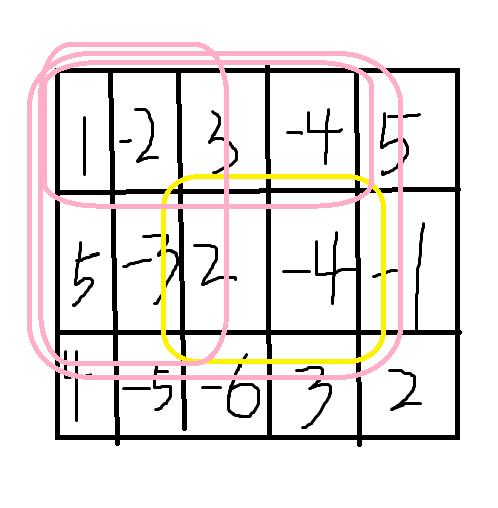
有三个用粉笔圈住的部分，这三个部分分别是s[2][4]、s[2][2]、s[1][4]，很容易可以观察到，使用这个大矩形减去两个小矩形，再加上小矩形重叠的部分，就是我们要求的黄色矩形内的元素之和。

（2）代码实现

s[1][1]=arr[1][1];for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){s[i][j]=s[i-1][j]+s[i][j-1]+arr[i][j]-s[i-1][j-1];}}

（3）典题题解——求最大加权矩形

题目出处：P1719 最大加权矩形 - 洛谷

思路：这道题和我刚才举的例子完全是一回事，观察到n的范围只到120，所以循环多一些也没关系，所以“任意”矩形可以直接遍历边长来控制。

AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;void solve() 
{ll n;cin>>n;vector<vector<ll>>arr(n+1,vector<ll>(n+1));for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>arr[i][j];}}vector<vector<ll>>s(n+1,vector<ll>(n+1));s[1][1]=arr[1][1];for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){s[i][j]=s[i-1][j]+s[i][j-1]+arr[i][j]-s[i-1][j-1];}}ll maxNum=s[1][1];for(int x=1;x<=n;x++){for(int y=1;y<=n;y++){for(int i=x;i<=n;i++){for(int j=y;j<=n;j++){maxNum=max(maxNum,s[i][j]+s[x-1][y-1]-s[x-1][j]-s[i][y-1]);}}}}cout<<maxNum<<endl;
}int main() 
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while (t--) {solve();}return 0;
}

一维差分

（1）思路理解

开门见山，差分就是前缀和的逆运算，用非常直观的式子来讲解：

前缀和是s[i]=s[i-1]+arr[i]，那么差分就是p[i]=arr[i]-arr[i-1]

将这两个式子移项，得到arr[i]=s[i]-s[i-1]，arr[i]=arr[i-1]+p[i]

我们可以很清楚地看到，原数组是前缀和数组的差分数组，同时是差分数组的前缀和数组

因为差分数组完全就是通过前缀和数组推导出来的，所以它给人实际的感觉并不强烈，因此初学者可能理解不了差分。

理解不了也没有关系，我们只需要知道它的应用场景：

给定一段数据，现在要把其中若干段加n或减n

暴力做法就是一遍一遍扫，每一遍都计算一次，这样做在数据很大的情况下自然也很慢，差分在这里就可以极大提高效率

要理解差分为什么可以实现快速进行区间修改，就要牢记“差分的前缀和数组就是原数组”这一点

我们最后可以利用差分数组计算原数组，所以如果差分数组的某一处+n，那么原数组这一处后边所有元素都会+n，如果差分数组某一处-n，那么原数组这一出后边所有元素都会-n。

我们立刻就能想到，给定主数组的某一段起止位置，差分数组起始位置+n，结束位置-n，最后用差分的到的原数组这一段就+n，而对后续不会造成影响

差分起作用的方式就是：先用原数组得到差分数组，再根据要求对差分数组操作，再用差分数组得到原数组

（2）代码实现

vector<ll>d(n+1);for(int i=1;i<=n;i++){d[i]=m[i]-m[i-1];}while(p--){ll x,y,z;cin>>x>>y>>z;d[x]+=z;if(y<n){d[y+1]-=z;}}for(int i=1;i<=n;i++){m[i]=m[i-1]+d[i];}

（3）典题题解——区间修改

出处：P2367 语文成绩 - 洛谷

思路：这道题明显就是一个简单的区间修改，是差分的模板题，直接套模板做即可

AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;void solve() 
{ll n,p;cin>>n>>p;vector<ll>m(n+1);for(int i=1;i<=n;i++){cin>>m[i];}m[0]=1000000000;vector<ll>d(n+1);for(int i=1;i<=n;i++){d[i]=m[i]-m[i-1];}while(p--){ll x,y,z;cin>>x>>y>>z;d[x]+=z;if(y<n){d[y+1]-=z;}}for(int i=1;i<=n;i++){m[i]=m[i-1]+d[i];}sort(m.begin(),m.end());cout<<m[0]<<endl;
}int main() 
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while (t--) {solve();}return 0;
}

二维差分

（1）思路理解

二维差分自然是以平面为单位的修改，即一片一片修改

而区域修改也需要考虑终止影响的位置，在起始位置加上这个数，在横坐标相同纵坐标结束位置再减去这个数，纵坐标相同横坐标结束位置再减去这个数，然后再结束位置加上这个数抵消一次

画图来辅助理解：

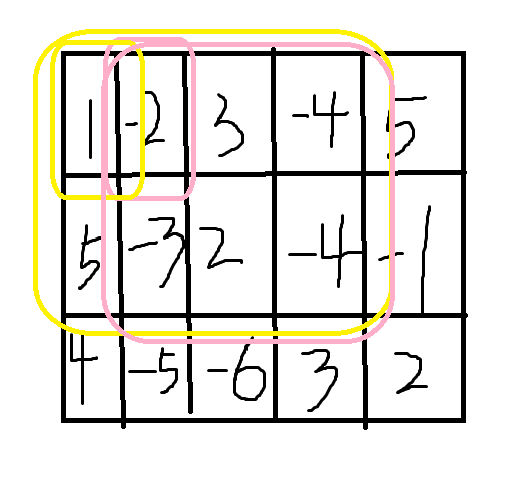
在左上角加1，变成-1，按照前缀和的算法计算，后续原数组所有位置都会+1，在粉圈右上角-1，右半部分就回归正常，在左下角+1，下半部分就回归正常，但是右下角位置减了两次1，所以需要+1

（2）代码实现

vector<vector<ll>>d(n+1,vector<ll>(n+1));while(m--){ll x1,x2,y1,y2;cin>>x1>>y1>>x2>>y2;d[x1][y1]+=1;if(y2<n) d[x1][y2+1]-=1;if(x2<n) d[x2+1][y1]-=1;if(x2<n&&y2<n) d[x2+1][y2+1]+=1;}vector<vector<ll>>s(n+1,vector<ll>(n+1));for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){s[i][j]=d[i][j]-s[i-1][j-1]+s[i][j-1]+s[i-1][j];}}

（3）典题题解——区域修改

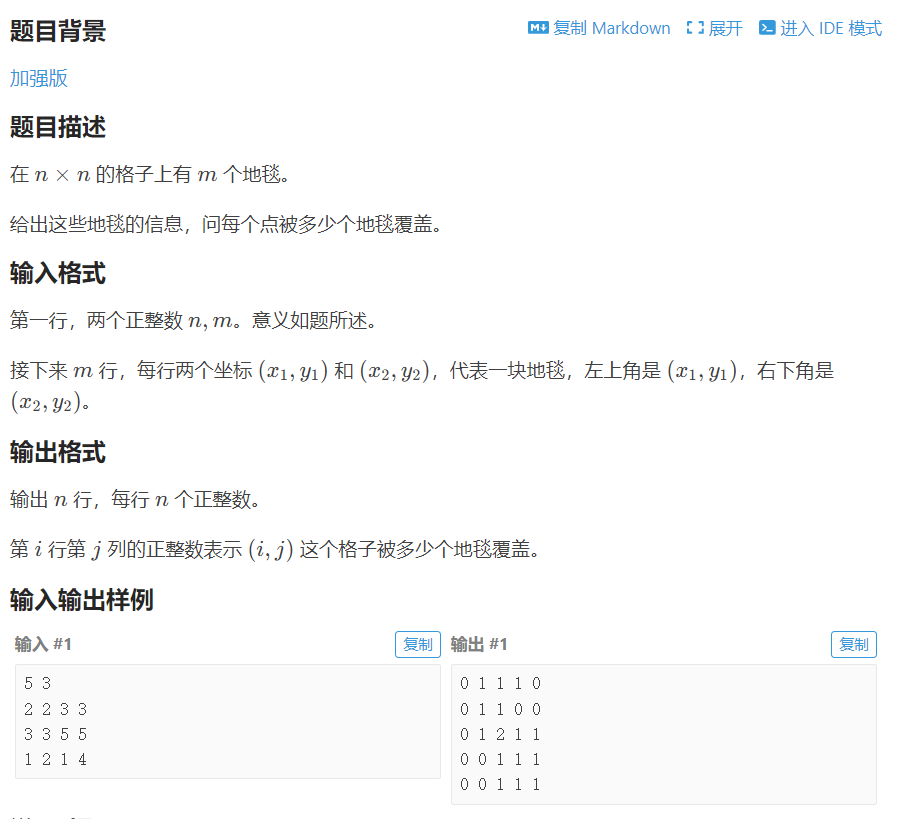
出处：P3397 地毯 - 洛谷

思路：n*n的矩阵，初始值全部为1，如果某一个地方有地毯，就+1，地毯是一片区域，所以要区域修改，因此用二维差分，很好做

AC代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;void solve() 
{ll n,m;cin>>n>>m;vector<vector<ll>>d(n+1,vector<ll>(n+1));while(m--){ll x1,x2,y1,y2;cin>>x1>>y1>>x2>>y2;d[x1][y1]+=1;if(y2<n) d[x1][y2+1]-=1;if(x2<n) d[x2+1][y1]-=1;if(x2<n&&y2<n) d[x2+1][y2+1]+=1;}vector<vector<ll>>s(n+1,vector<ll>(n+1));for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){s[i][j]=d[i][j]-s[i-1][j-1]+s[i][j-1]+s[i-1][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cout<<s[i][j]<<" ";}cout<<endl;}
}int main() 
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while (t--) {solve();}return 0;
}

变式题目

出处：P3406 海底高铁 - 洛谷

题意：有n-1条线，可以选择办卡再买票，花费是卡费+办卡后的票价*次数；也可以选择直接买票，花费是办卡前的票价*次数，问总共的最小花费

这道题的核心在于计算每条线的使用次数，从a到b，小的那个站到大的那个站区间内所有线次数均需+1，也是区间修改，可以用一维差分来做，统计出数据贪心一下，每条线选择最小花费即可

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;void solve()
{ll n,m;cin>>n>>m;vector<ll>p(m+1);for(int i=1;i<=m;i++) cin>>p[i];vector<ll>a(n),b(n),c(n);for(int i=1;i<=n-1;i++){cin>>a[i]>>b[i]>>c[i];}vector<ll>tp(n+1);vector<ll>num(n+1);for(int i=1;i<m;i++){ll t=p[i];ll s=p[i+1];if(t<s){tp[s]--;tp[t]++;}else{tp[s]++;tp[t]--;}}for(int i=1;i<n;i++){num[i]=num[i-1]+tp[i];}ll sum=0;for(int i=1;i<n;i++){ll x=min(num[i]*a[i],c[i]+num[i]*b[i]);sum+=x;}cout<<sum<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);ll t=1;//cin>>t;while(t--){solve();}return 0;
}