基础算法之二分算法 --- 1
大家好,很高兴再次见到各位。接下来我将更新一些较为简单但是很常用的算法,这一部分我将更新有关二分算法的有关内容。
现在就让我们开始对于二分算法的学习吧!
let's go!
前言
大家如果看见前面的基础算法不要觉得就非常简单,可以不用好好学。学习这个部分要有一个认知,基础 ≠ 简单!
基础只是说明了这个算法的使用范围比较广,是我们学习其他算法的一个基础。但是不代表它的题很简单。
一、二分算法初识
我们首先从一道题目来引出二分算法:
题目如下:
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)

题目给出一个非递减排列的数组,让我们在其中找到目标值target的开始位置和结束位置。
还要求时间复杂度到达O(log N)
数组是有序的,我们可以通过target将数组分为两部分
当我们的解具有二段性的时候,就可以使用二分算法来解决
根据待查找的区间中点位置,分析答案出现在哪一侧,接下来舍弃一半,去可能出现答案的另一半查找
下面就是这道题的一个代码:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if (nums.size() == 0) return {-1, -1};int left = 0, right = nums.size() - 1;//左端点while(left < right){int mid = (left + right) / 2;if (nums[mid] >= target) right = mid;else left = mid + 1;}if (nums[left] != target){return {-1, -1};}int retleft = left;left = 0, right = nums.size() - 1;//右端点while (left < right){int mid = (left + right + 1) / 2;if (nums[mid] > target) right = mid - 1;else left = mid;}return {retleft, left};}
};二分模版
在二分算法这里,网上有着很多的模版,博主在这里有两个模版:
//⼆分查找区间左端点
int l = 1, r = n;
while(l < r)
{int mid = (l + r) / 2;if(check(mid)) r = mid;else l = mid + 1;
}//⼆分结束之后可能需要判断是否存在结果
//⼆分查找区间右端点
int l = 1, r = n;
while(l < r)
{int mid = (l + r + 1) / 2;if(check(mid)) l = mid;else r = mid - 1;
}//⼆分结束之后可能需要判断是否存在结果
这个模版在mid位置是否加1是很重要的,关于是否加1可以通过下面的if else中有没有-1
如果下面有-1那么就写+1
模版这里并不是很重要,我们重要的是去理解它
通过前面那道题我们理解一下:
我们要查找这个数,我们就通过二分去查找,如果需要是起始位置的那个数,我们就要让最后left和right相交的位置抵达那里。
就使用了+1的那个模版,因为这样如果nums[mid]大于等于目标值的都被right去当做查找区间的右端点。当nums[mid]小于目标值的时候,left永远向后走,这样就会导致left遇见那个目标值后就不会往后了,这样right和left相遇就是左端点。
同理:找右端点那个也是如此。
时间复杂度
每次二分都会去掉一半的查找区间,时间复杂度为:O(log N)
模版记忆方式
1.不要死记硬背,将算法原理搞清楚,根据题目自然可以写出对应的
2.仅需记住一点,if/else中出现中出现-1 的时候,求mid的时候+1就够了。
STL中的二分查找
头文件:<algorithm>
1.lower_bound:大于等于x的最小元素,返回的是迭代器。时间复杂度:O(log N)
2.upper_bound:大于x的最小元素,返回的是迭代器。时间复杂度:O(log N)
这个STL的二分查找局限性比较大,后面讲的二分答案就不能使用了,因此还是要好好学习二分算法的模版。
二、题目介绍
接下来的这三道题目大家可以自己去尝试解决一下
当学习完这三道题后,大家就会对于二分算法理解起来更加清晰!
牛可乐和魔法封印
P1102 A-B 数对 - 洛谷
P1678 烦恼的高考志愿 - 洛谷
三、牛可乐和魔法封印
题目展示:
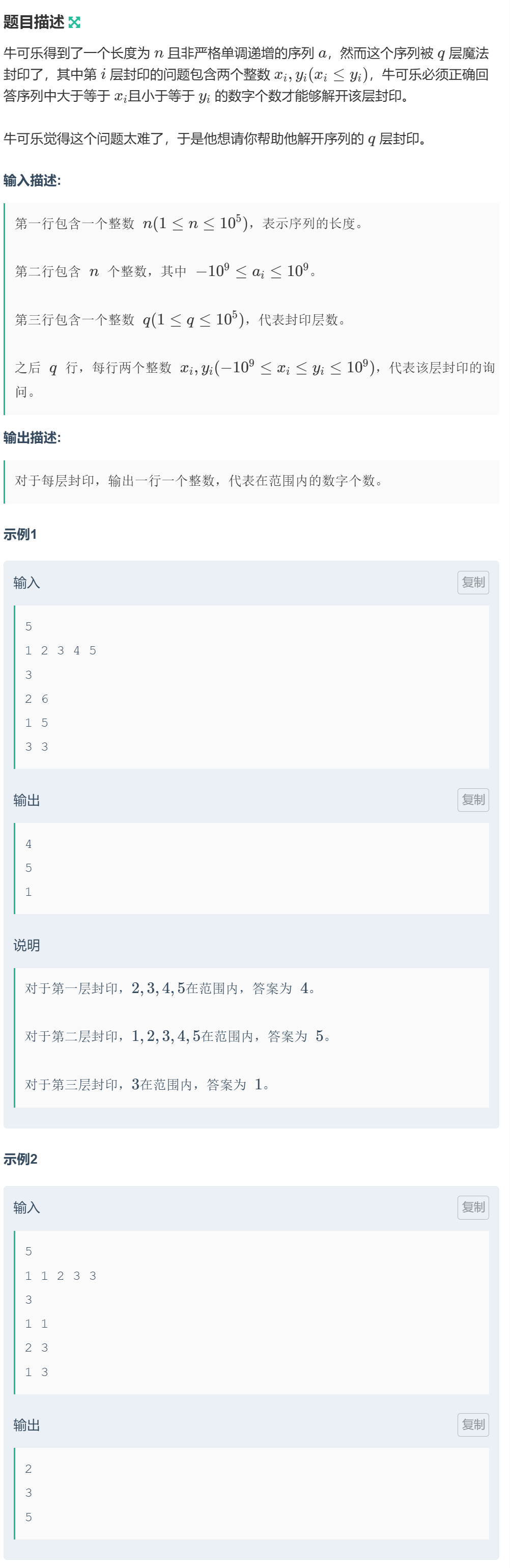
题目分析:
这道题在一个有序数列中查找两个数范围中数的个数,这是和前面那道题很相似的。
我们思路就是通过二分查找到对应的一个下标位置,然后通过下标位置来计算出来在中间的数字的个数。
找到xi数的起始位置和yi的终止位置然后通过减法就可以拿到答案了
还有要注意二分完的最终结果是不是我们想要的答案
代码展示:
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n;
int binary_search(int x, int y)
{//查找x的左端点int l = 1, r = n;while(l < r){int mid = (l + r) / 2;if (a[mid] >= x) r = mid;else l = mid + 1; }//判断查找的结果if (a[l] < x) return 0;//如果没有大于等于x的返回0 int left = l;//查找y的右端点 l = 0, r = n;while(l < r){int mid = (l + r + 1) / 2;if (a[mid] <= y) l = mid;else r = mid - 1;}if (a[l] > y) return 0;//如果没有小于等于y的返回0int right = l;return right - left + 1;
}
int main()
{//输入 cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}int q; cin >> q;while(q--){//q次询问int x, y;cin >> x >> y;cout << binary_search(x, y) << endl;//输出x y中间的数字个数 }return 0;
}
大家会发现这道题和前面的那道题是很相似的,可以好好理解一下,代码难度不大
四、A-B数对
题目展示:
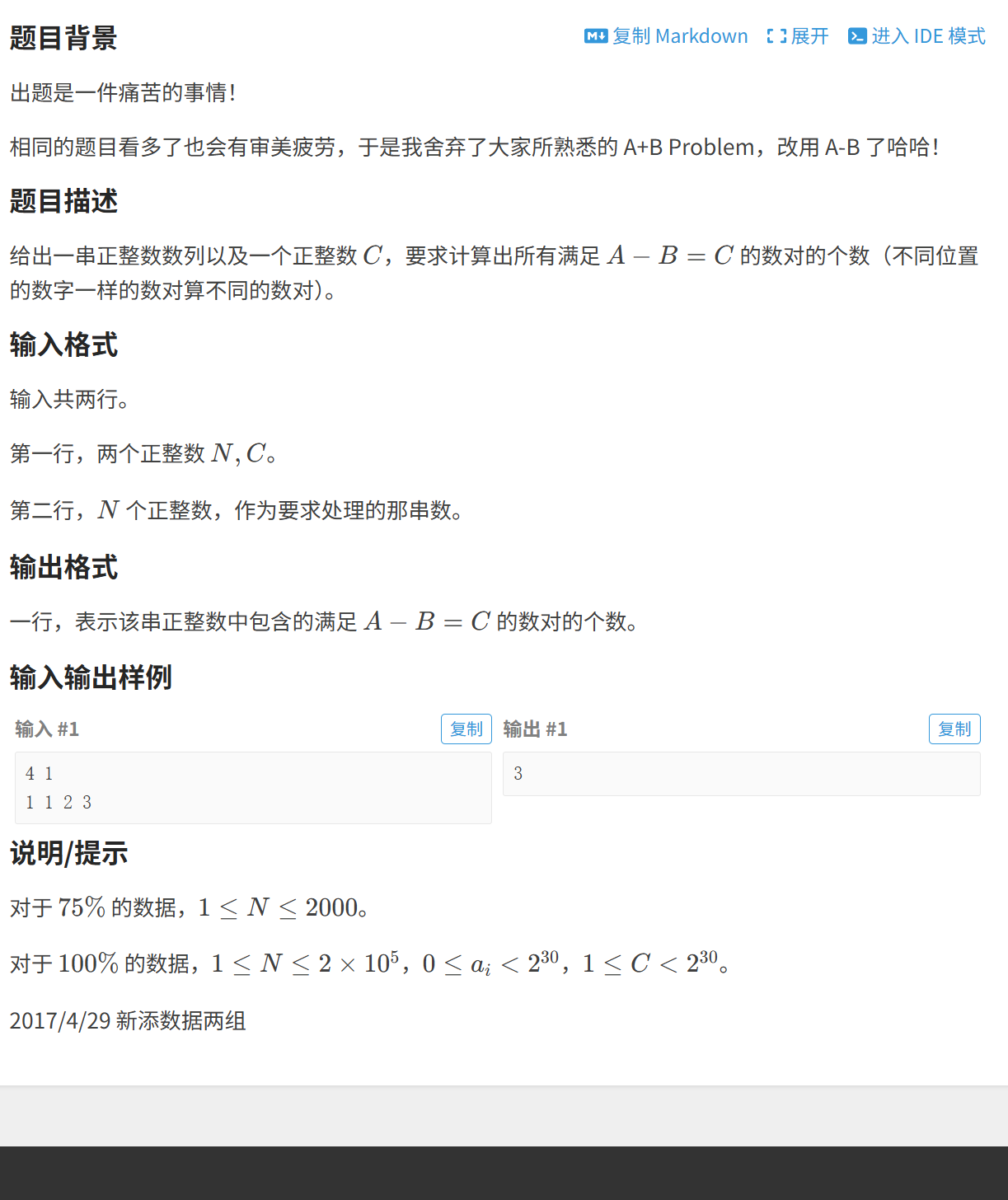
题目分析:
看完题目后,我们可以知道要通过一个C来查找有多少对A、B来满足A - B = C
可以将它理解为B = A - C
枚举数组中的数来作为A,然后在数组中查找为B的数有多少个即可
通过二分查找A有多少个即可了。但是题目没有说它为有序啊?
那可以先将这个数组进行排序,排完序后就可以通过二分来解决了。
其中的数都是大于0的,所以b = a - c > 0 --- a > b
我们查找b的个数都是在1 ~ i里面(i为a的下标)
当然我们还可以将它当做A = B + C来解答
只是,这样相较于前面那种可能要慢点,因为要枚举A的话需要在整个数组来枚举
大家要注意的问题是:数据的大小,数据很大了,避免出现问题,要使用long long 类型来帮助我们!!!
代码展示:
//B = A - C
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int n;
LL a[N];
LL c;
int main()
{cin >> n >> c;for (int i = 1; i <= n; i++) cin >> a[i];sort(a + 1, a + 1 + n);//排成升序LL ret = 0;for (int i = 2; i <= n; i++){LL b = a[i] - c;//b = a - c > 0 --- a > b //查找b的个数,b在1 ~ i里面 ret += upper_bound(a + 1, a + i, b) - lower_bound(a + 1, a + i, b);}cout << ret << endl;return 0;
}//A = B + C
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int n;
LL b[N];
LL c;
int main()
{cin >> n >> c;for (int i = 1; i <= n; i++) cin >> b[i];sort(b + 1, b + 1 + n);//排成升序LL ret = 0;for (int i = 1; i <= n; i++){LL a = b[i] + c;ret += upper_bound(b+1, b+1+n, a) - lower_bound(b+1, b+1+n, a);}cout << ret << endl;return 0;
}五、烦恼的高考志愿
题目展示:
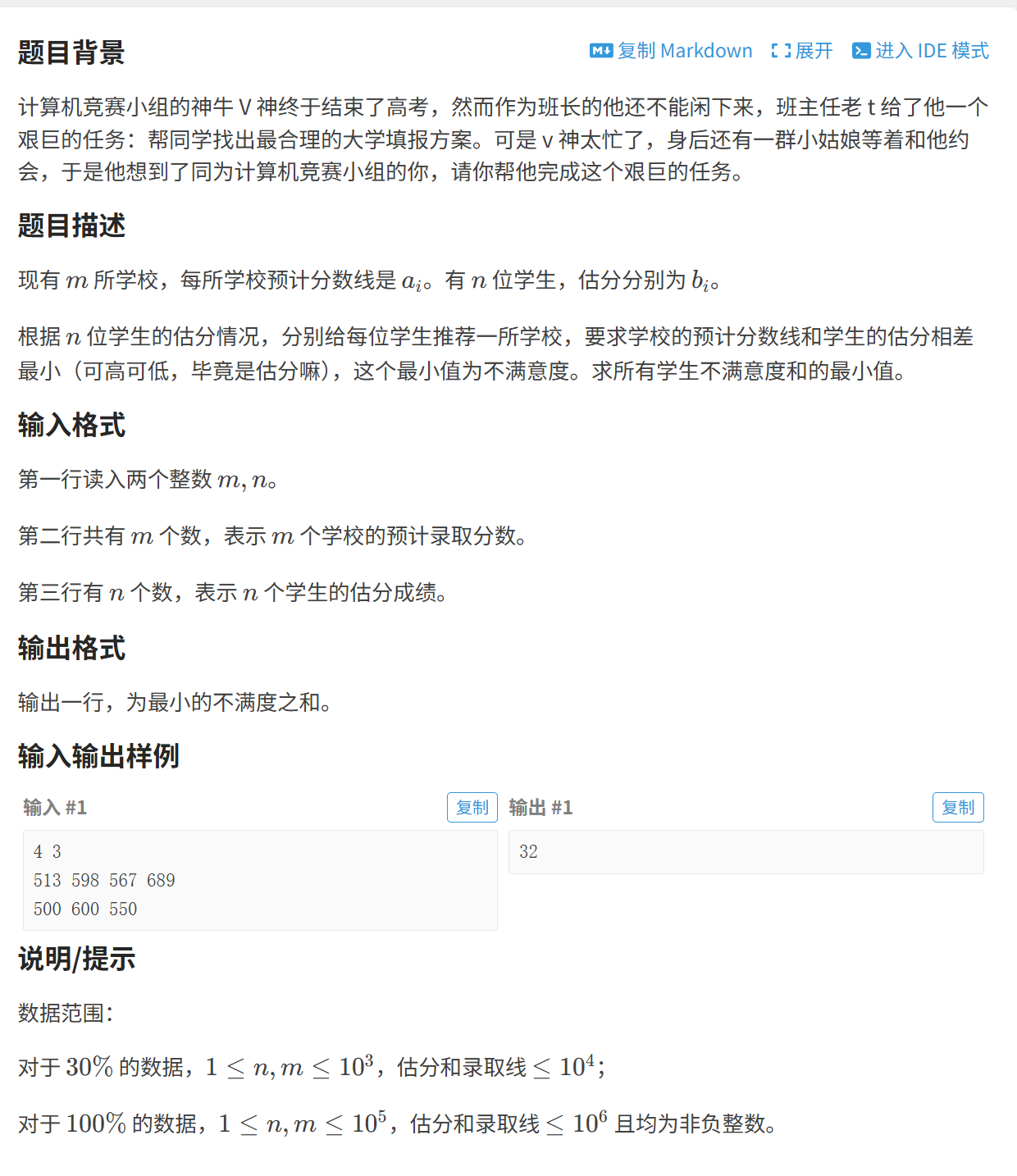
题目分析:
这道题中,我们有着学校的分数和学生的考分,通过学生的考分去找到和学生考分相近的学校分数作为自己的估分,这样估分的不满意度就是最小的了。
那么在这道题中在学校分数中查找和学生分数最相近的学校即可。
那么二分算法就可以使用了
那么就要将学校的分数进行排序,当排成升序后,我们查找大于等于该考生的分数的学校下标pos
就可以通过pos - 1找到小于该考生分数的最大分数的学校
这样,就只需要进行一次二分查找即可
注意下面的ret要使用long long 因为加加之后会超过int的范围
代码展示:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int n, m;
int find(int x)
{int l = 1, r = n;while(l < r){int mid = (l + r) / 2;if (a[mid] >= x) r = mid;else l = mid + 1;}return l;
}
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i];//学校 }sort(a + 1, a + 1 + n);a[0] = -1e7;long long ret = 0;for (int i = 1; i <= m; i++){int b; cin >> b;//学生分数 //查找学校最接近的分数int pos = find(b);ret += min(abs(a[pos] - b), abs(a[pos - 1] - b));}cout << ret <<endl;return 0;
}
结语
希望这篇文章对大家能够有所帮助,后续会更新有关二分答案的内容,可以关注博主。博主持续更新中!
多多点赞 + 收藏 + 关注!!

