当前位置：首页 > backend >正文

对于牛客网—语言学习篇—编程初学者入门训练—复合类型：二维数组较简单题目的解析

backend 2025/9/2 3:29:53

开篇介绍：

本博文秉承着前几篇博客的一贯作风，将对牛客网—语言学习篇—编程初学者入门训练—复合类型：二维数组较简单的题目进行解析，其实这部分题目相对而言，是没有什么含金量的，我感觉就比较适合用来练练手感，但是大家依然也可以去进行作答题目，尤其是对于初学者而言，还是有些许必要性的，所以本篇博客的讲解也会较基础一些，相对而言并没有什么高难度、高技巧、高要求，相信大家一定可以轻松get要点，并顺利解决题目。

这部分还有几道较为困难的题目，我会放在下一篇博客进行讲解，而那其中还有部分较为经典的题目，我会单独开一篇博客进行讲解，大家敬请期待。

下面就先给出这几道较为简单的题目的链接，大家依旧可以在没看解析之前就进行练习，会做最好，不会的话也可以帮助大家更加理解下文的解析。

班级成绩输入输出_牛客题霸_牛客网https://www.nowcoder.com/practice/60d96b08e1cb42e38629d54e37eac008?tpId=290&tqId=618630&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290矩阵元素定位_牛客题霸_牛客网https://www.nowcoder.com/practice/b8e6a46992fe4e11b2822b20561b6d94?tpId=290&tqId=618631&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290最高身高_牛客题霸_牛客网https://www.nowcoder.com/practice/258fe0c567ac493f9b7bc9d3669d158d?tpId=290&tqId=618633&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290矩阵相等判定_牛客题霸_牛客网https://www.nowcoder.com/practice/2f058b1e89ae43f7ab650c0fd0b71fa8?tpId=290&tqId=618634&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290矩阵计算_牛客题霸_牛客网https://www.nowcoder.com/practice/0c83231923c541d2aa15861571831ee5?tpId=290&tqId=320958&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290矩阵转置_牛客题霸_牛客网https://www.nowcoder.com/practice/351b3d03e410496ab5a407b7ca3fd841?tpId=290&tqId=618636&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290序列重组矩阵_牛客题霸_牛客网https://www.nowcoder.com/practice/7548f8f5e44c42fa84fb2323d899a966?tpId=290&tqId=618632&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290图像相似度_牛客题霸_牛客网https://www.nowcoder.com/practice/f2952ee3bb5c48a9be6c261e29dd1092?tpId=290&tqId=309324&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290在进行讲解之前，为防大家可能有些忘记了二维数组，我这边先给大家重温一下二维数组：

二维数组的重温：

在 C 语言中，二维数组本质上是 “数组的数组”，它通过两个维度（行和列）组织数据，适用于存储表格化、矩阵式的数据（如扫雷棋盘、学生成绩表、图像像素矩阵等）。理解二维数组的定义、内存布局、访问方式和使用场景，是掌握 C 语言数据结构的重要基础。

一、二维数组的本质与定义

1. 本质

二维数组并非 “真正的二维结构”，而是一维数组的嵌套—— 即一个一维数组的每个元素，本身又是一个一维数组。例如，int arr[3][4] 可理解为：

外层是一个长度为 3 的一维数组（对应 “行”）；
外层数组的每个元素，是一个长度为 4 的一维数组（对应 “列”）。

2. 定义格式

二维数组的定义需指定数据类型、数组名、两个维度的大小（行大小和列大小），格式如下：

数据类型 数组名[行大小][列大小];

数据类型：数组中所有元素的统一类型（如 int、char、float）；
行大小：二维数组包含的 “外层一维数组” 的个数（即行数）；
列大小：每个 “内层一维数组” 的元素个数（即列数）；
数组元素总数 = 行大小 × 列大小。

示例：

// 定义一个3行4列的int型二维数组（共12个int元素）
int arr1[3][4];// 定义一个5行10列的char型二维数组（共50个char元素，可存5个字符串）
char arr2[5][10];// 定义一个2行2列的float型二维数组（共4个float元素，可存2x2矩阵）
float arr3[2][2];

注意：

C 语言标准规定：二维数组的 “列大小” 必须显式指定，而行大小在某些场景下（如初始化时）可省略（编译器会根据初始化数据自动推导行数）；
数组名是地址常量，指向二维数组的 “首元素”（即第一个内层一维数组的地址），不可被修改（如 arr = &x 是错误的）。

二、二维数组的初始化

二维数组的初始化需遵循 “外层数组元素对应内层数组” 的规则，常用两种方式：按行初始化和按顺序初始化。

1. 按行初始化（推荐）

用大括号 {} 分层包裹每行数据，外层大括号对应 “行”，内层大括号对应 “列”，结构清晰，不易出错。

示例 1：完全初始化（所有元素赋值）

// 3行4列的int数组，每行4个元素
int arr[3][4] = {{1, 2, 3, 4},   // 第0行（索引从0开始）{5, 6, 7, 8},   // 第1行{9, 10, 11, 12} // 第2行
};

示例 2：部分初始化（未赋值元素默认为 0）

若某行元素未完全赋值，剩余元素自动填充为 0；若行数未填满，剩余行也自动填充为 0。

// 第0行赋值3个元素，第4个元素默认为0；第1行赋值2个元素，后2个默认为0；第2行全为0
int arr[3][4] = {{1, 2, 3},      // 第0行：[1,2,3,0]{5, 6},         // 第1行：[5,6,0,0]// 第2行未写，默认为[0,0,0,0]
};

示例 3：省略行大小（编译器自动推导行数）

若初始化时按行赋值，可省略 “行大小”，编译器会根据内层大括号的数量自动计算行数，但列大小必须保留。

// 编译器看到3个内层大括号，自动推导行数为3
int arr[][4] = {{1,2,3,4},{5,6,7,8},{9,10,11,12}
};

2. 按顺序初始化（不推荐）

不区分行，将所有元素按 “行优先” 顺序写在一个大括号内，编译器会按 “先填完一行，再填下一行” 的规则分配元素。
这种方式可读性差，仅适用于简单场景。

示例：

// 等价于按行初始化的{ {1,2,3,4}, {5,6,7,8}, {9,10,11,12} }
int arr[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};// 部分赋值：前5个元素按顺序填充，剩余元素为0
int arr[3][4] = {1,2,3,4,5}; 
// 第0行：[1,2,3,4]，第1行：[5,0,0,0]，第2行：[0,0,0,0]

3. 字符型二维数组的初始化（存多个字符串）

字符型二维数组常用于存储多个字符串（每个内层数组存一个字符串，需预留字符串结束符 '\0' 的位置）。

示例：

// 5行10列的char数组，存5个字符串（每个字符串最长9个字符+1个'\0'）
char strs[5][10] = {"apple",   // 第0行：'a','p','p','l','e','\0',0,0,0,0"banana",  // 第1行：'b','a','n','a','n','a','\0',0,0,0"cherry"   // 第2行：'c','h','e','r','r','y','\0',0,0,0// 第3、4行默认为全0（即空字符串）
};

三、二维数组的内存布局

二维数组在内存中是连续存储的，遵循 “行优先” 原则（即先存储第 0 行的所有元素，再存储第 1 行，以此类推），不存在 “行与行之间的间隔”。

示例：以 `int arr[3][4]` 为例

假设 int 占 4 字节，数组首地址为 0x100，则内存布局如下：

元素	arr[0][0]	arr[0][1]	arr[0][2]	arr[0][3]	arr[1][0]	arr[1][1]	arr[1][2]	arr[1][3]	arr[2][0]	arr[2][1]	arr[2][2]	arr[2][3]
内存地址	0x100	0x104	0x108	0x10C	0x110	0x114	0x118	0x11C	0x120	0x124	0x128	0x12C
存储内容	1	2	3	4	5	6	7	8	9	10	11	12

关键结论：

二维数组的地址计算：arr[i][j] 的地址 = 数组首地址 + (i × 列大小 + j) × 元素字节数；
数组名 arr 等价于 &arr[0]（指向第 0 行的地址，即内层一维数组的地址）；
arr[i] 等价于 &arr[i][0]（指向第 i 行第 0 列元素的地址）。

四、二维数组的元素访问

二维数组的元素通过双重索引访问，格式为 数组名[行索引][列索引]，索引从 0 开始（第 0 行、第 0 列）。

1. 直接访问（`arr[i][j]`）

最常用的方式，通过行索引 i 和列索引 j 直接定位元素，编译器会自动计算元素地址。

示例：遍历并修改二维数组

#include <stdio.h>int main() {int arr[3][4] = {{1,2,3,4},{5,6,7,8},{9,10,11,12}};// 遍历二维数组：外层循环控制行，内层循环控制列for (int i = 0; i < 3; i++) {  // i：行索引（0~2）for (int j = 0; j < 4; j++) {  // j：列索引（0~3）arr[i][j] *= 2;  // 修改元素：每个元素乘以2printf("%d ", arr[i][j]);  // 输出修改后的值}printf("\n");  // 每行结束换行}return 0;
}

输出结果：

2 4 6 8 
10 12 14 16 
18 20 22 24

2. 指针访问（理解内存布局）

由于二维数组在内存中连续存储，也可通过指针间接访问元素（需注意指针类型匹配）。

核心指针关系：

arr：类型为 int (*)[4]（指向 “包含 4 个 int 的数组” 的指针），值为第 0 行的地址；
arr + i：指向第 i 行的地址（偏移 i × 4 × sizeof(int) 字节）；
*(arr + i)：等价于 arr[i]，类型为 int*（指向第 i 行第 0 列元素的指针）；
*(arr + i) + j：指向第 i 行第 j 列元素的地址；
*(*(arr + i) + j)：等价于 arr[i][j]，即第 i 行第 j 列元素的值。

示例：用指针遍历数组

#include <stdio.h>int main() {int arr[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};// 指针p指向第0行（类型匹配：int (*)[4]）int (*p)[4] = arr;for (int i = 0; i < 3; i++) {// 指针q指向第i行第0列元素（类型匹配：int*）int *q = *(p + i);for (int j = 0; j < 4; j++) {printf("%d ", *(q + j));  // 等价于 arr[i][j]}printf("\n");}return 0;
}

五、二维数组作为函数参数

在 C 语言中，二维数组作为函数参数时，必须显式指定列大小（因为编译器需要通过列大小计算元素地址），行大小可省略。

1. 正确的参数传递方式

方式 1：指定列大小（推荐）

// 形参：arr[][4]（列大小4必须保留，行大小可省略）
void printArr(int arr[][4], int rows) {for (int i = 0; i < rows; i++) {for (int j = 0; j < 4; j++) {printf("%d ", arr[i][j]);}printf("\n");}
}int main() {int arr[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};printArr(arr, 3);  // 实参：数组名arr（指向第0行的地址）、行数3return 0;
}

方式 2：用指针表示（等价于方式 1）

由于 arr[][4] 本质是 “指向包含 4 个 int 的数组的指针”，可直接用指针类型 int (*arr)[4] 作为形参，效果完全相同：

// 形参：int (*arr)[4]（与arr[][4]等价）
void printArr(int (*arr)[4], int rows) {// 函数体与方式1完全一致
}

2. 错误的参数传递方式

错误 1：省略列大小（编译器无法计算元素地址）
void printArr(int arr[][], int rows, int cols) → 编译报错；
错误 2：用一级指针接收（类型不匹配）
void printArr(int *arr, int rows, int cols) → 若传入 arr（类型为 int (*)[4]），会导致类型不兼容。

六、二维数组的常见应用场景

矩阵运算：如矩阵加法、乘法、转置（需存储行和列的元素）；
示例：2x2 矩阵加法

int mat1[2][2] = {{1,2},{3,4}}, mat2[2][2] = {{5,6},{7,8}}, res[2][2];
for (int i=0; i<2; i++)for (int j=0; j<2; j++)res[i][j] = mat1[i][j] + mat2[i][j];

表格数据存储：如学生成绩表（行：学生，列：科目成绩）；

// 3个学生，2门科目（语文、数学）
int scores[3][2] = {{90, 85}, {88, 92}, {76, 80}};

字符矩阵 / 多字符串存储：如扫雷棋盘（* 表示地雷，. 表示空白）、文本编辑器的多行文本；

// 5x5扫雷棋盘
char mineMap[5][5] = {{'*', '.', '.', '*', '.'},{'.', '.', '*', '.', '.'},{'.', '*', '.', '.', '*'}
};

七、注意事项

数组越界问题：访问时行索引需小于行大小，列索引需小于列大小（如 arr[3][4] 访问 arr[3][0] 会越界），越界访问会破坏其他内存数据，导致程序崩溃；
列大小不可省略：定义二维数组或作为函数参数时，列大小必须显式指定（除非初始化时按行赋值且省略行大小）；
内存连续存储：二维数组的连续性可用于 “一维数组模拟二维数组”（通过公式 i × cols + j 计算索引），适用于列大小动态变化的场景。

BC128 班级成绩输入输出：

本题难度相当于没有，考验大家对二维数组的基本概念，我们看题目：

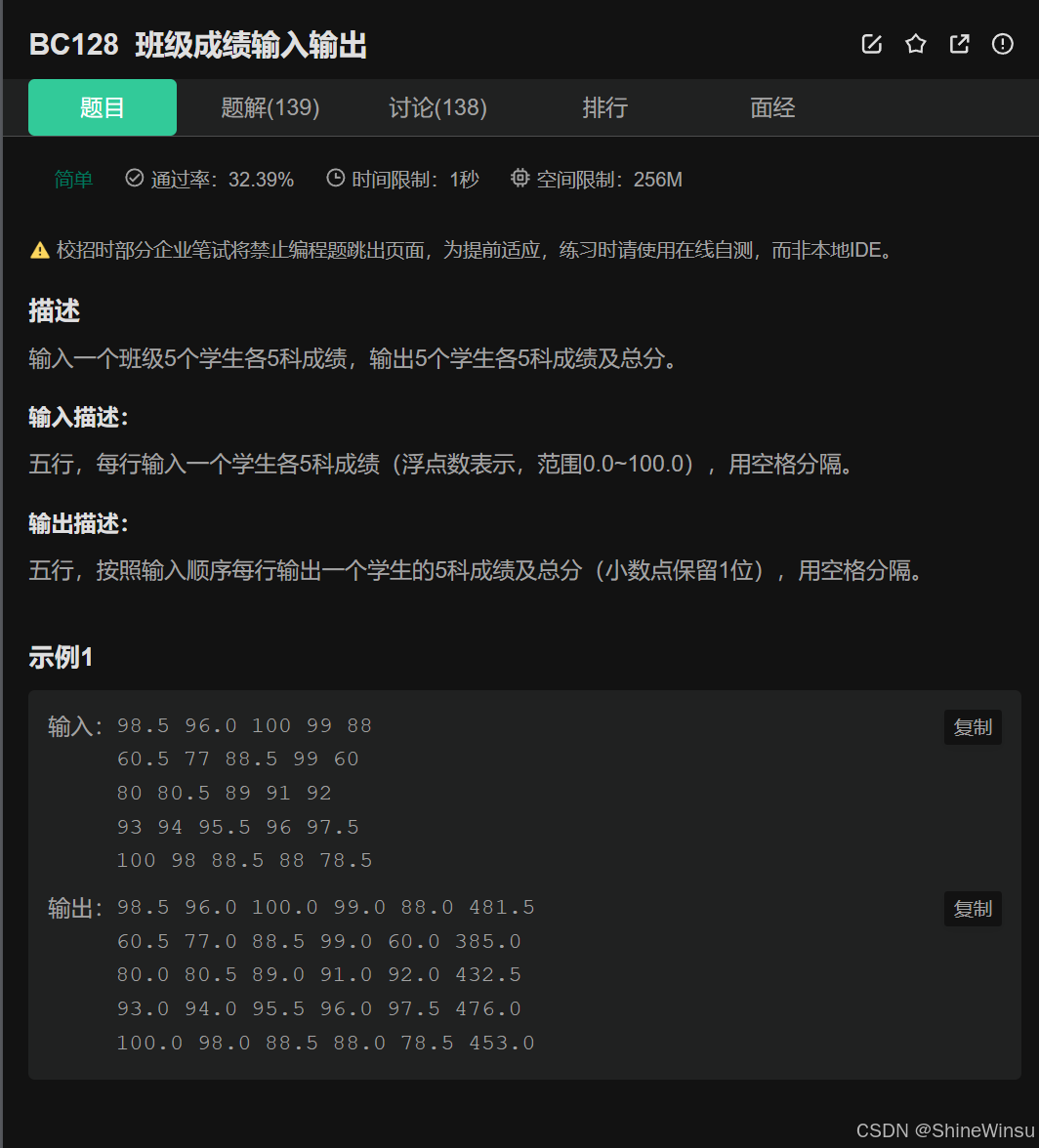
我们先来分析一下题意：

题意分析：

该题要求处理班级学生的成绩输入输出，核心要点如下：

输入部分

需读取 5 组数据，每组对应 1 个学生的 5 科成绩（浮点数，范围 0.0~100.0）。
输入形式为 5 行，每行有 5 个浮点数，以空格分隔。

输出部分

需输出 5 行，每行对应 1 个学生的成绩结果。
每行包含 6 个浮点数：前 5 个是该学生的 5 科成绩（需保留 1 位小数），最后 1 个是该学生 5 科成绩的总分（也需保留 1 位小数）。
所有数之间以空格分隔，输出顺序与输入学生的顺序一致。

处理逻辑

对每个学生的 5 科成绩，既要格式化输出（保留 1 位小数），又要计算它们的总和（作为总分）。
注意浮点数的精度处理，确保总分计算和小数格式化符合要求。

解答题目：

知道了题目想要表达的意思之后，相信大家对这道题也是手拿把掐了，这道题唯一算是难的一个点大概就是要求在输出完每一个学生的5科成绩后输出5科成绩的总和，所以这也就意味着原数组每一行的总和，并进行输出，那么这一步我们要怎么实现呢？

其实并不难，我们可以设置一个变量sum去接收一行的数据之和，然后在表达完一行之后，就把这个变量表达出，但是这里大家可能有个问题，那这个sum在接收完第一行的数据之和之后，它再接收第二行的数据之和，不是会变成两行的数据之和了吗，诶，既然不想让sum即既存储第一行又存储第二行，那我们就在sum接收完第一行总和之后，让它变为0，这样子不就抛去了第一行的数据之和，可以正常知道第二行的数据之和，后面几行的操作也是类似。

这一个操作其实前几篇博客就有提及过，大家如果想要更加的深入了解这一操作，可以看看前面几篇博客。

下面是想要解决本题需要的几步，大家可以看看自己的思路会不会更好：

第一步是准备数据存储区域，创建一个合适的结构来存放 5 名学生的每科成绩，确保能容纳 5 行（对应 5 名学生）、每行 5 个（对应 5 科）的成绩数据，并初始化为默认状态。

第二步是获取输入数据，通过逐行逐科的方式读取成绩。具体来说，依次处理每一名学生，对每名学生依次读取 5 科成绩，将这些成绩按照学生和科目的对应关系，存放到之前准备的存储结构中。

第三步是处理并输出每个学生的成绩及总分。对每一名学生，先准备一个用于累加总分的变量（即sum）并初始化为 0；然后依次取出该学生的 5 科成绩，每取出一科成绩就立即按保留 1 位小数的格式输出，同时将这科成绩累加到总分变量中；当 5 科成绩都输出完成后，再将累加得到的总分按保留 1 位小数的格式输出在这行的末尾。

第四步是重置与换行，在完成一名学生的成绩处理和输出后，将用于累加总分的变量重置为 0，以确保计算下一名学生的总分时不受之前数据的影响，同时进行换行操作，为下一名学生的成绩输出做好格式准备。

下面是本题的完整解题代码：

#include <stdio.h>int main()
{float arr[5][5] = { 0 };for (int i = 0; i < 5; i++){for (int j = 0; j < 5; j++){scanf("%f",&arr[i][j]);}}float sum = 0;for (int i = 0; i < 5; i++){for (int j = 0; j < 5; j++){sum = sum + arr[i][j];printf("%.1f ",arr[i][j]);}printf("%.1f",sum);sum = 0;//进行完一行相加后就清0printf("\n");//换行}return 0;
}

由于题目比较简单，所以我就不提供详细注释了，相信大家一定可以看懂，如果依然不懂，可以再去仔细研究一下那几个步骤。

BC129 矩阵元素定位：

这道题也不难，不过需要我们勘破题目所给的一个与我们平时固定思维相悖的陷阱，我们依然是先看题目：

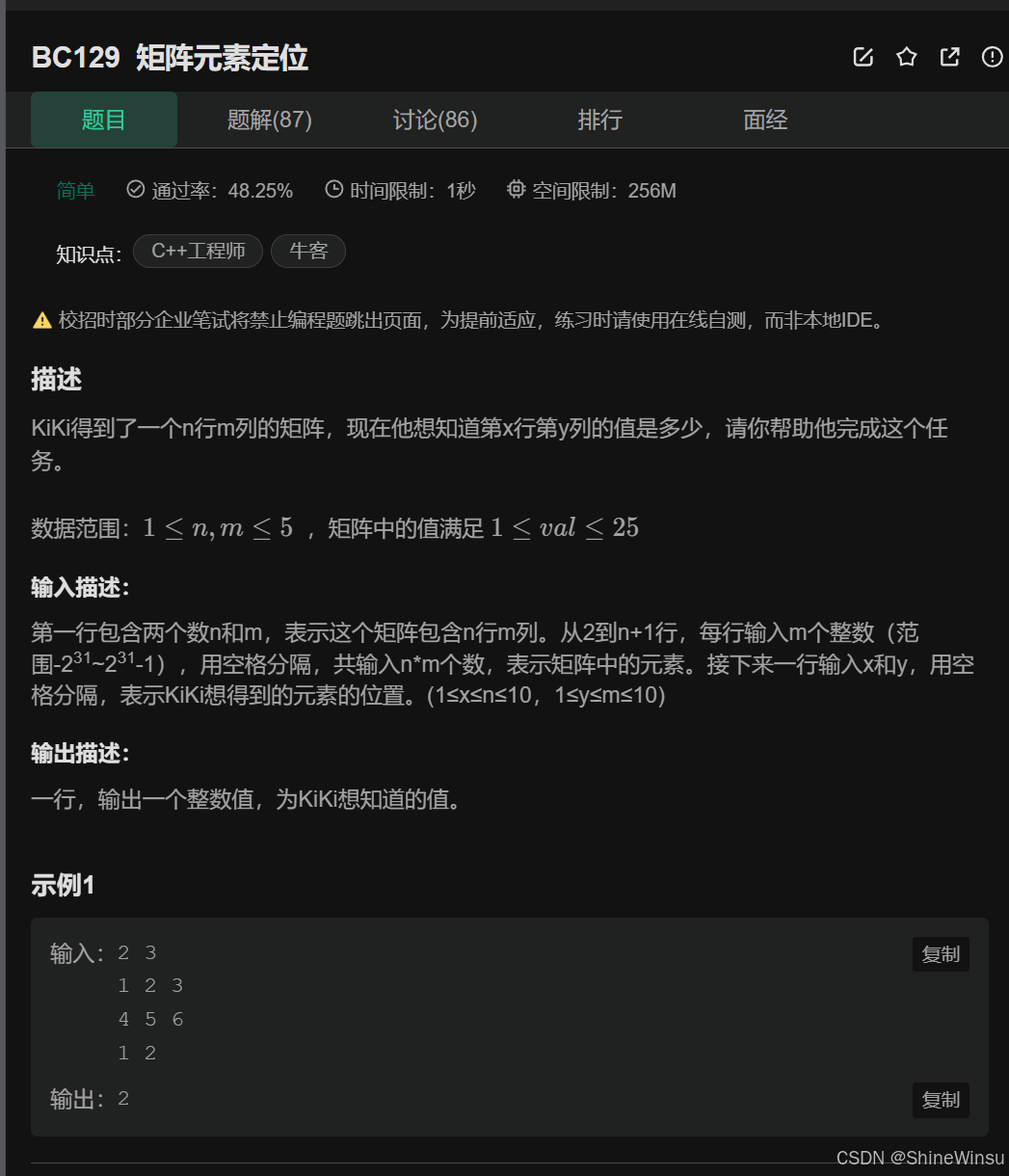
题意分析：

1. 输入分析

输入分为三个部分：

第一部分：一行两个整数 n 和 m，表示矩阵的行数（n 行）和列数（m 列）。
第二部分：接下来的 n 行，每行有 m 个整数，是矩阵的具体元素（共 n×m 个元素）。
第三部分：最后一行两个整数 x 和 y，表示要查询的目标位置（第 x 行、第 y 列）。

2. 输出

输出：一行，输出目标位置的整数值。

陷阱排查：

其实光看这道题目，是不难的，大家都会的操作，先创建二维数组并接收数据，之后再去输出题目要求定位的arr[x][y]。

但是真的有这么简单吗？很显然，不可能，那么陷阱是什么呢？且看下文：

这道题的核心陷阱在于 “行、列的计数方式不匹配”，具体来说：

1. 题目里的 “行、列” 是「1 开始计数」

比如题目说 “第 1 行第 2 列”，是按照人类的习惯 ——“第几个” 来数的（从 1 开始）。

2. 编程语言中数组的「索引是 0 开始计数」

在 C 语言（或大多数语言）里，数组的第一行对应的索引是0，第二行是1……；第一列索引是0，第二列是1……。

3. 直接用题目输入的 “x、y” 会出错

如果题目输入要查 “第 x 行第 y 列”，你直接写 arr[x][y] 去访问数组，就会取错位置。

比如：
假设矩阵是：
1 2 3
4 5 6
题目要查 “第 1 行第 2 列”（正确值是2）。如果直接用 arr[1][2]，实际访问的是第二行第三列（值为6），结果就错了。

所以，我们就得知道这一个坑，并去精确避开，只不过要用什么方法呢？

我这边提供两个方法，大家可以根据个人喜好进行选择：

方法一：1.输入后直接转换索引

当从输入中读取到要查询的 “第 x 行第 y 列” 后，立即把 x 和 y 都减 1，将其转换为数组的 0 开始索引。
比如（以 C 语言为例）：

int x, y;
scanf("%d %d", &x, &y);
x--;  // 行从1→0
y--;  // 列从1→0
// 之后直接用arr[x][y]访问数组

方法一：2.访问时实时转换索引

读取 x 和 y 后不修改它们，在访问数组的瞬间，用 x-1 和 y-1 作为索引。
比如（以 C 语言为例）：

int x, y;
scanf("%d %d", &x, &y);
// 访问时用x-1、y-1，直接转换
int target = arr[x-1][y-1];

方法二：在输入的时候忽略对0行0列的输入，直接从1行1列开始输入

这种方法的核心是 “用空间换便捷”，通过调整数组的使用方式，让输入 / 查询的 “行、列编号” 直接匹配题目里 “从 1 开始计数” 的规则，具体逻辑是：

1. 数组索引的特殊利用

C 语言数组默认从 0 开始索引（如 arr[0][0] 是 “第 0 行第 0 列”），但此方法会故意闲置数组的 “第 0 行” 和 “第 0 列”，不往这些位置存数据。

2. 输入时的操作

输入矩阵数据时，直接从 “第 1 行第 1 列” 开始填充（对应数组的 arr[1][1]）。例如：

题目中 “第 1 行” 的数据，存在数组的 arr[1][1]、arr[1][2]...；
题目中 “第 2 行” 的数据，存在数组的 arr[2][1]、arr[2][2]...；
数组的 arr[0][...]、arr[...][0] 这些 “0 开头” 的位置，完全闲置（不存有效数据）。

3. 查询时的便利

当题目要查 “第 x 行第 y 列” 时，直接用 arr[x][y] 访问即可，无需把 x、y 减 1 转换成 “0 开始的索引”—— 因为输入时就已经把 “第 1 行” 对应到 arr[1]，“第 1 列” 对应到 arr[...][1] 了。

优缺点

优点：输入和查询时，行、列编号能直接和题目描述的 “第 x 行第 y 列” 对应，不用手动做 “减 1” 的转换，逻辑更直观。
缺点：浪费了数组 “第 0 行” 和 “第 0 列” 的存储空间（如果矩阵规模很大，浪费会更明显，但题目通常限制矩阵规模小，所以影响不大）。

简单说，就是通过 “空出数组前 0 行 0 列”，让后续的行、列编号和题目保持一致，省去索引转换的步骤。

即如下代码：

	for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d",&arr[i][j]);}}

这两种方法各有千秋，大家可以自由选择，不过在需要矩阵规模较大时，我个人比较推荐使用方法一，而若是在一些规模较小，需要快速解决的情况下，第二种方法可能就会更加适合。

继续解答：

在知道了这道题的小陷阱之后，这道题就毫无难度可言了，下面直接给出完整代码：

#include <stdio.h>int main()
{int n, m;scanf("%d%d",&n,&m);int arr[100][100] = { 0 };for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d",&arr[i][j]);}}int x, y;scanf("%d%d",&x,&y);printf("%d",arr[x][y]);return 0;
}

由于题目比较简单，所以我依然就不提供详细注释了，相信大家一定可以看懂，如果依然不懂，可以再去仔细研究一下上文。

BC130 最高身高：

我们直接看题目：

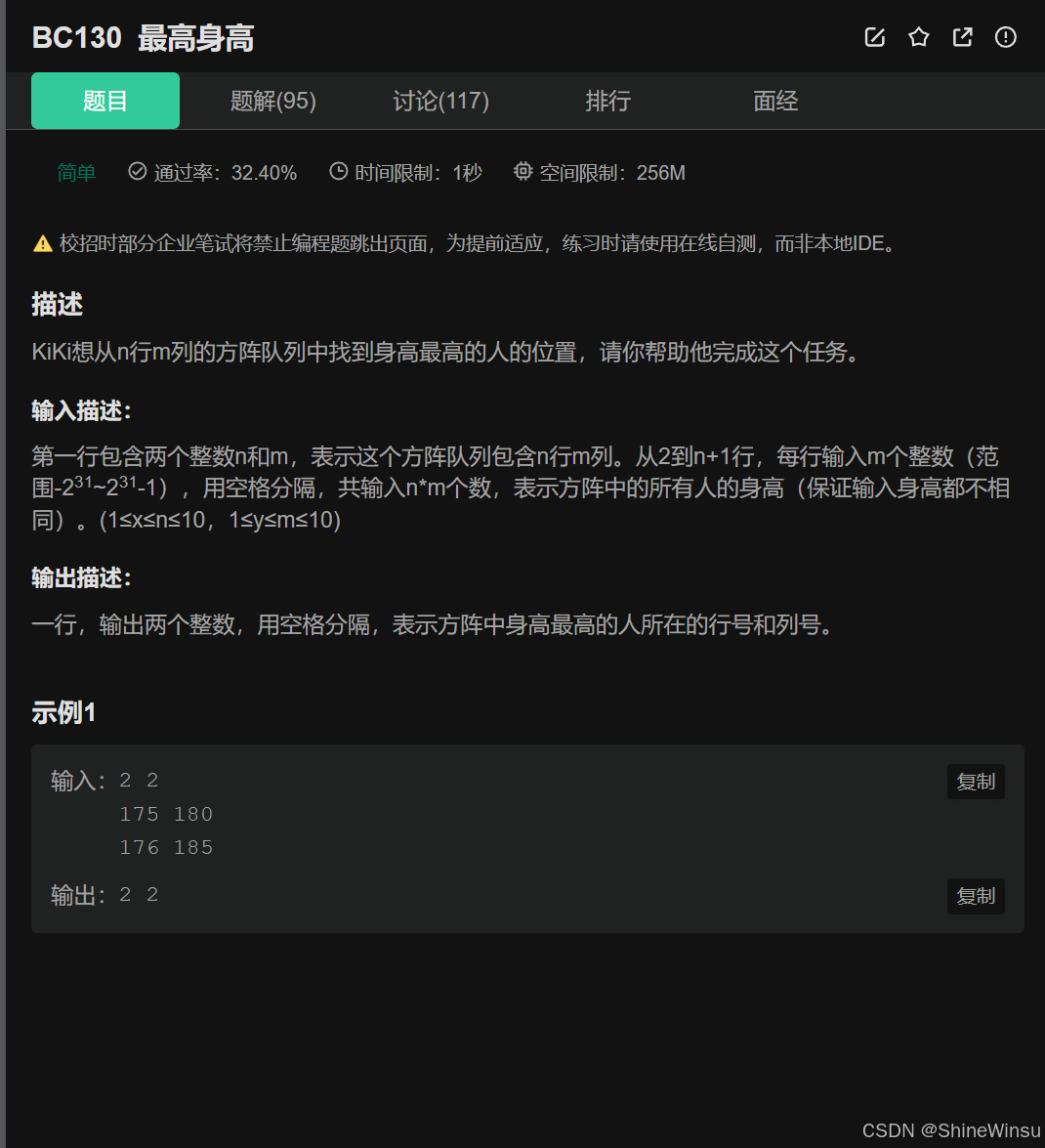
题意分析：

这道题的题意可分为输入、处理要求、输出三个部分来分析：

输入部分

第一行输入两个整数 n 和 m，表示方阵有 n 行、m 列。
接下来输入 n 行数据，每行有 m 个整数，代表方阵中每个人的身高（所有身高均不重复）。

处理要求

在 n 行 m 列的方阵中，找到身高最高的人，并确定其所在的行号和列号。

输出部分

输出一行，包含两个整数（用空格分隔），分别是最高身高的人所在的行号和列号（行号、列号从 1 开始计数，例如 “第 2 行第 2 列” 输出为 2 2）。

关键细节

所有身高互不相同，因此 “最高身高” 是唯一的。

相信聪明的大家经过上一题的陷阱，肯定能够发现本题也有着这一个小陷阱，其实以后大家想要判定类似的题目有没有这一个陷阱时，大家可以直接对题目所给的例子进行坐标分析，看看按照题目所要求的行列，是否符合平时按0开始存储的行列，

以本题示例分析：

输入示例中，方阵是 2 行 2 列：

第 1 行数据：175、180；
第 2 行数据：176、185。

最高身高是 185，它在第 2 行第 2 列，输出也是 2 2。

若按 “数组 0 开始存储” 的习惯：

第 1 行数据会存在数组的 arr[0][0]（175）、arr[0][1]（180）；
第 2 行数据会存在数组的 arr[1][0]（176）、arr[1][1]（185）。

此时最高身高 185 在数组中是 第 1 行（0 开始）、第 1 列（0 开始），但题目输出是 2 2。这说明：题目要求的 “行号、列号是从 1 开始计数”，而非数组默认的 “0 开始索引”。

继续解答：

知道了题意之后，我们就可以开始思考这道题需要怎么解决了，其实并不难，只需要下面这几步就行了：

步骤 1：读取矩阵的行数和列数

输入两个整数 n 和 m，分别表示矩阵的行数和列数（例如输入 2 2，表示 2 行 2 列的矩阵）。
定义一个二维数组 arr[100][100] 用于存储矩阵元素，初始化为 0。

步骤 2：按 “1 开始索引” 存储矩阵元素

使用嵌套循环读取矩阵元素：外层循环变量 i 从 1 遍历到 n（对应题目中的 “第 1 行到第 n 行”），内层循环变量 j 从 1 遍历到 m（对应题目中的 “第 1 列到第 m 列”）。
将读取到的每个元素直接存入 arr[i][j]（例如第 1 行第 2 列的元素存到 arr[1][2]），此时数组的 arr[0][...] 和 arr[...][0] 位置闲置（不存储有效数据）。

步骤 3：遍历矩阵找到最大值

初始化变量 max 为 0，用于记录最高身高。
再次通过嵌套循环遍历矩阵：i 从 1 到 n，j 从 1 到 m，逐个比较 arr[i][j] 与 max。
若 arr[i][j] 大于当前 max，则更新 max 为该元素值，最终 max 即为矩阵中的最高身高。

步骤 4：定位最大值所在的行号和列号

定义变量 n1 和 m1，用于存储最高身高所在的行号和列号。
第三次通过嵌套循环遍历矩阵：i 从 1 到 n，j 从 1 到 m，当找到 arr[i][j] 等于 max 时，将当前的 i（行号）和 j（列号）分别赋值给 n1 和 m1，并跳出内层循环（因最大值唯一，无需继续查找）。

步骤 5：输出结果

直接打印 n1 和 m1，这两个值就是题目要求的 “从 1 开始计数” 的行号和列号（例如找到最大值在 arr[2][2]，则输出 2 2）。

由此，本题依旧是轻轻松松，下面给出完整代码：

#include <stdio.h>int main()
{int n, m;scanf("%d%d", &n, &m);int arr[100][100] = { 0 };for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &arr[i][j]);}}int max = 0;//直接遍历找最大值for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (arr[i][j] > max){max = arr[i][j];}}}int n1, m1;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (max == arr[i][j]){n1 = i;m1 = j;break;}}}printf("%d %d",n1,m1);
}

由于题目比较简单，所以我依然就不提供详细注释了，相信大家一定可以看懂，如果依然不懂，可以再去仔细研究一下上文。

BC131 矩阵相等判定：

这道题老样子，较为简单，我们看题目：

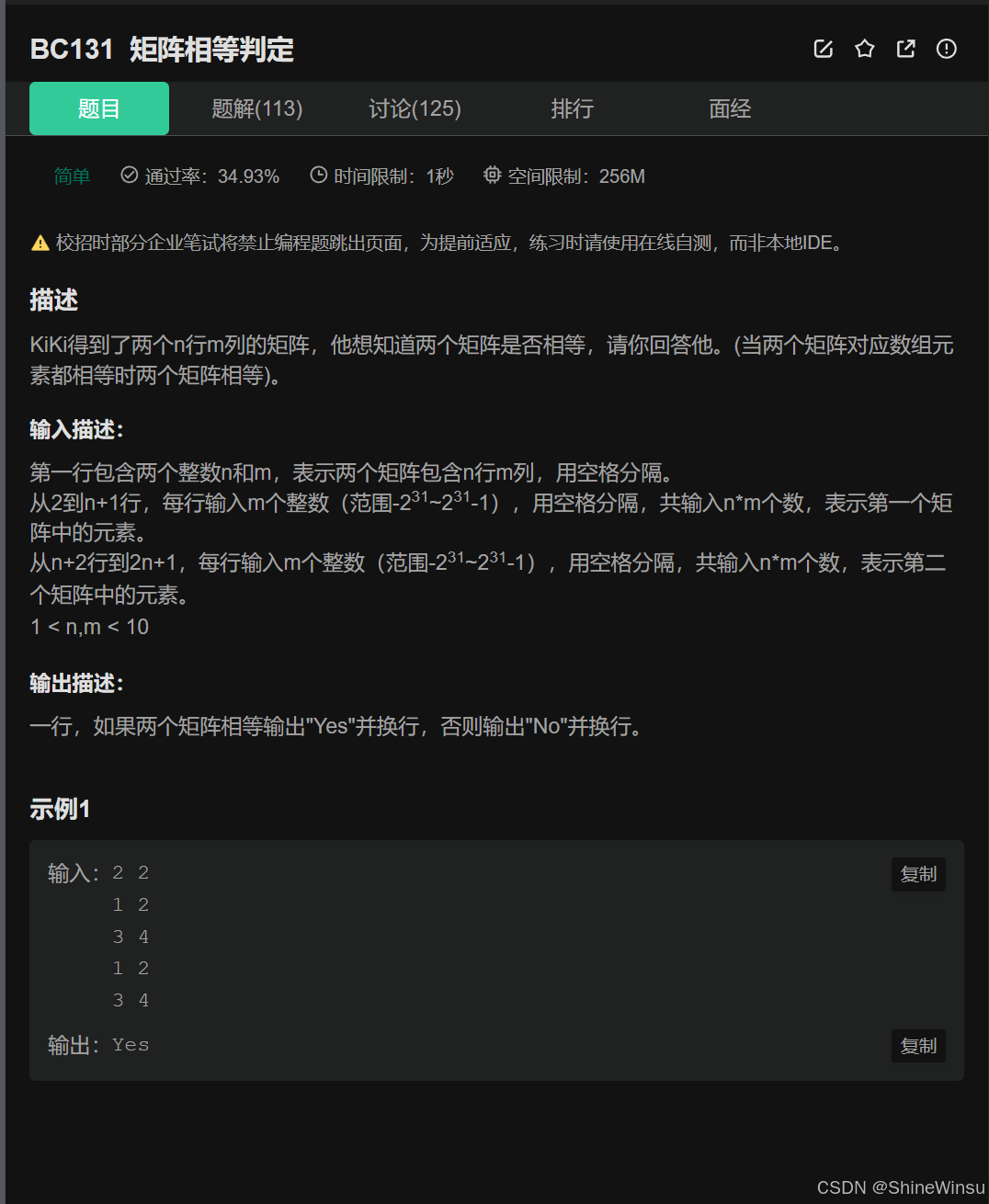
题意分析：

任务目标

判断两个 n行m列 的矩阵是否相等（当且仅当两个矩阵对应位置的所有元素都完全相同时，矩阵相等）。

输入规则

第一行输入两个整数 n 和 m，表示两个矩阵的行数和列数（两个矩阵规模相同）。
接下来 n 行：输入第一个矩阵的元素，每行 m 个整数。
再接下来 n 行：输入第二个矩阵的元素，每行 m 个整数。

输出规则

若两个矩阵对应位置的元素全部相等，输出 "Yes" 并换行；
若存在任意一个位置的元素不相等，输出 "No" 并换行。

这道题就没有上面两道题的陷阱了，毕竟它没有进行某个元素的查找或者位置坐标输出。

那么我们就开始解答本题：

步骤 1：读取矩阵规模并初始化存储结构

输入两个整数 n 和 m，分别表示两个矩阵的行数和列数（例如输入 2 3，表示两个矩阵均为 2 行 3 列）。
定义两个二维数组 arr1[100][100] 和 arr2[100][100]，用于分别存储两个矩阵的元素，初始化为 0。

步骤 2：读取并存储第一个矩阵的元素

使用嵌套循环读取第一个矩阵的元素：外层循环变量 i 从 1 遍历到 n（对应 “第 1 行到第 n 行”），内层循环变量 j 从 1 遍历到 m（对应 “第 1 列到第 m 列”）。
将读取到的元素存入 arr1[i][j]（例如第 2 行第 3 列的元素存到 arr1[2][3]），数组的 arr1[0][...] 和 arr1[...][0] 位置闲置。

步骤 3：读取并存储第二个矩阵的元素

用与步骤 2 完全相同的方式，读取第二个矩阵的元素：i 从 1 到 n，j 从 1 到 m，将元素存入 arr2[i][j]（例如第 1 行第 1 列的元素存到 arr2[1][1]）。

步骤 4：逐元素比较两个矩阵

定义标记变量 flag 并初始化为 1（1 表示 “矩阵相等”，0 表示 “不相等”）。这一步和判断素数非常类似，大家有不懂的可以看这一篇博客：对于判断素数（质数）以及牛客网—语言学习篇—编程初学者入门训练—复合类型：字符/字符数组的题目解析-CSDN博客
遍历两个矩阵的所有对应（相对应的行与列）位置：i 从 1 到 n，j 从 1 到 m，逐个比较 arr1[i][j] 与 arr2[i][j]。
若发现任意一对对应元素不相等（arr1[i][j] != arr2[i][j]），则将 flag 设为 0，并跳出当前内层循环（无需继续比较后续元素）。

步骤 5：根据比较结果输出结论

若 flag 仍为 1（所有对应元素均相等），输出 "Yes"；
若 flag 变为 0（存在不相等的元素），输出 "No"。

由此，本题依旧毫无压力的结束了，下面是完整代码：

#include <stdio.h>int main()
{int n, m;scanf("%d%d", &n, &m);int arr1[100][100] = { 0 };int arr2[100][100] = { 0 };for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &arr1[i][j]);}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &arr2[i][j]);}}int flag = 1;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (arr1[i][j] != arr2[i][j]){flag = 0;break;}}}if (flag == 1){printf("Yes");}else{printf("No");}return 0;
}

由于题目比较简单，所以我依然就不提供详细注释了，相信大家一定可以看懂，如果依然不懂，可以再去仔细研究一下上文。

BC132 矩阵计算：

这道题可以说是比上面几题还要简单，我们看题目：

题意分析：

核心任务

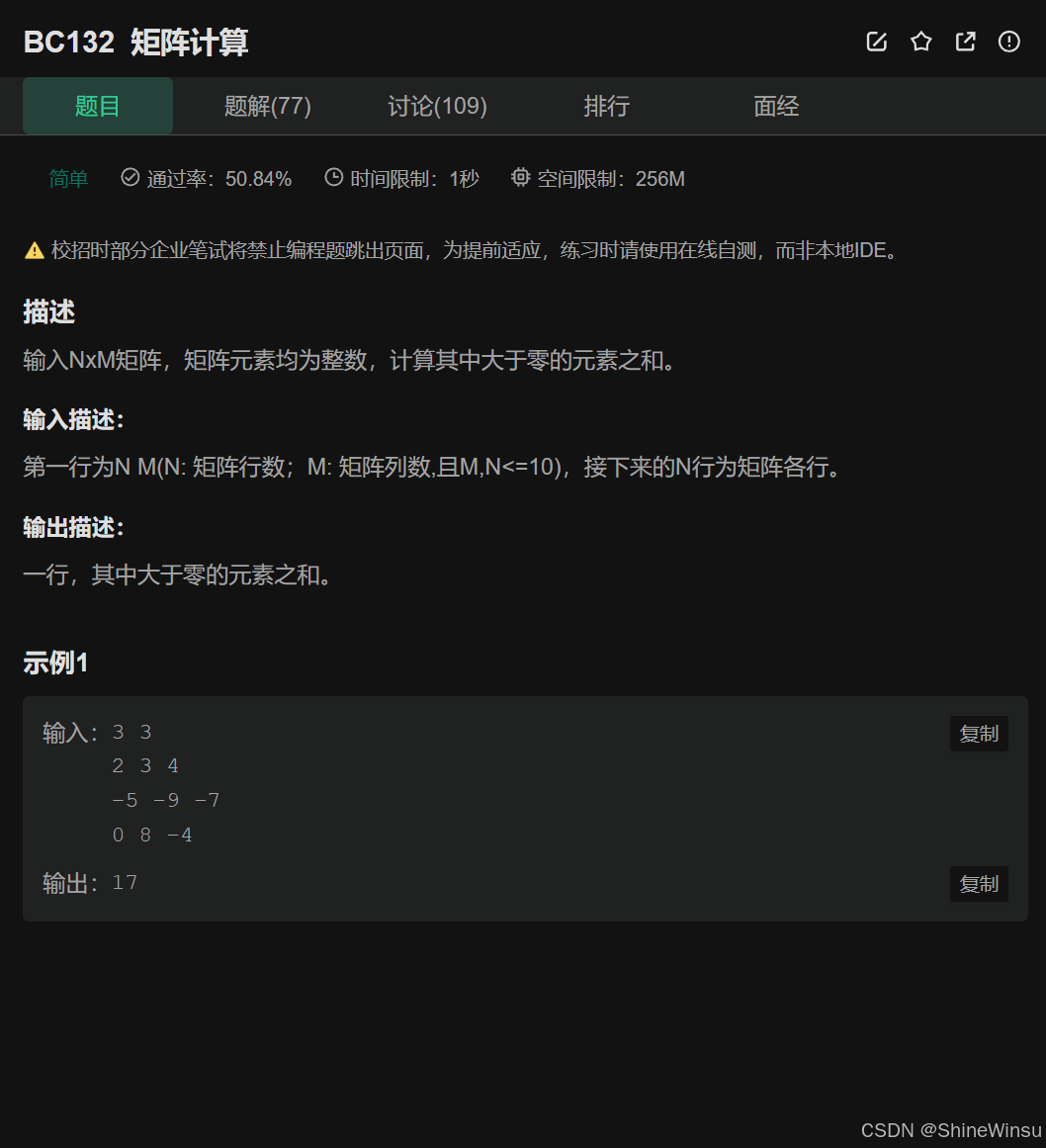
输入一个 N 行 M 列的整数矩阵，计算其中所有大于 0 的元素的和，并输出该和。

输入规则

第一行输入两个整数 N 和 M，分别表示矩阵的行数和列数（要求 N, M ≤ 10）。
接下来输入 N 行数据，每行有 M 个整数，作为矩阵的每一行元素。

输出规则

输出一行，内容为矩阵中所有大于 0 的元素的总和。

示例理解（以示例 1 为例）

输入矩阵为 3 行 3 列：
第一行：2 3 4（三个元素都大于 0）；
第二行：-5 -9 -7（均小于 0，不计入和）；
第三行：0 8 -4（只有8大于 0）。
大于 0 的元素是 2、3、4、8，总和为 2+3+4+8 = 17，与输出 “17” 一致。

简单来说，程序需要完成 “读取矩阵 → 筛选大于 0 的元素 → 累加这些元素 → 输出总和” 的流程。

这道题大家可以自己判断判断有没有陷阱。

继续解答：

下面我们就看看，解答这道题需要的步骤：

步骤 1：读取矩阵规模并初始化存储结构

输入两个整数 n 和 m，分别表示矩阵的行数和列数（例如输入 3 3，表示 3 行 3 列的矩阵）。
定义二维数组 arr[100][100] 用于存储矩阵元素，初始化为 0，预留足够空间容纳最大规模的矩阵。

步骤 2：按 “1 开始索引” 读取矩阵元素

使用嵌套循环读取矩阵的所有元素：外层循环变量 i 从 1 遍历到 n（对应题目中的 “第 1 行到第 n 行”），内层循环变量 j 从 1 遍历到 m（对应 “第 1 列到第 m 列”）。
将读取到的每个元素存入 arr[i][j]（例如第 2 行第 3 列的元素存到 arr[2][3]），数组的 arr[0][...] 和 arr[...][0] 位置不存储有效数据（闲置）。

步骤 3：筛选并累加大于 0 的元素

初始化累加变量 sum 为 0，用于存储所有大于 0 的元素之和。
再次通过嵌套循环遍历矩阵：i 从 1 到 n，j 从 1 到 m，逐个判断 arr[i][j] 的值。
若元素值大于 0（arr[i][j] > 0），则将该元素值累加到 sum 中；若元素小于或等于 0，则不进行累加。

步骤 4：输出累加结果

循环结束后，sum 中已存储矩阵中所有大于 0 的元素的总和，直接打印 sum 即可。

完美解决本题，依旧是完整代码：

#include <stdio.h>int main()
{int n, m;scanf("%d%d", &n, &m);int arr[100][100] = { 0 };for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &arr[i][j]);}}int sum = 0;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (arr[i][j] > 0){sum += arr[i][j];}}}printf("%d",sum);return 0;
}

由于题目比较简单，所以我依然就不提供详细注释了，相信大家一定可以看懂，如果依然不懂，可以再去仔细研究一下上文。

BC135 图像相似度：

这道题也只是上面某一题的翻版罢了，大家可以猜猜是哪一题，我们先看题目：

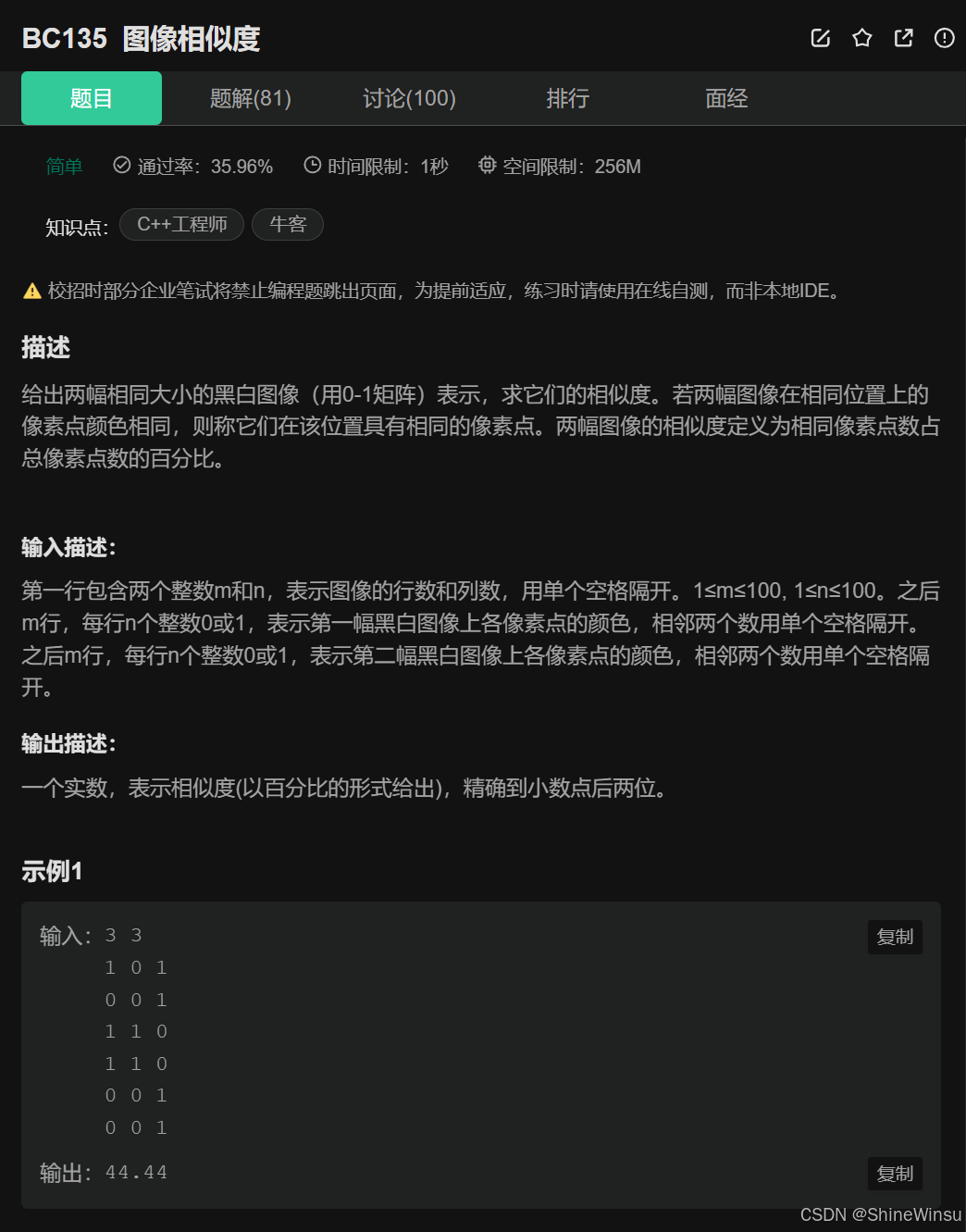
题意分析：

这道题的题意可从输入、处理逻辑、输出三方面分析：

输入部分

第一行输入两个整数 m 和 n，表示黑白图像的行数（m 行）和列数（n 列），两幅图像尺寸相同。
接下来输入 m 行，每行 n 个整数（0 或 1），表示第一幅图像的像素矩阵。
再输入 m 行，每行 n 个整数（0 或 1），表示第二幅图像的像素矩阵。

处理逻辑

需要计算两幅图像的相似度：

相似度定义为：相同位置像素值相同的点数 占 总像素点数（总像素数为 m×n）的百分比。
具体操作：遍历两幅图像的每个对应位置（第 i 行第 j 列），统计 “像素值相同” （即在两个数组在同一位置元素相同的数量）的位置数量，再除以总像素数，得到相似度（百分比形式）。

输出部分

输出一个实数，表示相似度，精确到小数点后两位（例如示例中输出 44.44）。

简言之，题目核心是 “比较两幅同尺寸黑白图像的像素矩阵，统计相同像素的占比并以百分比、两位小数形式输出”。

继续解答：

经过了分析之后，大家不难看出，本题不难，那么接下来我们需要哪些步骤去解答本题呢？

步骤 1：读取图像尺寸并初始化存储结构

输入两个整数 n 和 m，分别表示两幅图像的行数和列数（例如输入 3 3，表示图像为 3 行 3 列，共 9 个像素）。
定义两个二维数组 arr1[100][100] 和 arr2[100][100]，分别用于分别存储两幅图像的像素数据，初始化为 0，预留足够空间。

步骤 2：读取第一幅图像的像素数据

使用嵌套套循环读取第一幅图像的所有像素：外层循环变量 i 从 1 遍历到 n（对应 “第 1 行到第 n 行像素”），内层循环变量 j 从 1 遍历到 m（对应 “第 1 列到第 m 列像素”）。
将读取到的像素值（0 或 1）存入 arr1[i][j]（例如第 2 行第 3 列的像素存到 arr1[2][3]），数组的 arr1[0][...] 和 arr1[...][0] 位置闲置（不存储有效数据）。

步骤 3：读取第二幅图像的像素数据

用与步骤 2 完全相同的方式，读取第二幅图像的像素数据：i 从 1 到 n，j 从 1 到 m，将像素值存入 arr2[i][j]（例如第 1 行第 1 列的像素存到 arr2[1][1]）。

步骤 4：统计相同像素的数量并计算相似度

初始化计数器 count 为 0，用于记录两幅图像中 “对应位置像素值相同” 的点数。
遍历两幅图像的所有对应像素：i 从 1 到 n，j 从 1 到 m，若 arr1[i][j] 与 arr2[i][j] 的值相等（均为 0 或均为 1），则 count 加 1。
计算相似度：用 “相同像素点数 count” 除以 “总像素数 n×m”，再乘以 100 转换为百分比（例如总像素 9 个，相同像素 4 个，相似度为 4/9×100≈44.44）。

步骤 5：按格式输出相似度

使用 %.2f 格式控制符，将计算得到的相似度以 “保留两位小数” 的形式输出（例如输出 44.44）。

即如上，这道题唯一的难点可能就在于要如何去表达出百分数，那么也不难，首先我们需要注意的第一点就是，相似度极大概率是小数，所以我们得用浮点型去接收相似度结果，而且为了避免整型之间相除自动去尾（相同元素个数肯定是整型，而元素个数也是整型），我们就必须让相除的某一方为浮点型变量，而总元素个数已经在之前被指定格式完了，所以我们只能对相同元素个数下手，也就是count，我们把count变量设置为浮点型变量，这样便可以避免相除自动去尾。

至于如何实现百分数表达，自然是简单，对相除后的结果乘100就行了，因为相除的结果为0.nn，而百分数是nn.nn%，所以只需要*100即可。

由此，本题结束，下面是完整代码：

#include <stdio.h>int main()
{int n, m;scanf("%d%d", &n, &m);int arr1[100][100] = { 0 };int arr2[100][100] = { 0 };for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &arr1[i][j]);}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &arr2[i][j]);}}float count = 0;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (arr1[i][j] == arr2[i][j]){count++;}}}float same = (count / (n * m))*100;printf("%.2f",same);return 0;
}

由于题目比较简单，所以我依然就不提供详细注释了，相信大家一定可以看懂，如果依然不懂，可以再去仔细研究一下上文。

BC138 矩阵转置：

这道题难吗？其实不难，关键在于思维的转换，我们看题目：

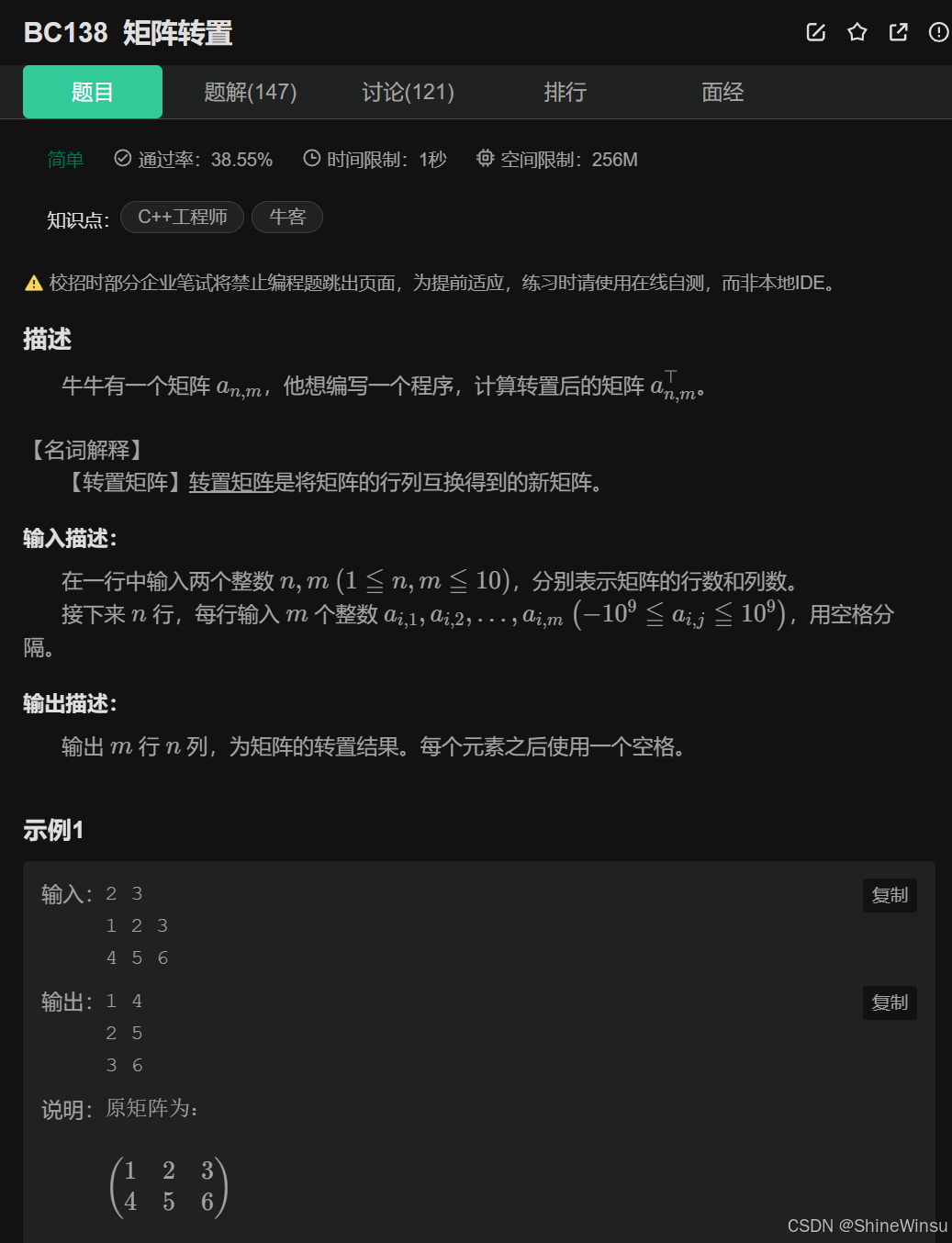
题意分析：

这道题的题意可从核心任务、输入、输出三方面分析：

核心任务

对给定的 n 行 m 列的矩阵，计算其转置矩阵（转置矩阵的定义是 “将原矩阵的行与列互换得到的新矩阵”）。

输入规则

第一行输入两个整数 n 和 m，分别表示原矩阵的行数和列数（要求 1 ≤ n, m ≤ 10）。
接下来输入 n 行数据，每行有 m 个整数，作为原矩阵的每一行元素（元素范围为 -10⁹ 到 10⁹）。

输出规则

输出转置后的矩阵：

转置矩阵的尺寸为 m 行 n 列（原矩阵的 “列数” 变为转置矩阵的 “行数”，原矩阵的 “行数” 变为转置矩阵的 “列数”）。
每个元素输出后紧跟一个空格，最终输出 m 行数据。

示例理解（以示例 1 为例）

原矩阵为 2 行 3 列：
第 1 行：1 2 3
第 2 行：4 5 6
转置后，原矩阵的 “行” 变为转置矩阵的 “列”，因此转置矩阵为 3 行 2 列：
第 1 行：1 4（原矩阵第 1 列的两个元素）
第 2 行：2 5（原矩阵第 2 列的两个元素）
第 3 行：3 6（原矩阵第 3 列的两个元素）

简言之，程序需要完成 “读取原矩阵 → 按转置规则生成新矩阵 → 按格式输出转置矩阵” 的流程

继续解答：

那么这道题，要怎么解决呢？看起来确实真的很难有思路，但是，只是看起来，既然看着没有思路，那我们就写、就画，总归会有一些想法，比干瞪眼好多了，所以，我们就来仔细观察题目所给示例的每一个数据的坐标吧

数据	坐标
1	(0,0)
2	(0,1)
3	(0,2)
4	(1,0)
5	(1,1)
6	(1,2)

这是横着的时候的各个元素所对应的坐标，光看这个没什么感觉，我们再比对一下竖着的时候，各个元素的坐标：

数据	坐标
1	(0,0)
4	(0,1)
2	(1,0)
5	(1,1)
3	(2,0)
6	(2,1)

看来之后还是没什么感觉，那我们不妨把这两个数组相同元素的各自坐标拿来进行比较呢：

元素值	arr1 中的坐标	arr2 中的坐标
1	(0,0)	(0,0)
2	(0,1)	(1,0)
3	(0,2)	(2,0)
4	(1,0)	(0,1)
5	(1,1)	(1,1)
6	(1,2)	(2,1)

这一下，不相信大家会看不出端倪来，我们其实就可以发现：

观察表格里的每个元素：

元素 1：arr1 中坐标 (0,0)，arr2 中坐标 (0,0)（i=j=0，互换后不变）；
元素 2：arr1 中坐标 (0,1)，arr2 中坐标 (1,0)（i=0,j=1 互换为 j=1,i=0）；
元素 3：arr1 中坐标 (0,2)，arr2 中坐标 (2,0)（i=0,j=2 互换为 j=2,i=0）；
元素 4：arr1 中坐标 (1,0)，arr2 中坐标 (0,1)（i=1,j=0 互换为 j=0,i=1）；
元素 5：arr1 中坐标 (1,1)，arr2 中坐标 (1,1)（i=j=1，互换后不变）；
元素 6：arr1 中坐标 (1,2)，arr2 中坐标 (2,1)（i=1,j=2 互换为 j=2,i=1）。

所以，我们就能推出如何实现转置矩阵了，那就是把原本元素的坐标（arr[i][j]）互相对调，变为arr[j][i]，除此之外，我们还需要更改循环的条件，在输入时，我们是按照横着的去输入，要求行i小于所输入原数组的行数n（j也是），但是在输出转置矩阵的时候，我们就不能再用这个条件了，既然元素坐标对调，那么对i和j的限制条件也得进行对调，（可以这么想：原本是2行3列，后面是3行2列，这不正是行和列的数量对调（即i和j的限制条件互调了）），大家如果不是很能理解这句话，不妨对照着上文的表格以及下文的详细注释版代码进行参考，这么一来，才可以正常实现转置矩阵。

在表达时，我们表达arr[j][i]即可（这里的j我们认定为列，i认定为行）。

由此，这道题也就能解决了，下面是完整代码：

#include <stdio.h>int main()
{int m = 0;int n = 0;scanf("%d%d",&n,&m);int arr[n][m] ; //不必初始化for(int i = 0;i<n;i++){for(int j = 0;j<m;j++){scanf("%d ",&arr[i][j]);}}for(int i = 0;i<m;i++){for(int j = 0;j<n;j++){printf("%d ",arr[j][i]);}printf("\n");}return 0;
}

考虑到这道题稍微难一些，这边给出一版详细注释代码：

#include <stdio.h>int main()
{// 1. 定义变量存储矩阵的行数和列数// n：用于存储原矩阵的行数（后续作为外层循环控制行的遍历）// m：用于存储原矩阵的列数（后续作为外层循环控制列的遍历）int m = 0;int n = 0;// 2. 读取原矩阵的行数n和列数m// 输入格式示例：若原矩阵是2行3列，输入为 "2 3"scanf("%d%d", &n, &m);// 3. 定义二维数组存储原矩阵// arr[n][m]：变长数组（VLA），行数为n，列数为m，大小由输入的n和m动态决定// 注：变长数组在C99标准中支持，部分编译器需开启对应支持；题目未要求初始化，故不初始化int arr[n][m]; // 4. 读取原矩阵的元素，存入二维数组arr// 外层循环：控制行数，i从0到n-1（数组索引从0开始，对应原矩阵第1行到第n行）for (int i = 0; i < n; i++){// 内层循环：控制列数，j从0到m-1（对应原矩阵第1列到第m列）for (int j = 0; j < m; j++){// 读取单个元素，存入arr[i][j]（i行j列的位置）// 格式符后加空格：避免输入时因换行/空格导致的读取异常（兼容不同输入分隔方式）scanf("%d ", &arr[i][j]);}}// 5. 输出原矩阵的转置矩阵// 转置矩阵的核心规律：原矩阵的“列”变为转置矩阵的“行”，原矩阵的“行”变为转置矩阵的“列”// 外层循环：控制转置矩阵的行数（=原矩阵的列数m），i从0到m-1for (int i = 0; i < m; i++){// 内层循环：控制转置矩阵的列数（=原矩阵的行数n），j从0到n-1for (int j = 0; j < n; j++){// 关键：原矩阵arr[j][i]（j行i列）对应转置矩阵的i行j列// 输出元素后加空格，保证每个元素间有分隔printf("%d ", arr[j][i]);}// 每输出完转置矩阵的一行（即原矩阵的一列），换行，确保格式正确printf("\n");}return 0;
}

BC137 序列重组矩阵：

最后讲的这道题目，其实也不难，但是对它，我有三种方法，每个方法都各有自己的优势，所以我这边想要全部讲一讲，我们先看题目：

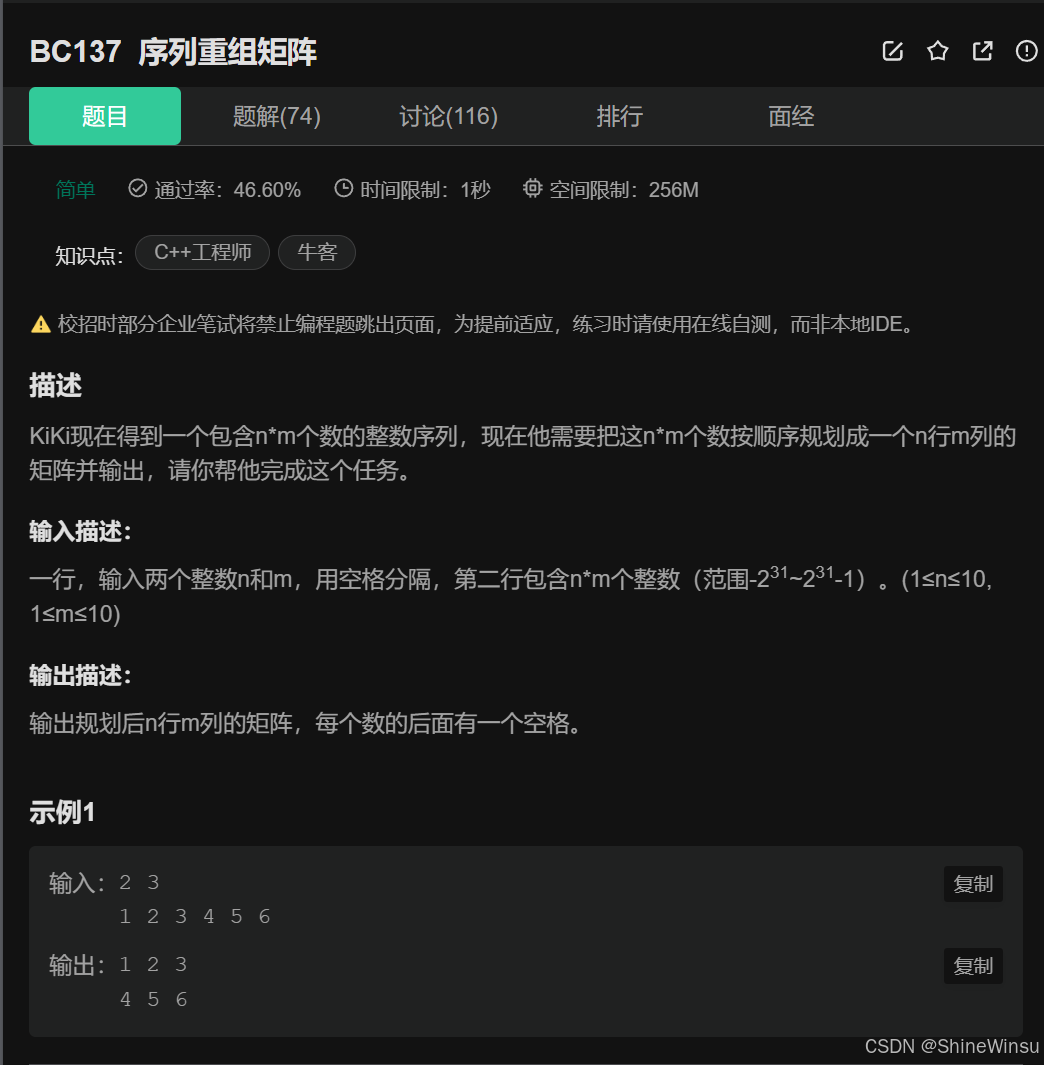
题意分析：

这道题的题意可从输入、处理要求、输出三个部分来分析：

输入部分

第一行输入两个整数 n 和 m，用空格分隔，分别表示要规划成的矩阵的行数和列数（例如输入 2 3，表示要规划成 2 行 3 列的矩阵）。
第二行输入 n×m 个整数（范围为 -2³¹ ~ 2³¹-1），这是需要被规划成矩阵的整数序列（例如输入 1 2 3 4 5 6，共 2×3 = 6 个整数）。

处理要求

将第二行输入的 n×m 个整数按顺序规划成一个 n 行 m 列的矩阵。具体来说：

序列的前 m 个整数作为矩阵的第 1 行；
接下来的 m 个整数作为矩阵的第 2 行；
以此类推，直到填满 n 行。

输出部分

输出规划后的 n 行 m 列矩阵，每个数后面有一个空格（例如示例中，输入序列 1 2 3 4 5 6 规划成 2 行 3 列后，输出第 1 行为 1 2 3 ，第 2 行为 4 5 6 ）。

简单来说，题目核心是 “把一维整数序列按顺序填充为二维矩阵，并按行输出”。

方法一：

这第一个方法，其实有点麻烦了，但是其中蕴含的思维，还是不错的。

5 个核心环节，通过 “先存储一维序列，再按行拆分输出” 的方式，将一维整数序列转换为指定行列的矩阵，具体如下：

步骤 1：读取矩阵规模并计算总元素数

输入两个整数 n 和 m，分别表示目标矩阵的行数和列数（例如输入 2 3，表示要生成 2 行 3 列的矩阵）。
计算总元素数量 sum = n × m（即一维序列的长度，如 2 行 3 列的矩阵总元素数为 6）。

步骤 2：定义一维数组并存储输入序列

定义一维数组 arr[100]（初始化为 0），用于存储输入的整数序列（题目限制 n、m ≤ 10，因此 sum ≤ 100，数组空间足够）。
使用循环从输入中读取 sum 个整数，按顺序存入 arr[1] 到 arr[sum]（注意：数组从索引 1 开始存储，arr[0] 闲置）。

步骤 3：初始化标记变量用于拆分序列

定义标记变量 sign 并初始化为 1，用于记录 “当前行需要输出的第一个元素在一维数组中的索引”（初始指向序列的第一个元素）。

步骤 4：按行拆分并输出矩阵

外层循环控制行数：i 从 1 遍历到 n（对应矩阵的第 1 行到第 n 行）。
内层循环负责输出当前行的元素：
- 从 sign 开始遍历数组，逐个输出 arr[j] 并加空格分隔；
- 当 j 是 m 的倍数时（即已输出 m 个元素，填满一行），更新 sign 为 j + 1（指向下行第一个元素），并通过 goto huan 跳出内层循环

这一步是这个方法的关键所在，我们先来了解一下goto语句

goto语句介绍：

goto 语句是一种在编程语言中用于无条件跳转的语句，在 C、C++ 等语言中都有支持。以下是关于 goto 语句的详细介绍：

语法格式

在 C 语言中，goto 语句的基本语法形式为：

goto 标签;
// 其他代码
标签:
// 标签所在位置的代码

其中，标签 是程序员自定义的标识符，用来标记程序中的某个位置，goto 语句会使程序的执行流程无条件地跳转到指定标签所在的位置继续执行。

执行流程

当程序执行到 goto 语句时，会立即停止当前位置的执行，直接跳转到指定的标签处，接着执行标签后面的代码。例如：

#include <stdio.h>int main() {int i = 0;
start:printf("i = %d\n", i);i++;if (i < 5) {goto start;}return 0;
}

在上述代码中，程序首先执行到 start 标签处，打印 i 的值，然后 i 自增。接着判断 i 是否小于 5，如果条件成立，执行 goto start 语句，程序的执行流程又跳回到 start 标签处，继续循环打印，直到 i 不小于 5 为止。

优点

快速跳出多层循环：在一些复杂的嵌套循环结构中，如果需要满足特定条件时立即跳出多层循环，使用 goto 语句可以直接实现，而不需要使用多层 break 语句或设置额外的标志变量。例如：

#include <stdio.h>int main() {int i, j;for (i = 0; i < 3; i++) {for (j = 0; j < 3; j++) {if (i * j == 4) {goto out;  // 直接跳出两层循环}printf("i = %d, j = %d\n", i, j);}}
out:printf("Out of loops\n");return 0;
}

错误处理：在处理资源释放等错误情况时，goto 语句可以方便地跳转到统一的错误处理代码块，确保资源被正确释放。比如在涉及文件操作、内存分配的代码中：

#include <stdio.h>
#include <stdlib.h>int main() {FILE *fp = fopen("test.txt", "r");if (fp == NULL) {perror("fopen");return 1;}int *arr = (int *)malloc(10 * sizeof(int));if (arr == NULL) {fclose(fp);perror("malloc");return 1;}// 假设中间有其他复杂操作// 错误发生时统一释放资源并跳转处理if (/* 某种错误条件 */) {free(arr);fclose(fp);goto error;}// 正常的后续操作free(arr);fclose(fp);return 0;
error:printf("An error occurred and resources have been released.\n");return 1;
}

缺点

破坏程序的结构性：goto 语句可以随意跳转，可能会使程序的执行流程变得复杂和难以理解，尤其是在大型程序中，容易导致代码的逻辑混乱，可读性变差。例如，如果在一个函数中有多个 goto 语句相互跳转，不同的跳转路径交织在一起，会让阅读代码的人很难理清代码的执行顺序。
增加调试难度：由于 goto 语句破坏了程序的结构化，在调试过程中，很难通过正常的代码执行顺序来跟踪变量的值和程序的执行流程，增加了定位和解决问题的难度。
不利于代码维护：当程序需要修改或扩展功能时，含有大量 goto 语句的代码可能会因为一处修改而影响到其他位置的执行逻辑，牵一发而动全身，导致维护成本大幅增加。

这里使用goto语句的目的就是要在表达完一行后（当表达的j到了要表达的列数的大小）进行换行表达下一行，如下代码：

for (int i = 1; i <= n; i++)//表示要打印几行
{for (int j = 1; j <= sum; j++)//遍历一维数组所有元素，但是要在接下来的代码实现表达完想要的列数之后就进行换行{printf("%d ", arr[j]);if (j % m == 0)//当到达一行尾部时{goto huan;}}
huan:printf("\n");
}

这么使用goto语句之后，换行是换行了，可是在表达完换行之后，下一行的表达却是与上一行一样，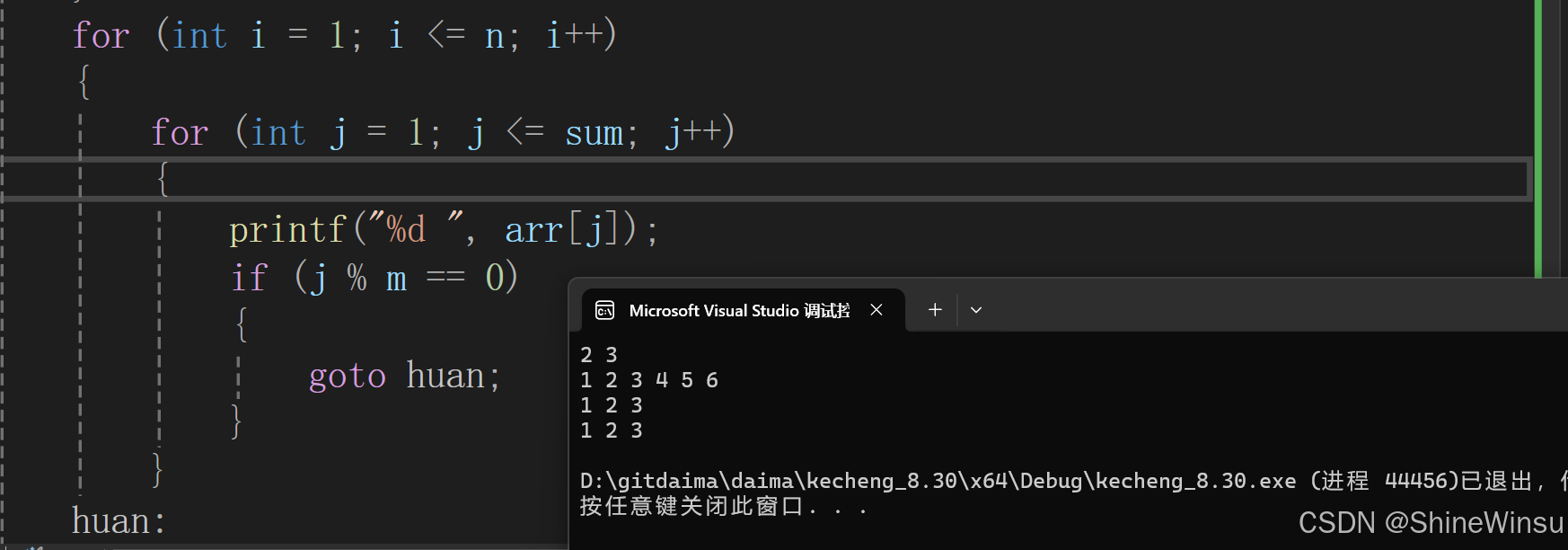

这是为什么呢？其实很简单，我们可以调试一下就知道了，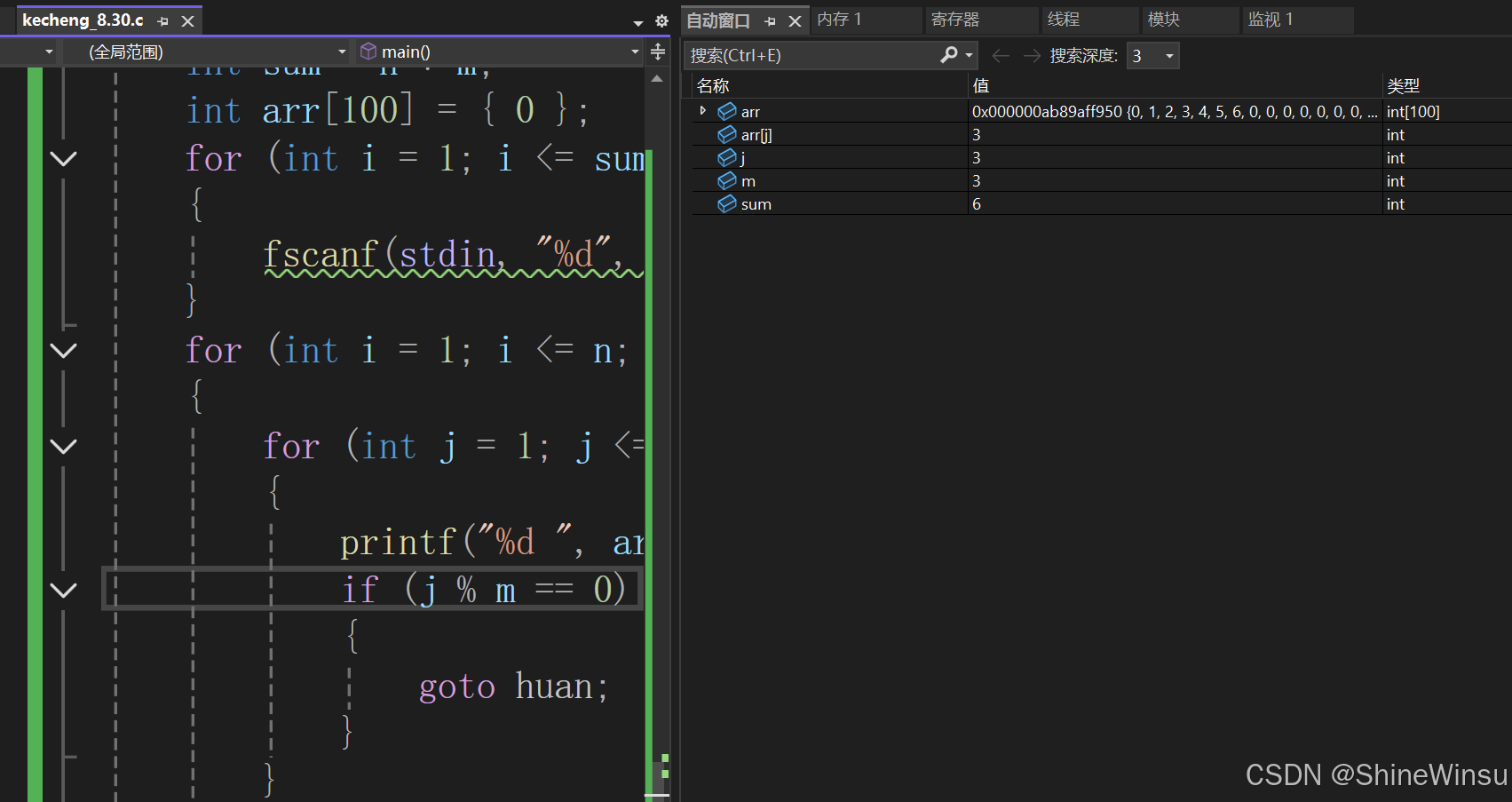

此时已经到了一行，我们要进行换行操作了，可以看到j为3了，按道理来说在进行换行之后，j就应该为4了，即表达一维数组第4个元素了，那么当我们进行下一步，真的会这样子吗？

可以看到，j变为1了，是的，j又从头开始了，这可怎么办？这样子可不行，没事，不用担心，我们设一个变量去接收表达完一行后的j+1（要记得是j+1，进入到下一个元素，不难下一轮循环，还是会表达一个与上一个循环最后一个被表达的元素相同的数据）不就行了，再让下一轮循环的j从这个变量开始，不就能够实现上面我们所讲的正确过程了，代码如下：

int sign = 1;
for (int i = 1; i <= n; i++)
{for (int j = sign; j <= sum; j++){printf("%d ", arr[j]);if (j % m == 0){sign = j + 1;goto huan;}}
huan:printf("\n");
}

如下是对这段代码的详细解释：

1. 先搞懂 `sign` 的作用 ——“每行起始位置的导航标”

int sign = 1; 初始化时，sign 指向一维数组 arr 的第 1 个元素（因为数组从索引 1 存储数据），它的核心功能是：记录当前要输出的 “某一行”，在一维数组中从哪个位置开始取元素。

比如目标是 2 行 3 列矩阵（n=2，m=3，sum=6）：

第 1 行输出前 3 个元素，sign 初始为 1，所以内层循环从 j=1 开始；
第 1 行输出完（j=3 时，3%3==0），sign 被更新为 3+1=4，为第 2 行从 j=4 开始输出做准备；
第 2 行输出时，内层循环直接从 j=4 开始，取到 j=6 后完成输出，逻辑闭环。

2. 内层循环的 “精准停止”—— 靠 `j%m == 0` 和 `goto`

内层循环 for (int j = sign; j <= sum; j++) 看似是遍历整个数组，但其实有 “强制刹车” 机制：

每次打印 arr[j] 后，判断 j%m == 0：因为每行要输出 m 个元素，当 j 是 m 的倍数时，就说明当前行已经打印完 m 个元素了（比如 m=3 时，j=3、6、9... 都是换行点）；
一旦满足条件，先更新 sign = j+1（把下一行的起始位置记下来），再用 goto huan 直接跳出内层循环 —— 避免内层循环继续往后遍历，精准控制 “一行只打印 m 个元素”。

3. `huan` 标签的 “收尾工作”—— 换行对齐

huan: 标签刚好在两层循环之间，且和外层循环同缩进：

每次 goto huan 跳出内层循环后，都会执行 printf("\n")，也就是打印完一行后立刻换行，保证输出的矩阵是 “每行 m 个元素，共 n 行” 的规范格式；
哪怕极端情况（比如最后一行刚好打印到 sum 个元素），循环结束后也会执行换行，不会出现格式错乱。

举个具体例子（n=2，m=3，sum=6，arr [1~6] = [1,2,3,4,5,6]）：

第 1 次外层循环（i=1）：
- j 从 sign=1 开始，打印 arr [1]=1、arr [2]=2、arr [3]=3；
- j=3 时，3%3==0，sign 更新为 4，goto huan，执行换行；
第 2 次外层循环（i=2）：
- j 从 sign=4 开始，打印 arr [4]=4、arr [5]=5、arr [6]=6；
- j=6 时，6%3==0，sign 更新为 7，goto huan，执行换行；
外层循环 i=3 时不满足 i<=2，循环结束，最终输出：
plaintext
```
1 2 3 
4 5 6 
```

每次内层循环结束后（huan 标签处），输出换行符，完成一行的输出。

步骤 5：完成所有行输出后程序结束

当外层循环遍历完 n 行后，所有元素按 n 行 m 列的格式输出完毕，程序返回 0 结束。

整个流程的核心是通过 sign 标记每行的起始位置，结合 j % m == 0 判断是否填满一行，实现了 “一维序列→二维矩阵” 的转换输出，逻辑清晰地完成了题目要求。

看完上面的解释，大家应该就清楚这个方法一了，我们直接上代码：

#include <stdio.h>int main()
{int n, m;scanf("%d%d", &n, &m);int sum = n * m;int arr[100] = { 0 };for (int i = 1; i <= sum; i++){fscanf(stdin, "%d", &arr[i]);}int sign = 1;for (int i = 1; i <= n; i++){for (int j = sign; j <= sum; j++){printf("%d ", arr[j]);if (j % m == 0){sign = j + 1;goto huan;}}huan:printf("\n");}return 0;
}

再给上详细注释：

#include <stdio.h>int main()
{// 定义变量存储矩阵的行数(n)和列数(m)int n, m;// 从标准输入读取n和m的值（例如输入"2 3"表示2行3列的矩阵）scanf("%d%d", &n, &m);// 计算需要存储的总元素数量：行数×列数int sum = n * m;// 定义一维数组arr，大小为100（满足题目中n、m≤10的要求，sum≤100）// 初始化为0，避免未初始化的随机值影响int arr[100] = { 0 };// 循环读取sum个整数，存储到数组arr中（从索引1开始存储，arr[0]闲置）for (int i = 1; i <= sum; i++){// 使用fscanf从标准输入(stdin)读取整数，存入arr[i]fscanf(stdin, "%d", &arr[i]);}// 定义标记变量sign，记录当前行需要输出的第一个元素在数组中的索引// 初始值为1，表示从数组的第一个有效元素开始int sign = 1;// 外层循环：控制输出矩阵的行数（从1到n行）for (int i = 1; i <= n; i++){// 内层循环：从sign标记的位置开始，输出当前行的元素for (int j = sign; j <= sum; j++){// 输出数组中的元素，并在后面加一个空格printf("%d ", arr[j]);// 判断是否已输出m个元素（即当前行是否已满）// j % m == 0表示当前已输出m个元素（因为每行需要m个元素）if (j % m == 0){// 更新sign为下一行第一个元素的索引（当前位置的下一个）sign = j + 1;// 使用goto跳转到huan标签，跳出内层循环，避免继续输出goto huan;}}// 标签huan：用于接收goto跳转，执行换行操作huan:// 输出换行符，完成当前行的输出，准备输出下一行printf("\n");}return 0;
}

如上

方法二：

这个方法就会简单多了，先直接给大家看代码，然后再进行解释：

#include <stdio.h>int main()
{int n = 0;int m = 0;int arr[100] = { 0 };scanf("%d %d", &n, &m);for (int i = 0; i < n; i++){for (int j = 0; j < m; j++){scanf("%d", &arr[i]);printf("%d ", arr[i]);}printf("\n");}return 0;
}

这段代码的主要功能是读取一个 n 行 m 列的矩阵元素，并即时打印出这个矩阵，但代码中存在逻辑问题。以下是详细解释：

1. 变量定义与初始化

int n = 0;       // 用于存储矩阵的行数
int m = 0;       // 用于存储矩阵的列数
int arr[100] = {0};  // 定义一个大小为100的一维数组，初始化为0

n 和 m 分别表示矩阵的行数和列数
arr 是一个一维数组，本意可能是用于临时存储矩阵元素（但实际使用存在问题）

2. 读取矩阵的行数和列数

scanf("%d %d", &n, &m);  // 从输入读取n和m的值，例如输入"2 3"表示2行3列

3. 读取并打印矩阵元素（核心逻辑）

// 外层循环：控制行数（从0到n-1，共n行）
for (int i = 0; i < n; i++)
{// 内层循环：控制列数（从0到m-1，共m列）for (int j = 0; j < m; j++){scanf("%d", &arr[i]);  // 读取一个元素，存入数组的第i个位置printf("%d ", arr[i]); // 打印刚读取的元素，加空格分隔}printf("\n");  // 一行打印完后换行
}

但是这个方法真的好吗？答案是：不好

4. 代码存在的问题

数组使用错误：
代码试图用一维数组 arr[i] 存储二维矩阵的元素，但逻辑上有问题。当内层循环（列循环）执行时，会多次覆盖 arr[i] 的值（例如第 1 行的 3 列元素会连续存入 arr[0]，后一个值会覆盖前一个）。
实际效果是：每行最终只保存了最后一个输入的元素，但打印时因为是即时输出，所以表面上能看到完整的矩阵（打印的是刚输入的值，而非数组中保存的值）。
内存浪费：
若要正确存储 n 行 m 列的矩阵，应使用二维数组（如 arr[n][m]），或按顺序存储在一维数组中（如 arr[i*m + j]）。当前的一维数组使用方式不符合逻辑。

5. 代码的实际效果

假设输入：

2 3
1 2 3
4 5 6

代码会输出：

1 2 3 
4 5 6

表面上能得到正确的矩阵，但数组 arr 中实际存储的是 [3, 6, 0, ...]（仅保存了每行最后一个元素）。这是因为打印操作在覆盖之前执行，掩盖了数组存储的逻辑错误。

所以这也是为什么我直接就给大家看代码，我个人并不推荐这个方法。

方法三：

这个方法，那就是最本质的方法了，大家可能一直觉得，对于二维数组的输入，必须要遵循换行的操作，在到了该换行的时候，我们就得回车一下，换行后再输入，类似这么输入：

但是真的需要这样子吗？

其实是不需要的，是的，我们不换行输入，也是可以正常把数据存储进二维数组中的，也就是说，我们可以直接这么对二维数组进行数据输入：，那么这么一来，这道题，不就是毫无难度了吗？

我们创建一个二维数组，然后就用输入一维数组的方式一行的输入数据，最后再使用二维数组的方式表达就行，代码如下：

int main()
{int m = 0, n = 0;scanf("%d%d", &m, &n);int arr[100][100] = { 0 };int i = 0, h = 0, k = 0;for (h = 0; h < m; h++){for (k = 0; k < n; k++){scanf("%d", &arr[h][k]);}}int a = 0, s = 0;for (a = 0; a < m; a++){for (s = 0; s < n; s++){printf("%d ", arr[a][s]);}printf("\n");}return 0;
}

如上，完美解决本题。

结语：

到这里，牛客网二维数组基础题目的解析就全部结束了。这 8 道题看似简单，却几乎覆盖了二维数组的核心基础用法 —— 从数据存储、遍历访问，到索引转换、格式输出，甚至包含了一维数组与二维数组的转换逻辑。对初学者而言，这些题目不是 “难题”，却是 “基石”：通过它们，你能亲手验证二维数组的内存连续性、理解索引计数差异的陷阱、掌握嵌套循环的控制逻辑，而这些细节恰恰是后续解决复杂矩阵问题（如矩阵乘法、动态规划）的关键。

当你逐行敲完这 8 道题的代码，或许会发现：二维数组的核心逻辑，本质上是 “用两个维度管理有序数据”—— 从学生成绩的行与科，到矩阵元素的行与列，再到图像像素的位置对应，本质都是 “行索引 + 列索引” 的精准定位与遍历。这些题目没有复杂的算法技巧，却藏着编程入门的 “底层逻辑”：如何把题目描述的 “人类习惯”（如 1 开始的行号）转化为 “代码规则”（如 0 开始的数组索引），如何用嵌套循环控制数据的读写顺序，如何通过变量记录中间结果（如总分、最高身高位置）。

对初学者而言，这些 “简单题” 的价值，远不止 “做出答案”。比如做 “矩阵元素定位” 时，你会真切感受到 “人类计数” 与 “代码索引” 的冲突，从此对 “数组越界”“索引转换” 有更直观的认知；做 “图像相似度” 时，你会明白 “百分比计算” 里浮点数精度的重要性，避免踩中 “整型除法自动截断” 的坑；做 “矩阵转置” 时，你会突然领悟 “行列互换” 不是抽象概念，而是 “arr [i][j] 变 arr [j][i]” 的具体操作。这些从 “理解” 到 “实践” 的跨越，才是编程能力提升的关键。

最后想提醒大家：不要因为题目简单就 “眼高手低”。编程的核心是 “逻辑落地”，哪怕是 “计算总分” 这样的简单需求，亲手敲代码时也可能遇到 “sum 忘记清零”“循环条件写错” 的小问题。而解决这些小问题的过程，正是构建 “代码严谨性” 的开始。如果此刻你已经能独立写出这些题目的代码，那么恭喜你，你已经掌握了二维数组的基础用法；如果还有卡顿，不妨回头再理一理 “输入 - 处理 - 输出” 的每一步，相信你很快就能找到突破点。

我们下一篇 “二维数组进阶题解” 再见，期待那时的你，已经能更从容地应对更复杂的挑战！

查看全文

http://www.xdnf.cn/news/19272.html