当前位置：首页 > backend >正文

相似度、距离

backend 2025/8/23 20:01:57

概述

之前在学习ES时有一个很重要的概念就是相似度，用于全文检索，参考ES系列之相似度模型。

最近学习LLM，RAG，遇到Embedding（嵌入）模型，又遇到相似度计算，参考Embedding入门概述。

相似度和距离是两个相关联的概念：距离越小，两个事物越相似；距离越大，两个事物越不相似。

相似度计算是一切分类、聚类、搜索、推荐、导航问题的前提。

聚类与分类没有本质区别：分类是事先有明确的类目体系的，聚类是事先没有明确的类目体系的，需要在聚类过程中边聚类边整理出类目体系。

相似问题是研究事物之间相似度或距离的计算过程，12种常见的相似模型：

欧几里得距离：两点之间的直线距离；
曼哈顿距离：城市街区或建筑物之间的行车距离；
切比雪夫距离：国际象棋中的距离计算；
闵可夫斯基距离：欧几里得距离、曼哈顿距离、切比雪夫距离的统一；
马哈拉诺比斯距离：与量纲无关的防维度相关性干扰的距离；
皮尔逊相关系数：两个变量的相关度计算模型；
杰卡德相似系数：两个集合的相似度计算模型；
余弦相似度：两个向量的相似度计算模型；
汉明距离：数据传输错误率的度量模型；
KL散度：两个概率分布的相似性度量模型；
海林格距离：两个概率分布的相似性度量的另一种模型；
编辑距离：一个字符串转换为另一个字符串需要的编辑操作数。

欧几里得距离

Euclidean Distance，简称欧氏距离，指欧几里得空间（Euclidean Space）中两个点之间的真实距离，或向量的自然长度（向量到原点的距离）。在2维或3维空间中，欧式距离就是常说的两点之间的线段距离。在许多早期文献中，也常被称为毕达哥拉斯距离。

欧式距离是最常用的距离计算方法。

计算公式： $d(A,B)=(y1−x1)2+(y2−x2)2+...+(yn−xn)2d(A,B)=\sqrt{(y_1-x_1)^2+(y_2-x_2)^2+...+(y_n-x_n)^2}$

曼哈顿距离

在导航场景下，再使用欧氏距离就没有什么实际意义，因为欧式距离是计算直线。导航领域，地点也叫兴趣点（Point of Interest，POI）。

曼哈顿距离，又叫出租车距离，绝对距离，街区距离，由赫尔曼·闵可夫斯基（Hermann Minkowski）所创的词汇，使用几何度量空间的几何学用语，标明两个点在标准坐标系上的绝对轴距总和。

在建立坐标体系后，两个点之间的曼哈顿距离是确定的，不会随着路线的变化而有差异；但如果坐标体系变化，则两个点之间的曼哈顿距离也可能会变化。在世界上桥梁最多的地方——贵州，会修建很多特大桥，目的就是调整坐标系（优化山里人的出行方式），减少曼哈顿距离。

2点之间的计算公式： $d_M(A,B)=|x_2-x_1|+|y_2-y_1|$

应用场景：

导航
早期计算机图像处理计算两点距离

切比雪夫距离

切比雪夫距离起源于国际象棋中国王的走法，每次只能往周围的8个方格走一步。
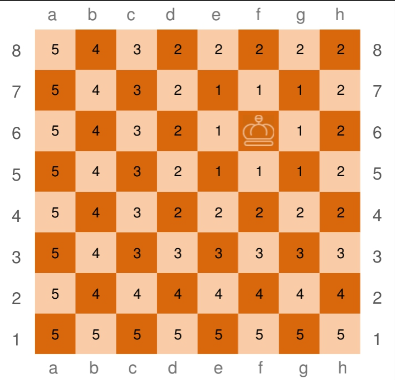
在这里插入图片描述
计算公式： $dC(A,B)=max⁡1≤i≤n(∣yi−xi∣)d_C(A,B)=\max_{1\leq i \leq n}(|y_i-x_i|)$

闵可夫斯基距离

在爱因斯坦提出狭义相对论后，其数学老师赫尔曼·闵可夫斯基将爱因斯坦与洛伦兹的理论结果重新表达为3+1维的时空，其中光速在各个惯性参考系皆为定值，这样的时空被称为闵可夫斯基空间；对于空间中的两点之间的距离，被称为闵可夫斯基距离、时空距离。

计算公式： $dMinkowski(x,y)=(∑i=1n∣xi−yi∣p)1pd_{Minkowski}(x,y)=\left( \sum_{i=1}^{n} \lvert x_i - y_i \rvert^p \right)^{\tfrac{1}{p}}$
其中， $p$ 为特定常数，当 $p$ =1时，演变为曼哈顿距离；当 $p$ =2时，演变为欧氏距离；当 $p$ 趋向于无穷大时，演变为切比雪夫距离。

马哈拉诺比斯距离

又马氏距离，由马哈拉诺比斯（P.C.Mahalanobis）提出的计算两个未知样本的相似度，一种对传统欧氏距离的改进方法。

欧氏距离不能很好地用于样本相似度计算的原因：

欧氏距离认为各维度之间是无量纲的，但实际生活中很多维度是有量纲；
欧氏距离认为各维度之间是相互独立的，但显然不是。

马哈拉诺比斯在欧氏距离的基础上提出两点改进：

消除相似度计算对原始数据的量纲的影响，使样本的相似度计算与数据的单位无关；
消除原始数据各维度之间的相关性干扰。

马氏距离的计算，相当于对样本数据在欧几里得空间加以坐标变换。计算各维度的均值，相当于找到转换后坐标体系中的新原点，通过协方差矩阵去掉各维度之间的相关性，并使得马氏距离与量纲无关。

理解马氏距离，需要有统计学基础，涉及如下概念：

均值：算术平均值，不能反映数据样本的全貌
方差：体现样本数据的波动性；是协方差的一种特殊情况
标准差：方差的算术平方根，也叫标准方差、均方差
协方差：两个变量的总体误差；正数值越大，两个变量就越正相关；负数值越大，两个变量就越负相关。
协方差矩阵：对称矩阵。

计算公式： $dMah(x⃗,y⃗)=(x⃗−y⃗)T∑−1(x⃗−y⃗)d_{Mah}(\vec{x},\vec{y})=\sqrt{(\vec{x}-\vec{y})^T\sum^{-1}(\vec{x}-\vec{y})}$
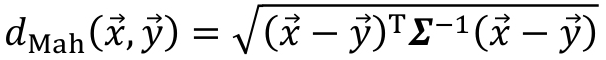
在这里插入图片描述

皮尔逊相关系数

Pearson Correlation Coefficient，相关相似性，用于衡量两个变量的线性相关程度。如果有两个变量X、Y，计算公式 $p(X,Y)=cov(X,Y)σXσYp(X,Y)=\frac{cov(X,Y)}{σ_Xσ_Y}$ ，对于计算结果的解读：

当皮尔逊相关系数为0时，X和Y两个变量无关系；
当X的值增大（或减小）时，Y的值也会增大（或减小），则这两个变量为正相关，皮尔逊相关系数为0～1.00；
当X的值增大（或减小）时，Y的值会减小（或增大），则这两个变量为负相关，皮尔逊相关系数为-1.00～0.00；
皮尔逊相关系数的绝对值越大，两个变量的相关性越强；皮尔逊相关系数越接近于1或-1，两个变量的相关性越强；皮尔逊相关系数越接近于0，相关性越弱。

杰卡德相似系数

Jaccard Similarity Coefficient，又称Jaccard相关系数，用于计算两个有限样本数据集之间的相似度。

对于两个有限集合A与B，其Jaccard系数计算公式： $Jaccard(A,B)=∣A⋂B∣∣A⋃B∣=∣A⋂B∣∣A∣+∣B∣−∣A⋂B∣Jaccard(A,B)=\frac{|A\bigcap B|}{|A\bigcup B|}=\frac{|A\bigcap B|}{|A|+|B|-|A\bigcap B|}$

应用：计算两个文本的相似性，电商网站的搜索引擎，论文查重的剽窃检测。在商品搜索中，集合的元素一般为词语；在剽窃检测中，集合的元素一般为Tri-gram，即前后相邻的3个词语。

在实际使用Jaccard相关系数时，一般还需要考虑集合中各元素权重，给重要的元素赋予更高权重。加权Jaccard相关系数计算公式： $Jaccard(A,B)=∑i∈A∩BWi∑j∈A∪BWjJaccard(A,B)=\frac{\sum_{i \in A \cap B} W_i}{\sum_{j \in A \cup B} W_j}$ ，其中， $W_i$ 表示集合 $A⋂BA\bigcap B$ 中元素 $i$ 的权重， $W_j$ 表示集合 $A⋃BA\bigcup B$ 中元素 $j$ 的权重。

在文本相似度的计算中，单词权重可使用TF-IDF模型，或其改进版本。

对于两个 $n$ 维向量 $x⃗\vec x$ 与 $y⃗\vec y$ ，令 $x⃗=[x1,x2,...,xn]\vec x=[x_1,x_2,...,x_n]$ ， $y⃗=[y1,y2,...,yn]\vec y=[y_1,y_2,...,y_n]$ ，则 $x⃗\vec x$ 与 $y⃗\vec y$ 的Jaccard相关系数定义为： $Jaccard(x⃗,y⃗)=∑i=1nmin(xi,yi)∑i=1nmax(xi,yi)Jaccard(\vec x,\vec y)=\frac{\sum_{i=1}^{n} min(x_i,y_i)}{\sum_{i=1}^{n} max(x_i,y_i)}$ ，一般被称为向量的广义Jaccard相关系数。

与欧式距离一样，用广义Jaccard相关系数计算身材相似度也受量纲的影响，更适合量纲一致的场景。

还可以定义两个函数的广义Jaccard相关系数： $Jaccard(f,g)=∫min(f,g)du∫max(f,g)duJaccard(f,g)=\frac{\int min(f,g)du}{\int max(f,g)du}$

余弦相似度

Cosine Similarity，在信息检索领域中使用最广泛的相似度计算模型。使用向量空间中两个向量的夹角的余弦值来表示两个向量的相似度。相比距离度量，余弦相似度更注重两个向量在方向上的差异，而非在长度上的差异。

对于两个 $n$ 维向量 $x⃗\vec x$ 与 $y⃗\vec y$ ，令 $x⃗=[x1,x2,...,xn]\vec x=[x_1,x_2,...,x_n]$ ， $y⃗=[y1,y2,...,yn]\vec y=[y_1,y_2,...,y_n]$ ，则 $x⃗\vec x$ 与 $y⃗\vec y$ 的余弦相似度系数 $sim(x⃗,y⃗)sim(\vec x,\vec y)$ 为： $sim(x⃗,y⃗)=cos(θ)=∑i=1nxiyi∑i=1nxi2∑i=1nyi2sim(\vec x,\vec y)=cos(\theta)=\frac{\sum_{i=1}^{n}x_iy_i}{\sqrt{\sum_{i=1}^{n}x_i^2}\sqrt{\sum_{i=1}^{n}y_i^2}}$

余弦相似度计算是基于词袋模型的，在文本的向量表示中不会考虑词语之间的位置关系，因此余弦相似度模型理所当然地继承词袋模型的所有缺陷。对于如下两段文本，其意思完全相反，但两者余弦相似度为1：

这里的红富士很甜，但是水晶梨不好吃。
这里的水晶梨很甜，但是红富士不好吃。

余弦相似度不注重向量的模，而只注重向量的方向；相反，欧氏距离只注重向量的模，而不注重向量的方向。导致余弦相似度走向欧氏距离的另一个极端：很多常识上不相似的事物，余弦相似度结果非常高；很多常识上认为非常相似的事物，余弦相似度非常低。

汉明距离

在数据传输差错控制编码里，最常用的距离度量是汉明距离，它表示两个长度相同的字符串对应位置不同的字符的数量。汉明距离是以理查德·卫斯里·汉明（Richard Wesley Hamming）的名字命名，又译海明距离。在研究误差检测与校正码的基础性论文中首次引入的概念，其用于在通信中累计定长的二进制字符串中发生翻转的错误数据位，所以也被称为信号距离。

对于两个长度均为 $n$ 的字符串 $x$ 与 $y$ ，汉明距离计算公式： $dham(x,y)=∑i=1n(xi⊕yi)d_{ham}(x,y)=\sum_{i=1}^{n} (x_i \oplus y_i)$ ， $⊕\oplus$ 表示异或运算。

对于两个变量A与B，如果A与B的值相同，则有 $A⊕B=0A\oplus B=0$ ；如果A与B的值不相同，则有 $A⊕B=1A\oplus B=1$ 。

常用于信号处理，表明一个信号变成另一个信号需要的最小操作次数；实际就是比较两个比特串有多少个位的值不一样。简捷操作就是计算两个比特串在进行异或之后包含1的个数。也可用于图像处理领域比较二进制图像。

KL散度

Kullback-Leibler散度，衡量两个概率分布的匹配程度的指标。两个概率分布的差异越大，KL散度就越大；差异越小，KL散度就越小；当两个概率分布相同时，KL散度为0。

在实际应用中，对于某一个真实分布A，通过两个观察样本集，可得到两个不同的经验概率分布B和C。可使用KL散度判断两次抽样样本集哪一次更接近真实分布A。更常见的场景是有一个观察样本集，对应经验分布A，判断A与哪个理论分布（均匀分布、高斯分布、二次分布）更接近。

对于两个离散型随机变量P和Q，计算公式： $KL(P∣∣Q)=∑xp(x)logP(x)Q(x)KL(P||Q)=\sum_x p(x)log\frac{P(x)}{Q(x)}$
对于连续随机变量P和Q，计算公式： $KL(P∣∣Q)=∫(x)logP(x)Q(x)dxKL(P||Q)=\int (x)log\frac{P(x)}{Q(x)}dx$

海林格距离

Hellinger Distance，用于度量两个概率分布的相似度。对于离散型随机变量P和Q，其计算公式： $H(P,Q)=12∑i=1n(pi−qi)2H(P,Q)=\frac{1}{\sqrt2}\sqrt{\sum_{i=1}^n(\sqrt{p_i}-\sqrt{q_i})^2}$ 其中，分母 $2\sqrt2$ 是为了保证海林格距离小于或等于1，n为概率分布的可能取值数量。