数据结构 二叉树(1)
目录
1.链式结构表示二叉树
1.1 树结构定义函数
1.2 结点创建函数
1.3 树的构建函数
1.4 空指针NULL含义
1.链式结构表示二叉树
在前面的内容中,小编主要讲了关于二叉树中特殊的结构堆的实现。并且是使用顺序结构的数组
进行储存数据从而进行堆的实现的。而今天小编将介绍另一种实现二叉树的方式——链式结构实现
二叉树,即用链表来表示一个二叉树。
用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域
组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地
址,其结构如下:
1.1 树结构定义函数
typedef int BTDataType; //定义链式结构的二叉树 typedef struct BinaryTreeNode {BTDataType data; // 当前结点值struct BinaryTreeNode* left; // 指向当前结点左孩子struct BinaryTreeNode* right; // 指向当前结点右孩子 }BTNode;- 作用:用 typedef 定义二叉树结点的结构体 BTNode ,每个结点包含:
- 1 个数据域 data (类型为 BTDataType ,已通过 typedef 设为 int ),存储结点的值
。
- 2 个指针: left (指向左子树)、 right (指向右子树),体现二叉树的链式存储。
二叉树的创建方式比较复杂,为了更好的步入到二叉树内容中,我们先手动创建一棵链式二叉树:
1.2 结点创建函数
//创建相应的节点并初始化 BTNode* buyNode(char x) {BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){printf("malloc failed\n");return NULL;}node->data = x;node->left = node->right = NULL;return node; }- 作用:动态创建 1 个二叉树结点,为构建树做基础。
- 步骤:
1. 用 malloc 申请 BTNode 大小的内存,返回地址存到 node 。
2. 检查 malloc 是否失败(若失败, perror 打印错误,返回 NULL )。
3. 给新结点赋值: 将所要赋值的值赋值给 data 并将left 、 right 初始化为 NULL (表示无
左右子树 )。
4. 返回新结点地址 node ,供后续构建树时连接。
1.3 树的构建函数
BTNode* createBinaryTree() {BTNode* nodeA = buyNode('A');BTNode* nodeB = buyNode('B');BTNode* nodeC = buyNode('C');BTNode* nodeD = buyNode('D');BTNode* nodeE = buyNode('E');BTNode* nodeF = buyNode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->left = nodeE;nodeC->right = nodeF;return nodeA; //返回头结点}- 作用:手动构建一棵具体的二叉树,返回根结点( nodeA ),树的结构由指针连接决定。
- 步骤:
1. 调用 buyBTNode 创建 6 个结点( nodeA 到 nodeF ),值分别为 A~F 。
2. 通过指针赋值连接结点,构建树结构:
- nodeA 是根结点, nodeA->left = nodeB (根的左子树是 nodeB )、 nodeA->right =nodeC (根的右子树是 nodeC )。
- nodeB->left = nodeD ( nodeB 的左子树是 nodeD ); nodeC->left = nodeE 、 nodeC->right = nodeF ( nodeC 的左子树 nodeE 、右子树 nodeF )。
3. 返回根结点 nodeA ,调用 createBinaryTree就能拿到整棵树的入口,后续可基于根操作(如遍历)。
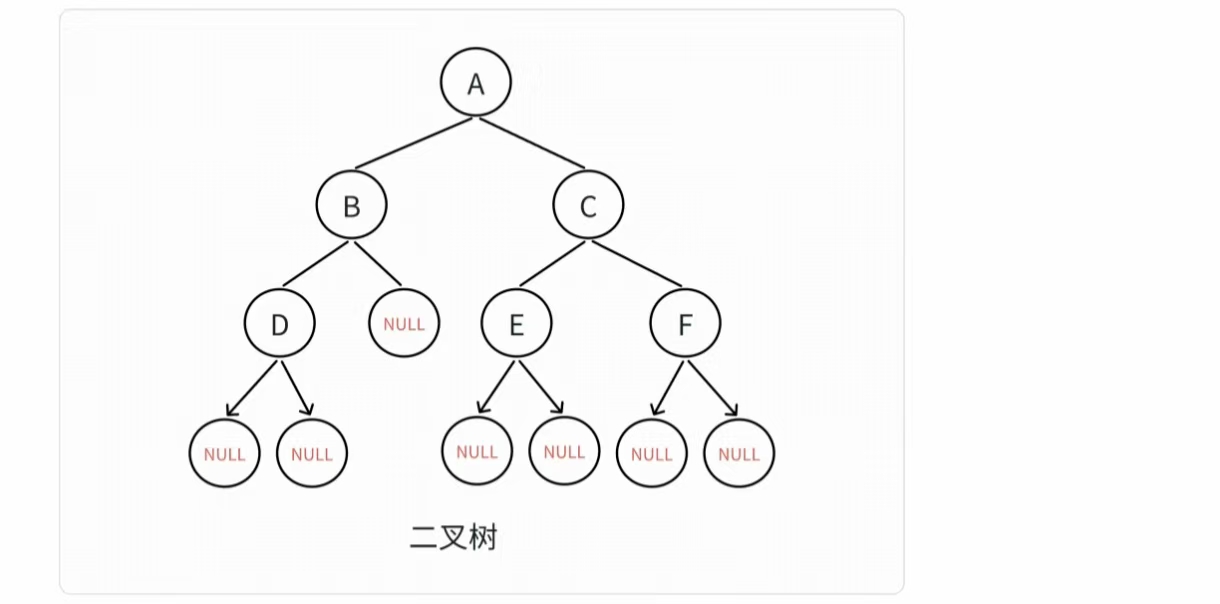
以上便是小编手动创建的一棵链式二叉树(用字母表示该结点的数据)。用图表示出来就是下面这个
图:
1.4 空指针NULL含义
最下面的空指针NULL在理解的时候可以忽略。图里的 NULL 表示空指针,代表二叉树中某个节点
没有左子树或右子树 。具体来说:二叉树的节点通过指针( left 、 right )指向子节点。如果节点
的 left 或 right 为 NULL ,就说明该方向没有子树(是空分支)。
比如:
- 节点 B 的右子树是 NULL → 表示 B 没有右孩子。
- 节点 D 的左、右子树都是 NULL → 表示 D 是叶子节点(没有子节点)。
还要注意的是 : NULL 在二叉树中是递归终止的标志,也是“空树”的表示:
- 遍历二叉树时(比如递归遍历),遇到 NULL 就知道“当前子树为空”,不需要继续递归。
- 构建二叉树时,用 NULL 初始化节点的 left / right ,表示“暂时没有子节点”,后续需要连接子树
时再赋值。这些小编在后面的递归遍历树中会强调的。大家只要记住 : NULL 是二叉树里“空分支”
的标志,告诉程序“这里没有子树了”。
回顾二叉树的概念,二叉树分为空树和非空二叉树,非空二叉树由根结点、根结点的左子树、根结
点的右子树组成的,下面再用数字举个简单的例子:
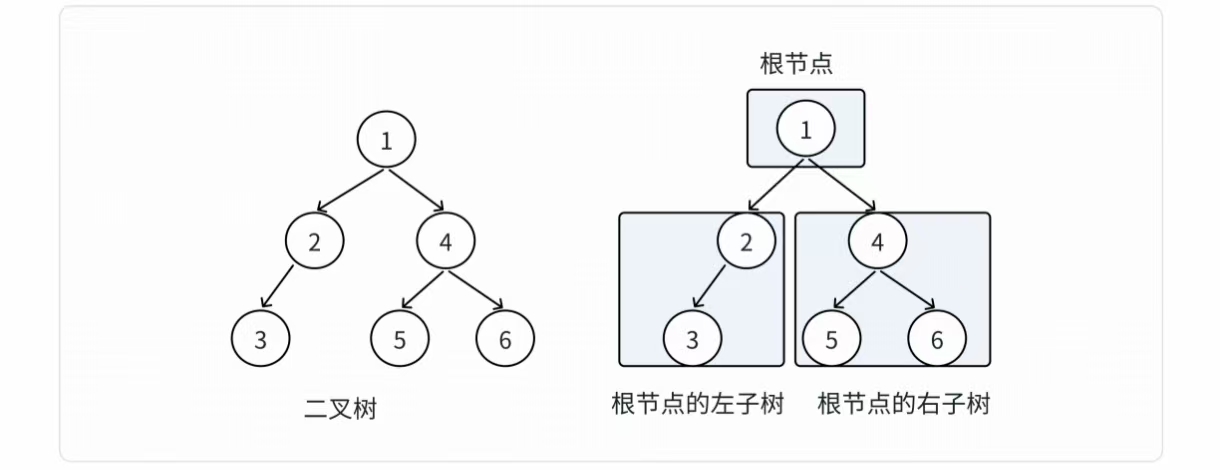
根结点的左子树和右子树分别又是由子树结点、子树结点的左子树、子树结点的右子树组成的,因
此二叉树定义是递归式的,后序链式二叉树的操作中基本都是按照该概念实现的。
以上便是用链式结构表示并实现二叉树的主要内容,当然后面还要涉及到二叉树的遍历以及各个结
点有关的查找,小编会在下一篇用链式结构实现二叉树中详细讲到。欲听后事如何,且听下回解。
最后感谢大家的观看!
