当前位置：首页 > backend >正文

机器学习笔记(三)——决策树、随机森林

backend 2025/7/27 9:36:42

写在前面：

写本系列(自用)的目的是回顾已经学过的知识、记录新学习的知识或是记录心得理解，方便自己以后快速复习，减少遗忘。概念部分大部分来自于机器学习菜鸟教程，公式部分也会参考机器学习书籍、阿里云天池。机器学习如果只啃概念始终学不牢，因此我打算概念与代码结合。

决策树部分来自于b站up主等等很简单，可以去看她的视频，讲的很不错。我在她的基础上补充了一些内容。

part 2 机器学习算法

三、决策树

决策树（Decision Tree）是一种常用的机器学习算法，广泛应用于分类和回归问题。

1、决策树的概念与用法

决策树的训练阶段是根据给定训练集构造出一棵树，测试阶段是根据构造出来的树模型从上到下走一遍，得到结果。因此一旦构建出决策树，后续的分类或预测任务就很简单了。

(1)引入

有一份数据，提供了每个人是否有房、婚姻状况、年收入以及是否是拖欠贷款者的信息。现在需要你根据这份数据，判断一个没有房、单身、年收入70k的人是否拖欠贷款。

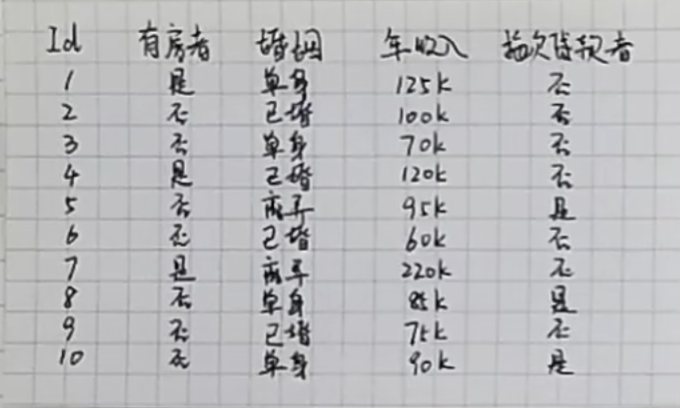
决策树可以用来解决这个问题。我们可以根据表中数据构建这样的决策树：

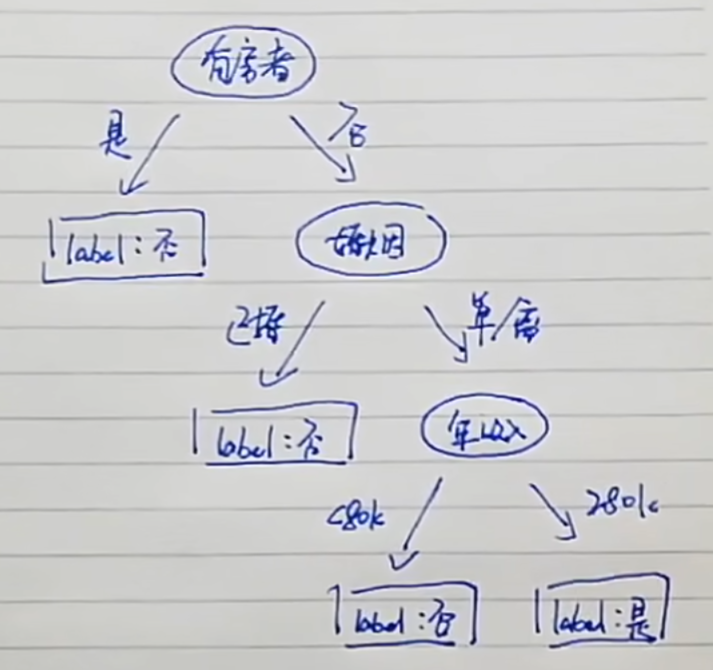
根据这颗决策树，如果一个人，没有房，单身，年收入＞80k，那么他就可能拖欠贷款。现在的问题就是，如何构建决策树呢。

(2)决策树的节点

先来看表中的属性，属性可以用来构建决策树的节点。表中共有三种属性：二元属性(是否有房)、多元属性(单身、已婚、离异)、序列属性(年收入)。

二元属性作为决策树节点很简单，只需要两个分支：

多元属性作为决策树节点，可以直接写多条分支，也可以将相近的分支合并：

序列属性作为决策树节点，我们可以根据经验或者根据数据进行推测，自己划分区间作为分支，在后面的节点选择顺序部分会说明怎么划分：

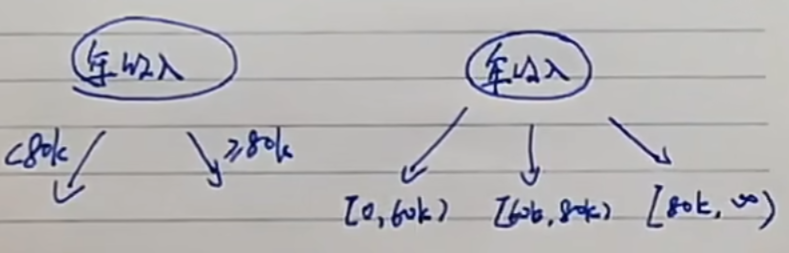
(3)节点的选择顺序

构建了节点后，就需要知道，哪个节点先使用(放在根部)，哪个节点放在第二层...

节点的顺序选择可以采用以下两种方式：

1、熵 $Entropy = -\sum_{i=1}^{n-1}p(i)log_2p(i)$

2、Gini系数 $1-\sum_{i=0}^{n-1}[p(i)]^2$

其中P(i)是指的是概率，后续计算会说明。

首先来介绍熵：熵是表示随机变量不确定性的度量，熵值越小，数据越纯越稳定。

Gini系数的取值在0~0.5之间，也是Gini系数的值越小，数据越纯越稳定。

我们分类或者是做回归时，肯定希望分类后得到的每个类别都比较纯，即类内之间相似度高，类间相似度低。

当我们选择某个属性来进行划分时，假设我们得到了划分1和划分2，划分1和划分2的Gini系数/熵值肯定是越小越好。计算出划分1和划分2的Gini系数/熵后我们再来计算Gini加权/熵的加权，也就是用划分1的概率(划分1占总体的比例)×划分1的Gini系数/熵值+划分2的概率×划分2的Gini系数/熵值。这样就得到了划分后“整体”的Gini系数/熵。通过比较用不同属性进行划分得到的Gini系数/熵，看谁的小(如果是熵的话就是谁的信息增益大)，就能够选出使Gini系数/熵最小的那个属性来作为先使用的节点。

其中，属性X(特征X)使得整体Y的不确定性减少的程度称为信息增益。例如，系统熵值从原始的0.88下降到了0.56，就可以说此时的信息增益为0.32。

这里没看懂的话可以先看后面构建决策树的实例，看明白例子后这段话就很好理解了。

另外，前面提到过，在遇到连续序列时，可以自己划分连续序列。在介绍完熵值和Gini系数后，就可以详细说一下如何划分了。我们可以遍历这个连续序列，每次都选择不同的地方进行划分，将划分的结果依次去计算熵/Gini系数，选择结果最小的那一次划分。这就是预剪枝。

(4)算法版本(可以跳过)

这里来说一下决策树算法的版本

1、ID3：信息增益(采用熵)

2、C4.5：信息增益率(解决ID3的问题)

3、CART：使用Gini系数，并且是二叉树，每次都将类型分为两类

这里说明一下ID3的不足。例如，如果还有一个属性(特征)是id值，那么对于每个个体而言，id值都是唯一的，也就是类别特别多的情况下，ID3很可能会过拟合，CART 对多类别特征的处理能力优于 ID3。除此之外，解决ID3不足的方式就是使用C4.5。

C4.5引入了信息增益率，信息增益率 = 信息增益/自身熵值。此时，当采用id值进行分类时，得到的数据很纯，信息增益的确很大，但此时自身的熵值更大，信息增益率反而小，就解决了ID3的问题。

(5)预剪枝和后剪枝(可以跳过)

为什么要剪枝呢？决策树过拟合的风险很大，因为从理论上来说，只要我们的树够大够深，就能把每个类完美地分开，但这会导致过拟合，因此就需要剪枝。

1、预剪枝。预剪枝体现在限制深度，叶子节点个数，叶子节点样本数，信息增益量等。比如限制深度为3，叶子节点个数为5。还可以限制叶子节点样本数为10，例如，当分裂到某一层时，该叶子节点只剩10个样本了，就不允许它继续分裂了。关于如何选择预剪枝方式，这需要在实验中进行不断观察和尝试。

2、后剪枝(用的不多)。这里介绍一下CART的后剪枝方法。建立完决策树后来进行剪枝，通过一定的衡量标准(损失值)：

$C_\alpha(T) = Gini*|T_{sample}|+\alpha|T_{leaf}|$

举个例子，看下面这棵树，我想确定一下红色框内的节点需不需要分裂：

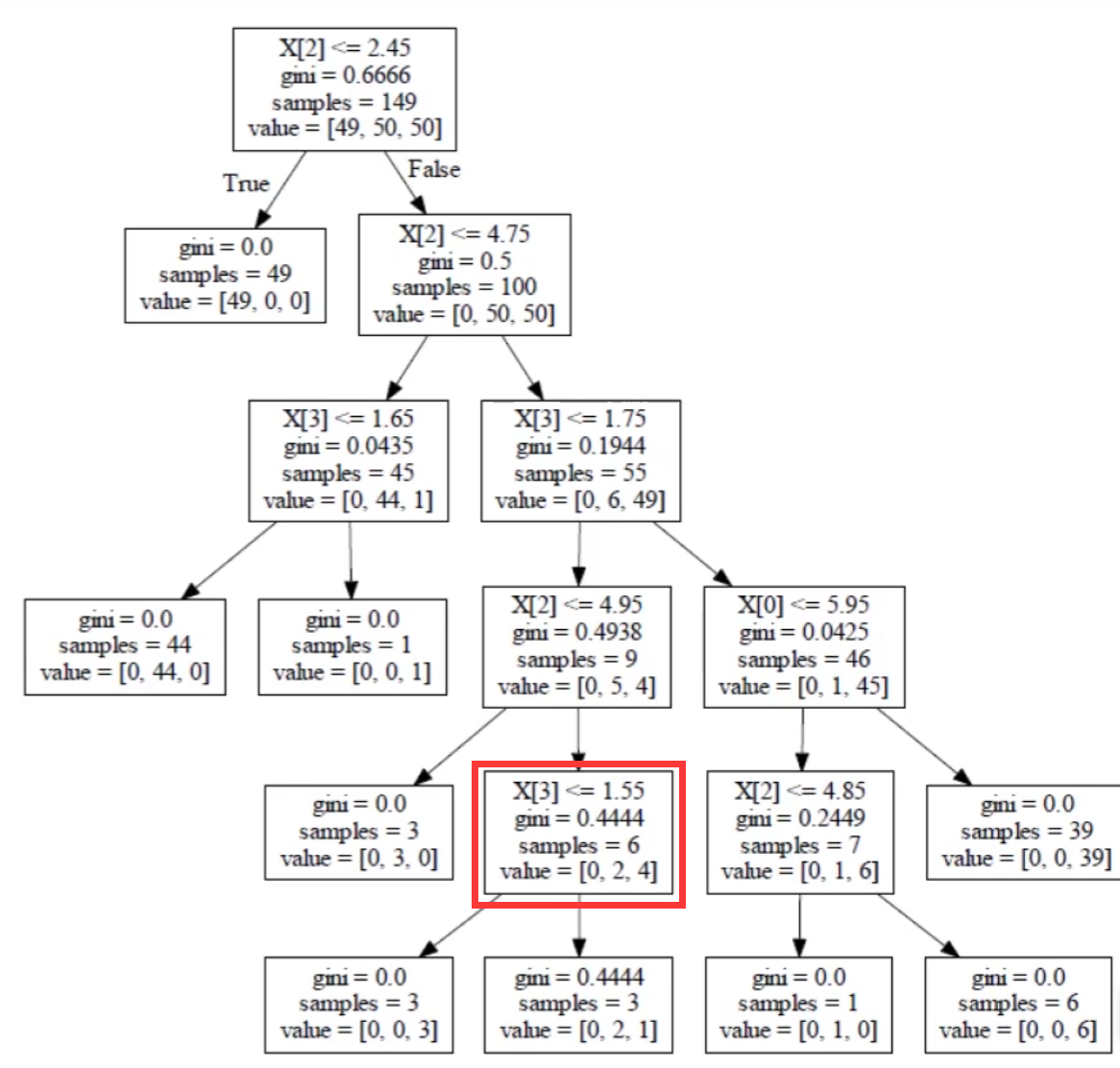
那么，如果不分裂的话，根据上面的公式，损失值就是：0.4444×6+1×α(1是因为不分裂的叶子节点只有它自己)

如果分裂的话，损失值是：0×3+0.4444×3+2×α

损失值越小越好，因此假如不分裂的损失值小，就选择不分裂。式中的α是我们规定的。

(6)构建决策树

这里以Gini系数为例构建决策树

从上面的分析我们知道，我们的目标是为了让数据划分后的Gini系数减小，现在我们来分别计算通过是否有房、婚姻情况、年收入对数据进行划分后，哪个方式划分得到的结果Gini系数最小：

1、有房者

这里对计算过程进行简单的解释：

首先，根据是否有房，可以将数据划分为两部分，即3个人有房，7个人无房，因此有房的概率为 $\frac{3}{10}$ ，无房的概率为 $\frac{7}{10}$ 。

对于有房的3个人而言，拖欠贷款的人数为0，没有拖欠贷款的人数为3。因此概率分别为0和1。现在计算有房的人的Gini系数，根据公式可求得0。

对于无房的7个人而言，拖欠贷款的人数为3，没有拖欠贷款的人数为5。因此概率分别为 $\frac{3}{7}$ 和 $\frac{4}{7}$ 。现在计算有房的人的Gini系数，根据公式可求得 $\frac{24}{49}$ 。

现在算划分后新的Gini系数，也就是Gini加权。Gini系数为0的有3个人，概率为 $\frac{3}{10}$ ；Gini系数为 $\frac{24}{49}$ 的有7个人，概率为 $\frac{7}{10}$ 。求得Gini加权为 $\frac{12}{35}$ 。

2、婚姻状况

3、收入

这样，我们就分别计算了使用三个属性进行划分的Gini加权，可以看出，使用婚姻状况来划分的Gini系数最小，因此，决策树的第一层应该使用婚姻状况：

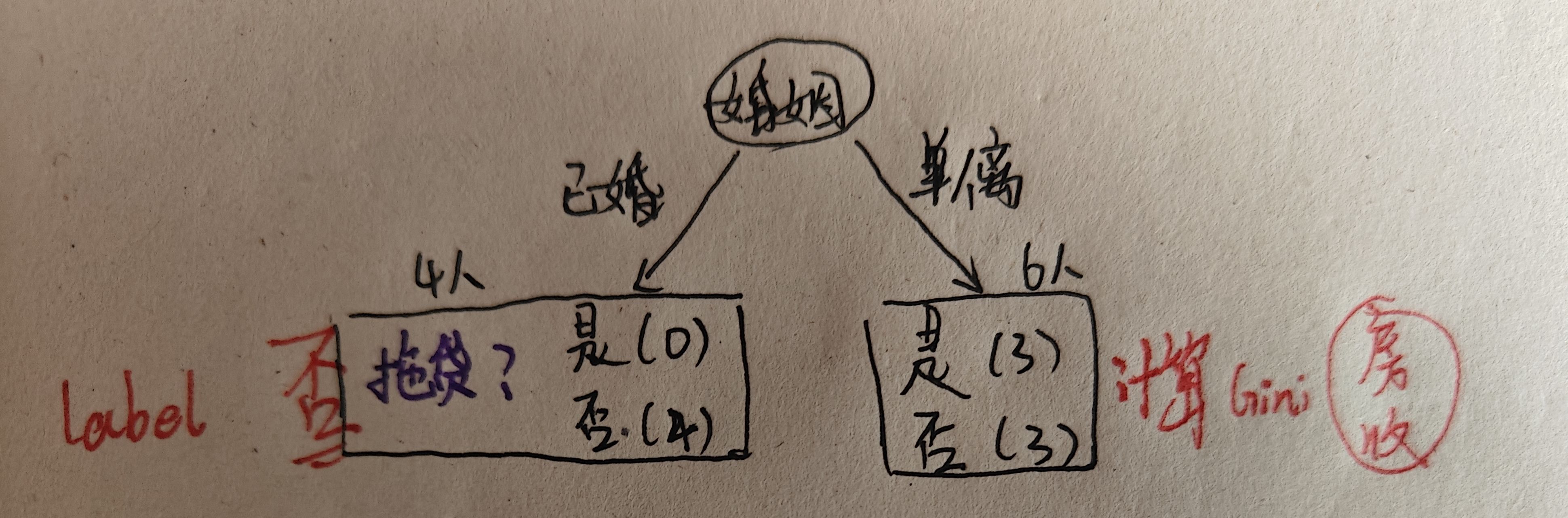
可以看出，已婚的4人都没有拖欠贷款，因此可以直接打上标签否。单身或离异的6人中，有三个人拖欠贷款，三个人不拖欠贷款，因此还需要通过剩下的两个属性将这六个人进行划分，降低Gini系数。现在我们可以选择的属性是是否有房和收入情况，现在重新计算Gini系数：

1、有房者

2、收入

有房者的Gini加权更小，因此第二个属性是有房者，可以继续构建决策树：

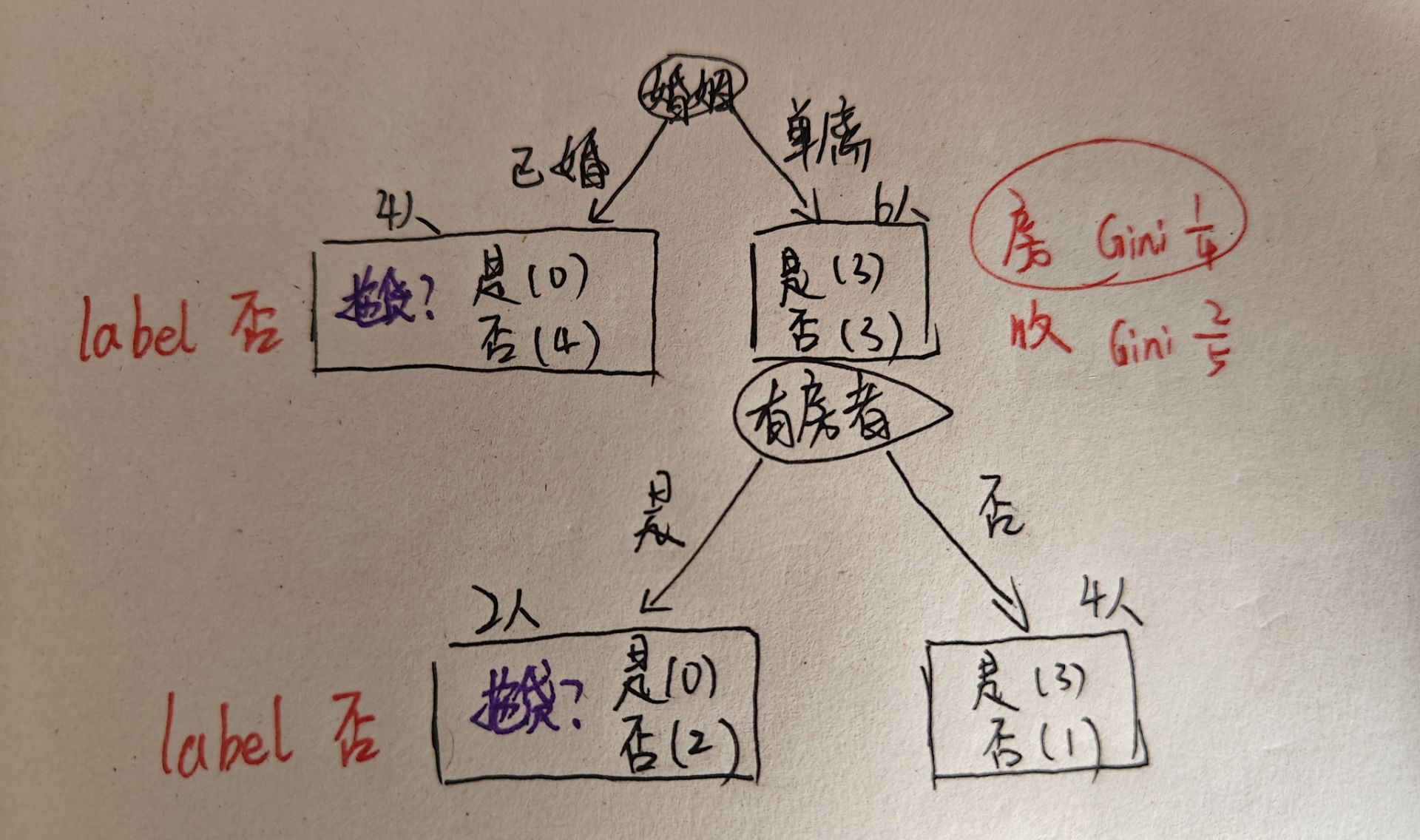
此时，有房的2人均未拖欠贷款，因此也可以打上否的标签。没有房的4个人有3个拖欠贷款，1个不拖欠贷款，因此还需要进一步判断。这里由于只剩下收入这一个属性，因此不需要再计算Gini系数。根据收入可以继续构建决策树：

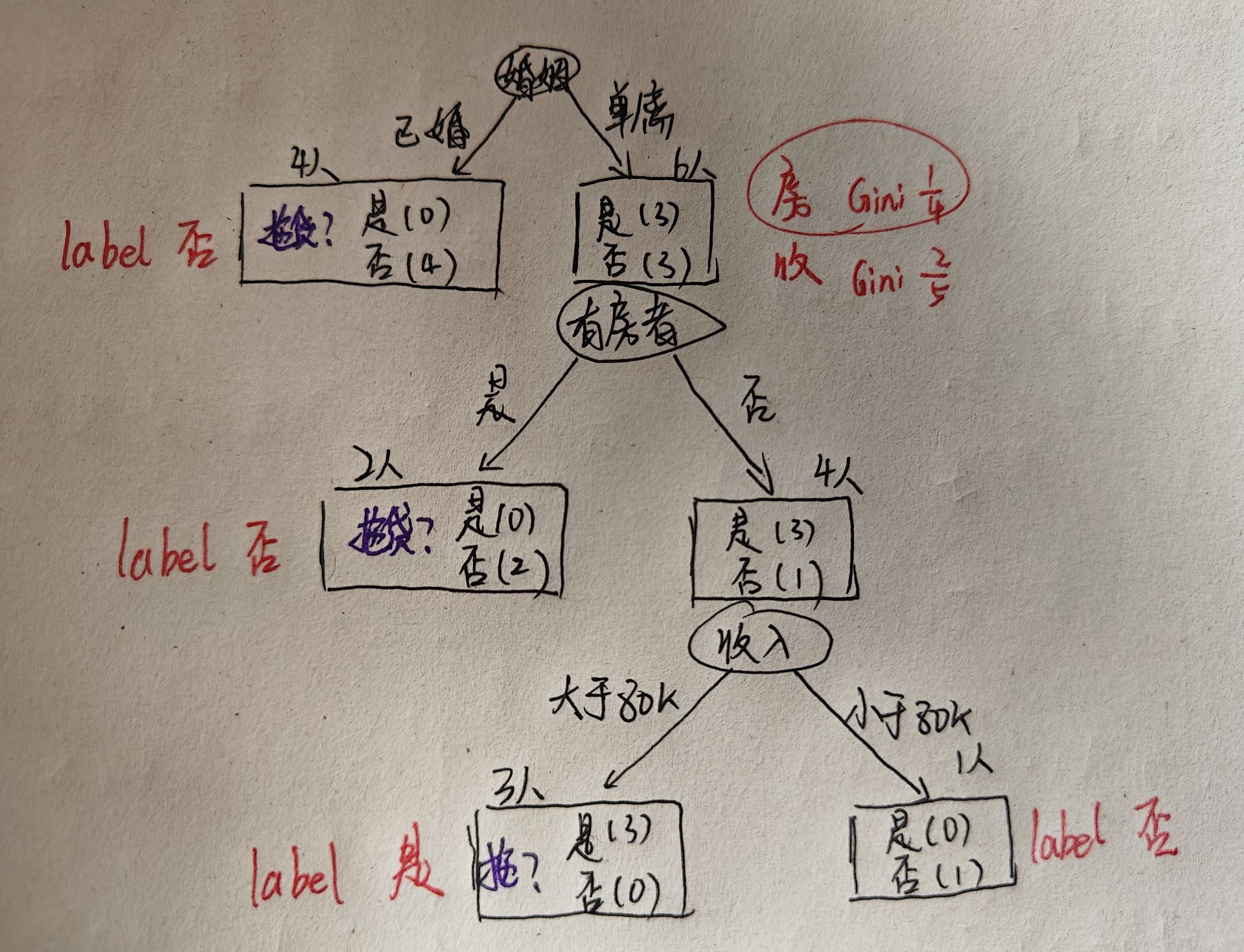
此时，收入大于80k的人均拖欠贷款，因此可以打上标签是，收入小于80k的人没有拖欠贷款，可以打上标签否。至此，决策树构建完毕。我们在一开始提到的没有房、单身、年收入70k的人，就可以根据这颗决策树判断为没有拖欠贷款。

(7)决策树进行回归任务

决策树在进行回归任务时，将衡量标准改为方差即可。

2、决策树的代码实现

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
'''
这里的X是特征矩阵，也叫自变量，y是标签向量，也叫因变量
test_size是测试集占总数据的比例，这里0.3就是设置为了30%
random_state = 42是随机数种子，确保划分结果一样，代码可复现
'''# 创建决策树分类器
clf = DecisionTreeClassifier()# 训练模型
clf.fit(X_train, y_train)# 对测试集进行预测
y_pred = clf.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.2f}")

四、随机森林

1、随机森林的概念

在学过决策树后，随机森林的思路就很简单了。随机森林的森林指的是多棵决策树，随机有两个方面的随机：

1、样本随机采样，比如第一棵树随机采用80%的样本之类

2、特征随机采样，比如有n个特征，颜色、大小、气味、纹路...等，第一棵树选择颜色、气味、纹路等，第二棵选择大小、气味等。

这样就可以保证每棵树得到的结果相似但不同，最后再对结果进行处理：

如果是回归任务，就对每棵树的结果取平均值

如果是分类任务，就对每棵树的结果取众数

这样就得到了最终结果。

随机森林的优点是：模型随机性强不容易过拟合、处理高维数据相对更快、树状结构，可解释度高。缺点是：模型往往不具备正确处理过于困难的样本的能力。

2、代码实现

# 导入必要的库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix# 加载数据集
iris = load_iris()
X = iris.data  # 特征
y = iris.target  # 标签# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 创建随机森林分类器
rf = RandomForestClassifier(n_estimators=100,         # 树的数量max_depth=None,           # 树的最大深度min_samples_split=2,      # 拆分内部节点所需的最小样本数min_samples_leaf=1,       # 叶子节点所需的最小样本数max_features='sqrt',      # 寻找最佳分割时要考虑的特征数量random_state=42,          # 随机种子，确保结果可复现n_jobs=-1                 # 使用所有CPU核心
)# 训练模型
rf.fit(X_train, y_train)# 在测试集上进行预测
y_pred = rf.predict(X_test)# 评估模型
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.2f}")# 查看分类报告（精确率、召回率、F1分数等）
print("\n分类报告:")
print(classification_report(y_test, y_pred, target_names=iris.target_names))

查看全文

http://www.xdnf.cn/news/16220.html