当前位置：首页 > backend >正文

相关类可视化图像总结

backend 2025/6/22 22:09:05

一、散点图（Scatter Plot）

1.定义

2.特点

3.变体

4.应用场景

5.Python代码实现

二、气泡图（Bubble Chart）

1.定义

2.特点

3.变体

4.应用场景

5.Python代码实现

三、相关系数矩阵

1.定义

2.特点

3.变体

4.应用场景

5.Python代码实现

四、平行坐标图（Parallel Coordinates Plot）

1.定义

2.特点

3.变体

4.应用场景

5.Python代码实现

五、二维密度图（2D Density Plot）

1.定义

2.特点

3.变体

4.应用场景

5.Python代码实现

六、桑葚图（Sankey Diagram）

1.定义

2.特点

3.变体

4.应用场景

5.Python代码实现

七、雷达图（Radar Chart）

1.定义

2.特点

3.变体

4.应用场景

5.Python代码实现

八、总结

一、散点图（Scatter Plot）

1.定义

散点图是一种二维数据可视化图表，通过将两个变量分别映射到横轴（X轴）和纵轴（Y轴），用点的位置表示数据点在两个变量上的取值，从而直观展示变量间的关系或分布模式。每个点代表一个观测样本，其核心是通过点的密集程度、分布趋势或异常位置，揭示变量间的“相关性”（如线性、非线性关系）、“聚类结构”或“离群值”。

2.特点

优势（Strengths）

直观展示双变量关系：无需复杂计算即可快速判断变量间是否存在关联（如正相关、负相关或无明显关联）。
易于识别异常值：远离集群的点可直接视为异常值，便于数据清洗或深入分析。
支持多变量扩展：通过颜色、大小、形状等视觉编码引入第三变量（如类别或数值），增强信息密度。

局限性（Limitations）

仅适用于二维数据：原生散点图无法直接展示三个以上变量，需结合分面、动画或其他高维可视化方法（如平行坐标图）。
仅能展示相关性，无法证明变量间的因果性（如冰淇淋销量与溺水率的相关性可能由第三方变量“气温”驱动）
当数据点数量极大时，点重叠会导致分布特征模糊，需配合透明度调整或二维密度图辅助展示。

3.变体

带颜色编码的散点图：用颜色区分数据类别（如不同物种、用户群体），适用于分组比较。
带大小编码的散点图：用点的大小表示第三数值变量，升级为三维信息展示（即“气泡图”）。
动态散点图：通过动画展示随时间变化的散点分布（如股票价格与交易量的动态关系。
分面散点图（Faceted Scatter Plot）：将数据按类别划分为多个子图（面），每个子图展示该类别下的双变量关系，适合对比分析。

4.应用场景

探索性数据分析（EDA）：分析变量间的相关性，辅助特征工程（如筛选有效特征）。案例：分析广告投入与销售额的关系，判断是否存在线性关联。
科学研究与工程：展示实验数据的分布规律（如化学反应中温度与产率的关系）。
质量控制与异常检测：在制造业中监控生产参数（如零件尺寸与公差），识别不合格产品。
地理信息可视化：用经纬度作为坐标，展示地理数据（如城市犯罪事件的分布与人口密度的关系）。

5.Python代码实现

import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
# 设置支持中文的字体，这里以 SimHei 为例，不同系统可能需要调整字体名称
plt.rcParams['font.family'] = 'SimHei'
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False
# 读取数据
crime = pd.read_csv("D:\\数据可视化\\(ch-5.2.1-2)crimeRatesByState2005.csv")# 设置图片清晰度
plt.rcParams['figure.dpi'] = 300# 设置中文字体
plt.rcParams['font.sans-serif'] = ['WenQuanYi Zen Hei']# 绘制散点图
sns.scatterplot(data=crime, x='murder', y='burglary', color='red')# 添加标题和轴标签
plt.title('谋杀案和入室盗窃案的散点图')
plt.xlabel('谋杀案数量')
plt.xticks(rotation=45)
plt.ylabel('入室盗窃案数量')# 显示图形
plt.show()

这段代码使用Python的seaborn和matplotlib库绘制了散点图，以展示美国各州谋杀案和入室盗窃案数量之间的关系。代码首先进行了中文显示的设置，解决了中文字体和负号显示的问题。随后读取了犯罪率数据集，并设置了图形的清晰度。通过seaborn的scatterplot函数，以红色点标记了每个州的谋杀案数量（x轴）和入室盗窃案数量（y轴）。最后添加了标题和轴标签，并旋转了x轴刻度以避免重叠。整体代码简洁有效，能够直观呈现两种犯罪案件数量之间的分布趋势，但可以进一步优化，如添加回归线以分析相关性、使用颜色区分不同地区或添加交互功能以显示州名等详细信息。

二、气泡图（Bubble Chart）

1.定义

气泡图是散点图的扩展形式，通过在二维坐标系（X 轴、Y 轴）的基础上，引入气泡的大小（半径或面积）作为第三变量，从而实现三变量数据的可视化。每个气泡代表一个数据点，其位置由两个数值型变量决定，大小则反映第三个数值型变量的量级。气泡图的核心是通过 “位置 + 大小” 的双重编码，直观展示三个变量之间的关联关系或分布模式。

2.特点

优势（Strengths）

多变量整合能力：一次性展示三个变量的关系，避免了多图表拼接的复杂性。例如，通过 X 轴（收入）、Y 轴（消费）、气泡大小（人口）分析不同地区的经济特征。
规模差异可视化：气泡大小对数值敏感，可清晰反映第三变量的量级差异（如城市 GDP 规模、企业市值）。
灵活的扩展空间：可进一步通过颜色引入第四变量（如类别、状态），或通过透明度表示第五变量（如数据置信度）。

局限性（Limitations）

气泡重叠问题：当数据点密集或气泡大小差异大时，小气泡易被大气泡遮挡，导致信息丢失（如人口少的城市数据被人口多的城市覆盖）。
尺寸感知误差：人类对面积的感知不如长度精准，可能导致对第三变量的误判（如气泡面积翻倍时，人眼易认为半径仅增加 50%）。
高维数据限制：超过四个变量时，视觉编码复杂度骤增，可读性显著下降，需结合其他高维可视化方法（如平行坐标图）。

3.变体

彩色气泡图（带颜色编码）：用颜色区分数据类别（如不同行业、产品类型），升级为四变量展示
3D 气泡图：通过三维坐标轴展示三个变量，气泡大小作为第四变量，但深度感知较弱，实际应用较少。
动态气泡图：结合时间维度，通过动画展示气泡位置、大小、颜色随时间的变化（如全球各国 GDP 增长趋势），需借助plotly或matplotlib.animation实现。
比例气泡图：气泡面积严格与第三变量成正比（面积 = k× 数值），而非半径，避免尺寸感知误差。

4.应用场景

市场与商业分析：分析产品竞争力（X 轴：用户评分，Y 轴：市场份额，气泡大小：销量）案例：电商平台分析商品的 “点击率 - 转化率 - 销量” 关系，定位高潜力商品。
地理与环境科学：展示区域数据（X/Y 轴：经纬度，气泡大小：污染指数，颜色：城市等级）。
教育与社会科学：研究学生表现（X 轴：学习时间，Y 轴：成绩，气泡大小：课外实践时长）。
金融与投资：分析股票特征（X 轴：市盈率，Y 轴：市净率，气泡大小：市值，颜色：行业）。

5.Python代码实现

import matplotlib.pyplot as plt
import numpy as np# 设置中文字体支持
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]# 创建非随机数据集 - 某电商平台不同品类商品分析数据
# 商品品类名称
categories = ['电子产品', '服装鞋帽', '食品饮料', '家居用品', '图书音像','美妆个护', '母婴用品', '运动户外', '宠物用品', '珠宝首饰']# X轴数据 - 平均月销量（万件）
x_values = np.array([12.5, 28.3, 42.7, 19.8, 8.6, 15.2, 22.9, 14.3, 9.7, 6.4])# Y轴数据 - 平均利润率（%）
y_values = np.array([28.5, 15.2, 8.3, 22.1, 35.4, 32.6, 18.7, 26.3, 30.1, 45.2])# 气泡大小 - 库存周转率（越高表示库存管理效率越高）
sizes = np.array([75, 62, 90, 68, 82, 78, 55, 70, 85, 48]) * 5  # 放大气泡尺寸以便显示# 气泡颜色 - 客户满意度评分（5分制）
colors = np.array([4.2, 3.8, 4.5, 3.9, 4.7, 4.1, 3.7, 4.3, 4.6, 4.0])# 创建气泡图
plt.figure(figsize=(12, 9))  # 设置图形大小# 使用scatter函数绘制气泡图
scatter = plt.scatter(x_values,y_values,s=sizes,        # 气泡大小c=colors,       # 气泡颜色alpha=0.7,      # 透明度cmap='plasma',  # 颜色映射表edgecolors='k', # 气泡边缘颜色linewidths=1    # 气泡边缘线宽
)# 添加颜色条
cbar = plt.colorbar(scatter)
cbar.set_label('客户满意度评分 (5分制)', fontsize=12)# 添加标题和轴标签
plt.title('电商商品品类分析气泡图', fontsize=18)
plt.xlabel('平均月销量 (万件)', fontsize=14)
plt.ylabel('平均利润率 (%)', fontsize=14)# 设置坐标轴范围
plt.xlim(0, 50)
plt.ylim(0, 50)# 添加网格线
plt.grid(True, linestyle='--', alpha=0.7)# 添加图例 - 气泡大小参考
for size in [100, 300, 500]:plt.scatter([], [], s=size, c='gray', alpha=0.6, edgecolors='k', linewidths=1,label=f'库存周转率: {int(size/5)}')plt.legend(title='气泡大小参考', loc='upper right', fontsize=10)# 为每个数据点添加标签
for i, category in enumerate(categories):plt.annotate(category,(x_values[i], y_values[i]),textcoords="offset points",xytext=(0, 10),ha='center',fontsize=10,bbox=dict(boxstyle="round,pad=0.3", fc="white", ec="gray", alpha=0.8))# 添加参考线 - 行业平均利润率和销量
plt.axhline(y=25, color='r', linestyle='--', alpha=0.5, label='行业平均利润率')
plt.axvline(x=20, color='g', linestyle='--', alpha=0.5, label='行业平均月销量')
plt.legend(loc='lower right')# 显示图形
plt.tight_layout()  # 自动调整布局
plt.show()

这段代码使用了一个电商平台不同品类商品的分析数据来绘制气泡图。数据包括：X 轴：平均月销量（万件），Y 轴：平均利润率（%），气泡大小：库存周转率（乘以 5 以放大显示效果），气泡颜色：客户满意度评分（5 分制）。图表中还添加了行业平均利润率和销量的参考线，以及每个品类的标签注释，便于直观分析不同品类商品的表现。

从气泡图分析可知，电商平台各品类商品表现差异显著。珠宝首饰利润率最高但销量最低，适合高净值客户策略；食品饮料销量最高但利润率低，需优化供应链；电子产品销量和利润率均高于行业平均，是核心盈利品类；母婴用品销量中等但库存周转率低，需改善库存管理；图书音像和宠物用品虽满意度高但销量低，可加大推广力度。整体来看，高满意度与高利润率无明显关联，库存周转率与销量也无直接关系，各品类需针对性调整经营策略。

三、相关系数矩阵

1.定义

相关系数矩阵是一个方阵，其中每个元素表示两个变量之间的相关程度。最常用的是 Pearson 相关系数，计算公式为：

其中，是变量 X 和 Y 的协方差，

和分别是 X 和 Y 的标准差。

2.特点

优点：

对称性：
范围：取值范围为 [-1, 1]
主对角线为 1：每个变量与自身完全相关
线性关系：Pearson 系数衡量的是线性相关程度

局限性

仅反映线性关系：对非线性关系不敏感
受异常值影响大：异常值可能扭曲相关系数
因果关系误判：相关性不等于因果性
分布依赖性：Pearson 系数要求变量服从正态分布

3.变体

Kendall 秩相关系数：基于数据秩次的非参数方法，对异常值不敏感
Spearman 秩相关系数：基于数据秩次的非参数方法，计算简单
距离相关系数：能够检测非线性关系
偏相关系数：控制其他变量影响下的两变量相关性

4.应用场景

金融领域：资产间相关性分析，投资组合优化
生物学：基因表达数据相关性分析
市场营销：客户特征与购买行为相关性分析
社会科学：变量间关系的量化研究
机器学习：特征选择，去除高度相关特征

5.Python代码实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns# 更简单的中文字体设置，使用系统常见的 SimSun（宋体），若系统无该字体可换其他
plt.rcParams["font.sans-serif"] = ["SimSun"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示为方块的问题# 创建非随机数据集 - 某电商平台不同品类商品分析数据
data = {'平均月销量(万件)': [12.5, 28.3, 42.7, 19.8, 8.6, 15.2, 22.9, 14.3, 9.7, 6.4],'平均利润率(%)': [28.5, 15.2, 8.3, 22.1, 35.4, 32.6, 18.7, 26.3, 30.1, 45.2],'库存周转率': [75, 62, 90, 68, 82, 78, 55, 70, 85, 48],'客户满意度评分(5分制)': [4.2, 3.8, 4.5, 3.9, 4.7, 4.1, 3.7, 4.3, 4.6, 4.0],'客单价(元)': [1250, 480, 85, 320, 65, 280, 240, 380, 120, 1500],'广告投入(万元)': [35, 62, 28, 42, 18, 32, 25, 30, 15, 45]
}
categories = ['电子产品', '服装鞋帽', '食品饮料', '家居用品', '图书音像','美妆个护', '母婴用品', '运动户外', '宠物用品', '珠宝首饰']
df = pd.DataFrame(data, index=categories)# 计算三种相关系数矩阵
correlation_matrix = df.corr()  # Pearson
spearman_matrix = df.corr(method='spearman')  # Spearman 秩相关# 创建画布
plt.figure(figsize=(18, 15))# 绘制 Pearson 相关系数热力图
plt.subplot(2, 2, 1)
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', square=True,annot_kws={'size': 10}, vmin=-1, vmax=1)
plt.title('Pearson 相关系数矩阵热力图', fontsize=14)# 绘制 Spearman 秩相关系数热力图
plt.subplot(2, 2, 3)
sns.heatmap(spearman_matrix, annot=True, cmap='coolwarm', square=True,annot_kws={'size': 10}, vmin=-1, vmax=1)
plt.title('Spearman 秩相关系数矩阵热力图', fontsize=14)# 绘制散点图矩阵
plt.subplot(2, 2, 4)
pd.plotting.scatter_matrix(df, alpha=0.8, figsize=(10, 10), diagonal='kde')
plt.suptitle('变量间散点图矩阵', fontsize=14)plt.tight_layout()
plt.show()# 打印相关系数矩阵
print("Pearson 相关系数矩阵:\n")
print(correlation_matrix.round(2))
print("\nSpearman 秩相关系数矩阵:\n")
print(spearman_matrix.round(2))

上述代码中，创建包含 6 个业务指标的 10 品类数据集，涵盖销量、利润、库存、满意度等关键维度。计算两种相关系数矩阵：Pearson：衡量线性相关，Spearman：基于秩次的非线性相关。可视化展示：使用 seaborn 热力图展示两种相关系数矩阵，通过 pandas 散点图矩阵直观呈现变量间关系，支持中文字体显示（配置 SimSun 字体）。结果打印两种相关系数矩阵的数值结果，保留两位小数。

四、平行坐标图（Parallel Coordinates Plot）

1.定义

平行坐标图是一种可视化高维数据的图表技术，它将每个数据维度用一条垂直的坐标轴表示，所有坐标轴平行排列。每个数据点通过连接各坐标轴上对应值的折线来表示。这种图表允许用户在二维平面上同时展示和比较多个维度的数据。

2.特点

优点

高维数据可视化：能够同时展示和比较 3 个或更多维度的数据，突破了传统二维图表的限制。
模式识别：通过观察折线的形状和相对位置，用户可以快速识别数据中的模式、聚类和异常值。
交互性强：在交互式可视化工具中，用户可以重新排列坐标轴、刷选特定范围的数据，或突出显示特定的数据点。
直观比较：易于比较多个数据点在不同维度上的相对值。

局限性

坐标轴顺序敏感：坐标轴的排列顺序可能影响用户对数据的理解和模式识别。
高密度数据混乱：当数据点数量较多时，折线可能相互重叠，导致视觉混乱，难以解读。
非对称感知：人类视觉系统在判断平行线之间的关系时比判断斜线更准确，这可能影响对某些数据模式的感知。
异常值影响：极端值可能扭曲整体视图，掩盖其他数据点的模式。

3.变体

聚类平行坐标图：将相似的数据点分组或着色，增强对聚类的识别。
时间平行坐标图：用于展示随时间变化的多维数据，其中一个坐标轴通常表示时间。
堆叠平行坐标图：通过堆叠折线或使用不同透明度来处理高密度数据。
径向平行坐标图：将坐标轴排列成放射状，从中心点向外发散，适用于展示周期性数据。
条件平行坐标图：根据特定条件或分组变量分割数据，创建多个平行坐标子图。

4.应用场景

金融分析：比较不同股票或投资组合在多个指标（如收益率、风险、市值等）上的表现。
医疗研究：分析患者在多个生理指标（如血压、血糖、心率等）上的健康数据。
市场调研：可视化消费者在多个维度（如价格敏感度、品牌忠诚度、使用频率等）上的行为数据。
工程优化：在多个性能指标下比较不同设计方案或参数组合。
数据挖掘：作为探索性数据分析工具，帮助识别高维数据中的模式和异常。

5.Python代码实现

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import StandardScaler# 设置中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题# 从网上下载鸢尾花数据集
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
column_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'class']
iris_data = pd.read_csv(url, header=None, names=column_names)# 数据预处理
# 标准化数值特征，使不同特征具有可比性
numeric_features = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
scaler = StandardScaler()
iris_data[numeric_features] = scaler.fit_transform(iris_data[numeric_features])# 创建平行坐标图
plt.figure(figsize=(12, 8))# 为不同类别设置不同颜色
colors = {'Iris-setosa': 'red', 'Iris-versicolor': 'green', 'Iris-virginica': 'blue'}# 绘制每个数据点的折线
for _, row in iris_data.iterrows():plt.plot(numeric_features, row[numeric_features],color=colors[row['class']], alpha=0.5, linewidth=1.5)# 添加标题和标签
plt.title('鸢尾花数据集的平行坐标图')
plt.xticks(rotation=45)
plt.xlabel('特征')
plt.ylabel('标准化值')# 添加图例
handles = [plt.Line2D([0], [0], color=color, label=label)for label, color in colors.items()]
plt.legend(handles=handles, title='鸢尾花类别')# 调整布局
plt.tight_layout()# 显示图形
plt.show()

这个代码示例实现了以下功能：数据获取：从 UCI 机器学习库下载经典的鸢尾花数据集，该数据集包含 4 个特征和 3 个类别。数据预处理：对数值特征进行标准化处理，确保不同特征在平行坐标图中具有可比性。可视化：使用 matplotlib 创建平行坐标图，为不同类别的鸢尾花设置不同颜色，便于区分。美观性：添加标题、标签和图例，并调整布局以确保图形清晰易读。

五、二维密度图（2D Density Plot）

1.定义

二维密度图（2D Density Plot），也称为密度热图或核密度估计图，是一种用于可视化二维数据分布的统计图形。它通过估计数据点在二维空间中的概率密度函数 (PDF)，用颜色或等高线来表示密度的高低。这种可视化方法特别适用于展示数据点的聚集模式、分布形状以及变量之间的关系。

2.特点

优点

平滑表示：使用核密度估计 (KDE) 等方法对离散数据点进行平滑处理，得到连续的密度分布。
直观展示分布：通过颜色深浅或等高线清晰展示数据在二维空间中的聚集区域和稀疏区域。
处理高密度数据：有效处理大量数据点的情况，避免散点图中常见的点重叠问题。
揭示数据结构：能够展示单峰、多峰分布以及变量间的相关性结构。
多种可视化方式：可以用填充颜色 (密度热图)、等高线或两者结合的方式呈现。

局限性

参数敏感性：核密度估计的结果高度依赖于带宽 (bandwidth) 参数，不同带宽可能导致不同的视觉解读。
计算复杂度：对于大规模数据集，核密度估计的计算成本较高。
信息损失：平滑处理可能掩盖数据中的局部细节或异常值。
解释歧义：密度图中的 "峰" 可能是数据真实聚集造成的，也可能是参数选择的结果。
维度限制：主要适用于二维数据，扩展到更高维度时可视化变得困难。

3.变体

等高线密度图：使用等高线表示密度分布，类似于地形图，适合展示分布的轮廓。
填充密度图：用连续的颜色填充表示密度，颜色越浓表示密度越高。
带散点的密度图：在密度图上叠加原始数据点，同时展示整体分布和具体数据位置。
二维直方图：将二维空间划分为网格，用网格中的计数表示密度，是一种离散化的密度估计。
三维密度图：将密度作为高度绘制为三维表面，提供更直观的空间感知。
条件密度图：根据第三个变量对数据分组，绘制多个条件密度图。

4.应用场景

地理学与环境科学：分析人口密度分布、污染物浓度空间分布等。
金融与经济学：研究资产价格与交易量的关系、不同经济指标的联合分布。
生物信息学：可视化基因表达数据、蛋白质结构中的原子分布。
用户体验研究：分析用户在界面上的点击热区分布。
天体物理学：展示星系在空间中的分布模式。
机器学习：可视化高维数据降维后的分布 (如 PCA、t-SNE 结果)。

5.Python代码实现

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats# 设置中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题# 从网上下载汽车MPG数据集
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data"
column_names = ['mpg', 'cylinders', 'displacement', 'horsepower', 'weight','acceleration', 'model_year', 'origin', 'car_name']
auto_data = pd.read_csv(url, header=None, names=column_names, na_values='?', sep='\s+')# 数据预处理
auto_data = auto_data.dropna()# 创建画布和子图
fig, axes = plt.subplots(2, 2, figsize=(14, 12))
fig.suptitle('汽车MPG数据集的二维密度图分析', fontsize=16)# 定义一个函数来使用scipy计算并绘制KDE
def plot_kde(x, y, ax, cmap='viridis', fill=True, thresh=0.05):# 计算二维核密度估计xmin, xmax = x.min(), x.max()ymin, ymax = y.min(), y.max()X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]positions = np.vstack([X.ravel(), Y.ravel()])values = np.vstack([x, y])kernel = stats.gaussian_kde(values)Z = np.reshape(kernel(positions).T, X.shape)# 标准化密度值以便设置阈值Z_norm = Z / Z.max()# 绘制KDE图if fill:contour = ax.contourf(X, Y, Z_norm, levels=np.linspace(thresh, 1, 20), cmap=cmap)fig.colorbar(contour, ax=ax)else:contour = ax.contour(X, Y, Z_norm, levels=np.linspace(thresh, 1, 10), cmap=cmap)fig.colorbar(contour, ax=ax)return ax# 1. 重量 vs 燃油效率
plot_kde(auto_data['weight'], auto_data['mpg'], axes[0, 0], cmap='viridis')
axes[0, 0].set_xlabel('汽车重量 (lbs)')
axes[0, 0].set_ylabel('燃油效率 (MPG)')
axes[0, 0].set_title('重量 vs 燃油效率的密度图')# 2. 马力 vs 加速度
plot_kde(auto_data['horsepower'], auto_data['acceleration'], axes[0, 1], cmap='Blues')
axes[0, 1].set_xlabel('马力')
axes[0, 1].set_ylabel('加速度 (0-60 mph 时间)')
axes[0, 1].set_title('马力 vs 加速度的密度图')# 3. 排量 vs 燃油效率 (带散点)
plot_kde(auto_data['displacement'], auto_data['mpg'], axes[1, 0], cmap='Reds')
axes[1, 0].scatter(auto_data['displacement'], auto_data['mpg'], alpha=0.3, s=10, color='black')
axes[1, 0].set_xlabel('排量 (立方英寸)')
axes[1, 0].set_ylabel('燃油效率 (MPG)')
axes[1, 0].set_title('排量 vs 燃油效率的密度图(带原始数据点)')# 4. 使用hexbin绘制二维直方图密度图
axes[1, 1].hexbin(auto_data['weight'], auto_data['horsepower'],gridsize=30, cmap='Purples', mincnt=1)
axes[1, 1].set_xlabel('汽车重量 (lbs)')
axes[1, 1].set_ylabel('马力')
axes[1, 1].set_title('重量 vs 马力的六边形密度图')
cb = fig.colorbar(axes[1, 1].collections[0], ax=axes[1, 1])
cb.set_label('数据点数量')# 调整布局
plt.tight_layout(rect=[0, 0, 1, 0.96])  # 为suptitle留出空间
plt.show()

上述代码用于可视化汽车 MPG 数据集的二维密度分布，主要流程为：

数据获取与预处理：从 UCI 数据库读取汽车数据，处理缺失值后保留有效样本。自定义密度图函数：使用 SciPy 的核密度估计（KDE）计算二维数据分布，通过contourf绘制填充等高线密度图，支持颜色映射和阈值设置，并添加颜色条辅助解读。

多子图可视化：左上子图展示汽车重量与燃油效率的密度分布，揭示负相关趋势；右上子图分析马力与加速度的关系，通过蓝色调密度热图呈现聚集模式；左下子图叠加散点与密度图，直观展示排量与燃油效率的分布及原始数据点位置；右下子图使用六边形分箱（hexbin）可视化重量与马力的二维直方图，通过紫色调映射数据点数量。

细节优化：设置中文字体、调整子图布局、添加坐标轴标签和标题，提升图形可读性。代码通过纯 Matplotlib 和 SciPy 实现，避免了 Seaborn 版本兼容性问题，有效展示了多组变量间的分布特征与潜在关联。

六、桑葚图（Sankey Diagram）

1.定义

桑葚图，也称为桑基图或能量流向图，是一种可视化技术，用于展示从一个集合到另一个集合的流程或转移关系。它由节点（通常表示实体或类别）和连接节点的流向线（表示转移关系）组成。流向线的宽度与流量大小成正比，因此可以直观地展示各节点间流量的相对大小和比例关系。

2.特点

优点

直观展示流量关系：通过流向线的宽度和颜色，清晰展示不同实体间的流量大小和方向。
层次结构清晰：适合展示具有层次结构的数据，例如能源转换、供应链或资金流动。
数据比例可视化：流向线的宽度与流量成正比，使读者能够直观感知各部分的相对重要性。
多维度展示：可以同时展示多个层级的节点和流向，适合复杂系统的可视化。
交互性强：在交互式版本中，可以悬停查看具体数值，点击节点或流向进行筛选。

局限性

节点布局复杂：对于节点数量较多或关系复杂的数据集，自动布局可能导致流向线交叉，降低可读性。
方向限制：传统桑葚图通常从左到右布局，可能不适用于所有类型的关系展示。
信息过载风险：过多的节点和流向可能使图表变得混乱，难以理解。
精确数值难以读取：虽然流向线宽度表示数量，但精确数值需要通过标签或交互方式获取。
时间动态展示困难：静态桑葚图难以有效展示随时间变化的流量关系。

3.变体

循环桑葚图：允许流向线形成闭环，用于展示循环系统，如生态系统或回收流程。
时间桑葚图：在时间轴上展示流量变化，例如不同时间段的能源消耗模式。
分层桑葚图：将节点按层级分组，使关系更加清晰，适合复杂的层次结构。
径向桑葚图：节点分布在圆周上，流向线从中心向外辐射，用于展示中心化的流量关系。
动态桑葚图：通过动画展示流量随时间的变化，增强对过程的理解。
交互桑葚图：允许用户通过点击或悬停探索数据细节，过滤特定节点或流向。

4.应用场景

能源分析：展示能源从生产到消费的整个生命周期，包括转换损失和最终用途。
供应链管理：可视化产品从原材料到最终消费者的流动路径和中间环节。
金融流动：分析资金在不同部门、机构或市场之间的流动，如国际贸易或投资。
教育与职业路径：展示学生从不同专业到就业领域的流向，或职业转换路径。
生态系统研究：模拟物质和能量在生态系统中的流动，如碳循环或食物链。
网络流量分析：展示数据在网络中的传输路径和带宽使用情况。
用户行为分析：分析网站或应用中用户的导航路径和转化漏斗。

5.Python代码实现

import pandas as pd
import plotly.graph_objects as go
import io
import requests# 尝试从URL获取数据，失败时使用本地备份数据
try:print("正在从远程获取能源数据...")url = "https://raw.githubusercontent.com/plotly/datasets/master/energy.csv"response = requests.get(url, verify=False)  # 临时禁用SSL验证response.raise_for_status()  # 检查请求是否成功energy_data = pd.read_csv(io.StringIO(response.text))print("数据获取成功！")
except Exception as e:print(f"无法从远程获取数据: {e}")print("使用内置备份数据...")# 备份数据 - 能源流动示例数据data = {'source': ['Primary Energy', 'Primary Energy', 'Primary Energy', 'Electricity Generation','Electricity Generation', 'Gas Network', 'Oil Refining'],'target': ['Electricity Generation', 'Gas Network', 'Oil Refining', 'Transmission & Distribution','Heat Generation', 'Final Consumers', 'Final Consumers'],'value': [100, 150, 80, 70, 30, 120, 75]}energy_data = pd.DataFrame(data)# 数据预处理
sources = energy_data['source']
targets = energy_data['target']
values = energy_data['value']# 创建节点标签列表
all_nodes = list(set(sources).union(set(targets)))# 创建节点索引映射
node_dict = {node: index for index, node in enumerate(all_nodes)}# 将源和目标转换为对应的索引
source_indices = [node_dict[source] for source in sources]
target_indices = [node_dict[target] for target in targets]# 创建颜色列表
colors = []
for i, source in enumerate(sources):current_source_index = source_indices[i]# 查找当前源索引在source_indices中的所有位置indices = [j for j, x in enumerate(source_indices) if x == current_source_index]# 获取对应的目标索引target_index = target_indices[indices[0]] if indices else 0target_val = all_nodes[target_index]if 'Electricity' in source or 'Electricity' in target_val:colors.append('#1f77b4')  # 蓝色表示电力elif 'Gas' in source or 'Gas' in target_val:colors.append('#ff7f0e')  # 橙色表示天然气elif 'Oil' in source or 'Oil' in target_val:colors.append('#2ca02c')  # 绿色表示石油elif 'Coal' in source or 'Coal' in target_val:colors.append('#d62728')  # 红色表示煤炭elif 'Renewable' in source or 'Renewable' in target_val:colors.append('#9467bd')  # 紫色表示可再生能源else:colors.append('#8c564b')  # 棕色表示其他能源# 创建桑葚图
fig = go.Figure(data=[go.Sankey(node=dict(pad=15,thickness=20,line=dict(color="black", width=0.5),label=all_nodes,color=['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728', '#9467bd','#8c564b', '#e377c2', '#7f7f7f', '#bcbd22', '#17becf']),link=dict(source=source_indices,target=target_indices,value=values,color=colors,hovertemplate='%{source.label} → %{target.label}<br>流量: %{value} TWh<extra></extra>')
)])# 设置标题和布局
fig.update_layout(title_text="2019年英国能源流动桑葚图",font_size=12,height=700,width=1000,hoverlabel=dict(bgcolor="white",font_size=12,font_family="Arial")
)# 显示图形
fig.show()# 如果需要保存为HTML文件以便在浏览器中查看
# fig.write_html("energy_sankey.html")

这段代码使用 Python 的 Plotly 库创建了一个展示 2019 年英国能源流动的桑基图。它先尝试从远程获取能源数据，失败则使用内置备份数据。数据预处理阶段将源和目标节点映射为索引，并为不同能源类型分配特定颜色。通过 `go.Sankey` 创建桑基图，设置节点和链接的样式，包括颜色、厚度等，链接的悬停模板显示能源流动信息。最后设置图表标题、尺寸等布局参数并展示，也可保存为 HTML 文件。

七、雷达图（Radar Chart）

1.定义

雷达图（Radar Chart），也称为蜘蛛图（Spider Chart）、星图（Star Plot）或极坐标图（Polar Chart），是一种可视化多维数据的图表类型。它将多个变量（维度）以从中心点辐射出的坐标轴表示，每个变量对应一个坐标轴，所有坐标轴具有相同的原点。数据点在每个坐标轴上的值用距离中心点的位置表示，最后将各个坐标轴上的点连接形成一个闭合多边形。

2.特点

优点

多维数据可视化：能够同时展示 3 个或更多维度的数据，突破了传统二维图表的限制。
直观比较：通过多边形的形状和面积，用户可以直观地比较不同数据点在多个维度上的表现。
对称性展示：所有维度共享同一个中心点，便于观察数据在各个维度上的平衡性。
模式识别：容易识别数据中的优势维度（离中心远的点）和劣势维度（离中心近的点）。
相对比较：适合展示相对数据，例如不同产品在多个指标上的评分比较。

局限性

维度数量限制：当维度数量过多时（超过 6-8 个），坐标轴会变得拥挤，图形可读性下降。
刻度敏感性：坐标轴刻度范围的选择会显著影响图形的视觉效果，可能导致误解。
面积错觉：多边形的面积并不总是与数据的实际总和成比例，可能导致对数据大小的误判。
数据重叠问题：当多个数据系列同时展示时，多边形可能相互重叠，影响可读性。
非等距感知：人类视觉系统对角度和弧度的感知不如对直线距离敏感，可能影响对数据的准确判断。

3.变体

填充雷达图：将多边形内部填充颜色，增强视觉效果，便于比较多个数据系列。
径向网格雷达图：使用径向网格线代替传统的圆形网格线，使数据点的位置更加清晰。
极坐标雷达图：使用连续的极坐标系统，适合展示周期性数据。
多层雷达图：将不同数据系列按层级展示，减少重叠问题。
交互式雷达图：支持悬停查看具体数值、点击筛选数据系列等交互功能。
堆叠雷达图：类似于堆叠柱状图，展示各维度的累积贡献。

4.应用场景

产品评估：比较不同产品在多个性能指标上的表现，如手机在处理器速度、电池续航、相机质量等方面的评分。
市场调研：分析消费者对品牌在多个维度上的认知，如价格、质量、服务、品牌形象等。
教育评估：评估学生在多个学科或技能领域的表现，如数学、语文、艺术、体育等。
企业竞争力分析：比较企业在市场份额、利润率、创新能力、员工满意度等多个方面的表现。
体育分析：展示运动员在不同能力指标上的优势和劣势，如足球运动员的速度、传球、射门、防守等能力。
游戏角色属性：在游戏中展示角色在力量、敏捷、智力、耐力等多个属性上的数值。
环境科学：比较不同地区在多个环境指标上的表现，如空气质量、水质、绿化率等。

5.Python代码实现

import pandas as pd
from pyecharts import options as opts
from pyecharts.charts import Radar# 加载数据
data = pd.read_csv('hot-dog-places.csv')# 提取年份和数据
years = data.columns.tolist()
values1 = data.iloc[0].tolist()
values2 = data.iloc[1].tolist()
values3 = data.iloc[2].tolist()# 配置雷达图的指标
c_schema = [{"name": year, "max": max(values1[i], values2[i], values3[i]) + 10} for i, year in enumerate(years)]# 创建雷达图
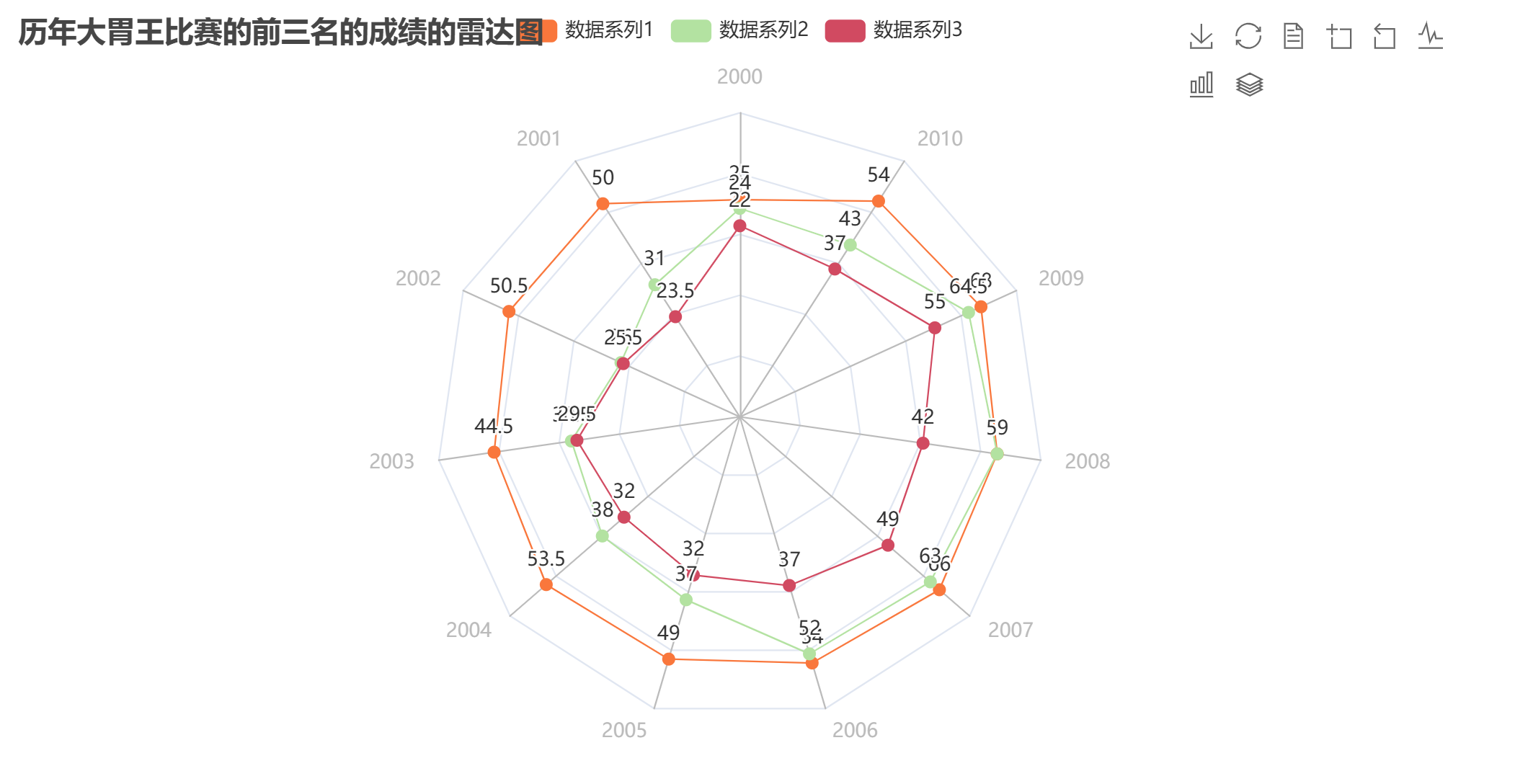
radar = (Radar().add_schema(schema=c_schema).add("数据系列1", [values1], color="#f9773c").add("数据系列2", [values2], color="#b3e2a1").add("数据系列3", [values3], color="#d14a61").set_global_opts(title_opts=opts.TitleOpts(title="历年大胃王比赛的前三名的成绩的雷达图"),legend_opts=opts.LegendOpts(is_show=True),toolbox_opts=opts.ToolboxOpts(is_show=True))
)# 渲染图表
radar.render("hot_dog_places.html")

上述代码使用Pyecharts库绘制历年大胃王比赛前三名成绩的雷达图，主要流程为：读取CSV文件`hot-dog-places.csv`，提取列名作为年份维度，前三行数据分别作为三个参赛选手（数据系列）的成绩。动态生成雷达图的维度（年份）及最大值范围，每个年份的最大值取三个系列对应成绩的最大值加10，确保数据点完全显示。创建雷达图实例，依次添加三个数据系列并指定不同颜色，增强区分度；设置全局配置项，包括标题、图例和工具箱（支持缩放、保存等交互功能）。将图表渲染为HTML文件，可通过浏览器查看交互式雷达图，直观比较不同选手在各年份的成绩表现及波动趋势。代码简洁高效，充分利用Pyecharts的交互特性，适合展示多维度时间序列数据的对比关系。

八、总结

图表类型	维度 / 变量数	数据类型	核心功能	典型场景
散点图	2 维	连续变量	观察双变量相关性	身高与体重的关系
气泡图	3 维（X+Y + 大小）	连续变量	双变量 + 权重对比	城市人口、GDP、面积综合比较
相关系数矩阵图	≥3 维	连续变量	全变量对相关性分析	金融指标相关性筛选
二维密度图	2 维	连续变量	数据分布密度展示	用户年龄与消费金额的分布热点
平行坐标图	≥3 维	混合变量	高维数据模式识别	鸢尾花多特征分类分析
桑基图	流数据（源 + 目标）	节点 + 流量（数值）	流程流向与守恒关系	能源生产 - 转换 - 消费路径
雷达图	3-6 维	连续变量（归一化）	多维指标综合对比	企业竞争力多维度评估