当前位置：首页 > ai >正文

【机器学习入门】5.2 回归的起源——从身高遗传到线性模型的百年演变

ai 2025/9/3 13:17:32

提到 “回归”，很多刚入门的同学会觉得它是个抽象的数学概念，但你可能想不到，这个术语的诞生，竟然源于 19 世纪一位生物学家对 “身高遗传” 的研究。回归分析从 “观察生物现象” 出发，逐步发展成机器学习中预测连续值的核心工具，这背后藏着一段有趣的科学史。

这篇文章会沿着 “历史脉络” 展开，从 “回归的提出者（高尔顿）” 讲起，详细拆解他的身高遗传实验、“向均值回归” 现象的发现、“回归” 术语的由来，再到线性回归模型的雏形，让你不仅懂 “回归是什么”，更懂 “它从哪里来”，全程贴合入门认知，不堆砌复杂公式，用生活化的例子还原这段科学历程。

一、回归的 “创始人”：弗朗西斯・高尔顿（Sir Francis Galton）

要讲回归的起源，必须先认识一个人 ——弗朗西斯・高尔顿（1822-1911），英国著名的生物学家、统计学家，也是 “进化论之父” 达尔文的表弟。

高尔顿的研究兴趣非常广泛，从气象学到遗传学，但让他与 “回归” 结缘的，是他对 “遗传规律” 的探索 ——19 世纪末，他一直困惑一个问题：
“如果父母身高很高，他们的孩子会不会越来越高？如果父母身高很矮，孩子会不会越来越矮？长此以往，人类的身高会不会出现‘极端分化’（要么特别高，要么特别矮）？”

为了回答这个问题，他做了一项划时代的研究，这也成为 “回归分析” 的起点。

二、关键实验：身高遗传的 “向均值回归” 现象

高尔顿没有停留在猜想，而是通过 “数据收集 + 分析” 验证自己的疑问，整个实验过程清晰且严谨，即使放在今天看，也符合科学研究的逻辑。

2.1 实验第一步：收集数据 —— 几百个家庭的身高记录

高尔顿联合助手，收集了近 1000 个家庭的身高数据，涵盖父母和子女（每个家庭至少包含 1 位父母和 1 位成年子女）。为了简化分析，他做了两个关键处理：

统一 “父母身高” 计算方式：将 “父亲身高” 和 “母亲身高 ×1.08”（当时认为母亲身高需换算成 “等效父亲身高”，避免性别差异影响）取平均值，得到 “父母平均身高”（记为x）；
聚焦 “成年子女身高”：只统计子女成年后的身高（记为y），避免年龄对身高的影响。

最终，他得到了一组 “父母平均身高 - 子女身高” 的配对数据，比如（父母平均 72 英寸，子女 70 英寸）、（父母平均 62 英寸，子女 64 英寸）等（注：1 英寸≈2.54 厘米，当时英国常用英寸作为身高单位）。

2.2 实验第二步：分析数据 —— 意外发现 “向均值回归”

高尔顿将收集到的数据绘制成 “散点图”（横轴是父母平均身高x，纵轴是子女身高y），然后观察数据的分布规律，结果却出乎他的意料：
身高并没有出现 “极端分化”，反而呈现 “向均值靠拢” 的趋势—— 这就是后来被称为 “向均值回归（Regression to the Mean）” 的核心现象。

我们用具体数据举例，更直观理解这个现象（当时英国成年男性的平均身高约为 68 英寸）：

高个子父母组：父母平均身高 72 英寸（比均值高 4 英寸），他们的子女平均身高约为 70 英寸（比均值高 2 英寸）—— 子女比父母矮，向均值靠拢；
矮个子父母组：父母平均身高 62 英寸（比均值低 6 英寸），他们的子女平均身高约为 64 英寸（比均值低 4 英寸）—— 子女比父母高，也向均值靠拢；
中等身高父母组：父母平均身高 68 英寸（等于均值），他们的子女平均身高也接近 68 英寸 —— 基本稳定在均值附近。

高尔顿在论文中描述这个现象时说：“身高的遗传就像被一根‘无形的线’拉着，极端值总会向平均水平回归，这让人类身高在长期中保持稳定，不会出现极端分化。”

2.3 “回归” 术语的诞生：从 “Regression” 到中文翻译

高尔顿在 1886 年发表的《遗传的身高向均值回归》论文中，第一次使用 “Regression” 这个词来描述上述现象 ——“Regression” 在拉丁语中本意是 “回到之前的状态”，在这里特指 “子女身高回到人类平均身高的状态”。

后来，这个术语被统计学家沿用，并逐步推广到更广泛的领域：只要数据呈现 “极端值向均值靠拢” 的规律，都可以称为 “回归现象”；而用于分析这种现象的数学方法，就被称为 “回归分析”。

到了 20 世纪，回归分析传入中国，“Regression” 被翻译成 “回归”，既保留了 “回到均值” 的核心含义，又简洁易懂，一直沿用至今。

三、从 “现象” 到 “模型”：线性回归的雏形

高尔顿没有止步于发现 “向均值回归” 现象，他进一步思考：“父母身高和子女身高之间，是否存在可量化的数学关系？能不能用一个公式，根据父母身高预测子女身高？”

这一步，他从 “生物学家” 变成了 “统计学家”，也为后来的 “线性回归模型” 奠定了基础。

3.1 拟合 “线性预测线”：找到身高遗传的数学规律

高尔顿将 “父母平均身高x” 和 “子女身高y” 的散点图放在坐标系中，发现这些点虽然分散，但整体呈现 “线性趋势”—— 可以用一条直线来近似描述两者的关系。

他通过当时的 “最小二乘法”（一种让直线与散点 “距离最近” 的数学方法），拟合出了第一条 “身高遗传预测线”，对应的公式（以英寸为单位）为：y=33.73+0.516x

我们来拆解这个公式的含义（入门阶段不用纠结计算细节，重点看物理意义）：

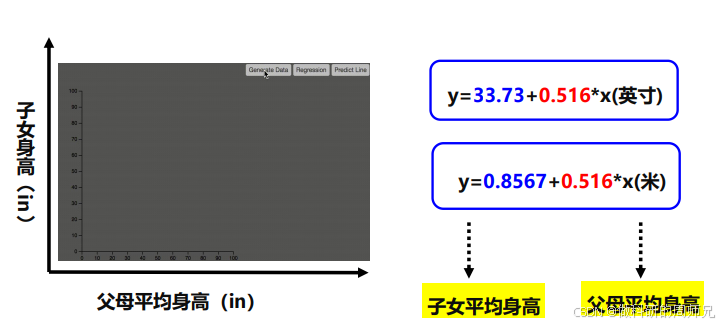
x：父母平均身高（单位：英寸）；
y：预测的子女身高（单位：英寸）；
斜率 0.516：表示 “父母身高每增加 1 英寸，子女身高平均增加 0.516 英寸”—— 这体现了遗传的 “传递强度”，小于 1 说明子女身高不会像父母那样极端，符合 “向均值回归” 规律；
截距 33.73：表示 “当父母平均身高为 0 英寸（极端情况）时，子女身高的基础值”—— 主要用于调整公式的整体水平，让预测更贴合实际数据。

例子：用公式预测子女身高

假设一对父母的平均身高是 72 英寸（高个子父母），代入公式：y=33.73+0.516×72=33.73+37.152=70.882英寸
约等于 71 英寸，比父母平均身高 72 英寸矮，符合 “向均值回归”（均值 68 英寸）的规律，和高尔顿观察到的现象完全一致。

3.2 单位换算：从英寸到米的适配

随着国际单位制的推广，身高单位逐渐从 “英寸” 改为 “米”，高尔顿的公式也被调整为米的版本（保持数学关系不变）：y=0.8567+0.516x

其中：

x：父母平均身高（单位：米）；
y：预测的子女身高（单位：米）；
斜率仍为 0.516：说明 “遗传传递强度” 与单位无关，是身高遗传的固有规律；
截距 0.8567：对应英寸公式的 33.73 英寸（33.73×2.54≈85.67 厘米 = 0.8567 米）。

例子：米单位下的预测

父母平均身高 1.83 米（约 72 英寸），代入公式：y=0.8567+0.516×1.83≈0.8567+0.944≈1.80米
约 1.80 米，比父母平均身高 1.83 米矮，同样符合 “向均值回归” 规律（人类平均身高约 1.75 米）。

3.3 回归分析的 “进化”：从身高到更广泛的预测

高尔顿的身高遗传研究，本质上是 “用线性关系描述两个变量的预测关系”—— 这正是后来 “线性回归” 的核心逻辑。随着统计学的发展，回归分析逐步突破了 “身高遗传” 的局限，推广到更多领域：

经济学家用回归分析预测 “GDP 与就业率的关系”；
农学家用回归分析预测 “施肥量与农作物产量的关系”；
医生用回归分析预测 “血压与年龄的关系”；
到了机器学习时代，回归分析进一步升级，成为 “预测连续值” 的核心模型（如房价预测、销量预测）。

可以说，高尔顿当年的一个简单实验，开启了一门影响深远的统计与机器学习分支。

四、回归起源的核心启示：对入门学生的 3 点启发

了解回归的起源，不仅是 “学历史”，更能帮你理解回归分析的本质，避免陷入 “只记公式不懂原理” 的误区。对入门学生来说，有 3 点关键启示：

4.1 回归的本质：不是 “倒退”，而是 “规律”

很多人看到 “回归” 就以为是 “回到过去”，其实不然 —— 回归的核心是 “数据的统计规律”：极端值总会向均值靠拢，这是一种自然的统计现象，不是 “倒退”，而是 “稳定” 的体现。
比如考试成绩：某次考 100 分（极端高分）的同学，下次可能考 90 分（向班级均值靠拢）；某次考 50 分（极端低分）的同学，下次可能考 60 分 —— 这不是 “退步” 或 “进步”，而是回归规律的体现。

4.2 线性回归的初心：用简单模型描述复杂关系

高尔顿拟合的 “身高预测线”，是最简单的线性模型 —— 只用一个一次函数，就描述了父母身高与子女身高的关系。这告诉我们：好的模型不一定复杂，能准确描述规律的简单模型，往往更有价值。
入门阶段学习线性回归，就是要掌握 “用简单线性关系解决预测问题” 的思维，这是后续学习复杂模型（如多项式回归、神经网络）的基础。